分治法
分治法的核心
- 分:将一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题
- 治:最后的子问题,可以很容易的直接求解
- 合:所有子问题的解合并起来就是原问题的解
分治法的特征
- 问题的规模缩小到一定的程度就可以容易地解决
- 问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质
- 利用该问题分解出的子问题的解可以合并为该问题的解
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
第一条特征:是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加
第二条特征:是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用
第三条特征:是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法
第四条特征:涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好
分治法例题
01. 快速指数
求 ,base为底数,a为指数。
基本思想:对分治:
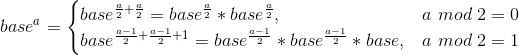
def fast_power(base, a): # 指数为0返回1 if a == 0: return 1.0 # 指数为负数 elif a < 0: return 1 / fast_power(base, -a) # 指数为奇数 elif a % 2: return fast_power(base * base, a // 2) * base # 指数为偶数 else: return fast_power(base * base, a // 2) print(fast_power(2, 5)) # 32
02. 搜索峰值
列表没有重复值,但可能存在多个峰值,返回任意一个峰值的index.
你可以想象成 num[0] = num[n] = -∞, 第一位和最后一位为负无穷
def search_peak(alist, start, end): if start == end: return start if start + 1 == end: if alist[start] > alist[end]: return start return end mid = start + (end - start) // 2 # 如果当前值大于前一个值,并且当前值大于后一个值,则当前值是峰值 if alist[mid - 1] < alist[mid] and alist[mid + 1] < alist[mid]: return mid # 如果前一个值大于当前值,并且当前值大于后一个值,呈下降趋势,前方有峰值,否则后方有峰值 elif alist[mid - 1] > alist[mid] and alist[mid] > alist[mid + 1]: return search_peak(alist, start, mid-1) else: return search_peak(alist, mid + 1, end) alist = [1, 3, 5, 100, 63, 32, 60, 70, 23, 12, 2, 21, 32, 45, 39, 36,11] print(search_peak(alist, 0, len(alist) - 1)) # 7
03. 在有序列表中找多余元素
给定两个排好序的列表。这两个数组只有一个不同的地方:
在第一个数组某个位置上多一个元素。请找到这个元素的索引位置。
def find_extra(lst1, lst2): index = len(lst2) left, right = 0, len(lst2) - 1 while left <= right: mid = left + (right - left) // 2 # 如果中间元素相同,则表示多余元素在后面,否则在前面 if lst1[mid] == lst2[mid]: left = mid + 1 else: index = mid right = mid - 1 return index lst1 = [3, 5, 7, 9, 10, 11, 13] lst2 = [3, 5, 7, 9, 11, 13] print(find_extra(lst1, lst2)) # 4
04. 最大子序列和
在一个一维数组中找到连续的子序列,且这个子序列的加和值最大。
例如,一位数组序列为 [−2, 1, −3, 4, −1, 2, 1, −5, 4]
则这个序列对应的加和值最大的子序列为[4, −1, 2, 1], 其加和值为6.
解决思路:
现将序列等分为左右两份,则最大子列只可能出现在三个地方:
- 整个子序列出现在左半部分
- 整个子序列出现在右半部分
- 整个子序列跨越中间边界
import sys # O(nlogn) def sub_list(alist, left, right): if left == right: return alist[left] mid = left + (right - left) // 2 # 左边序列的最大和 left_sub = sub_list(alist, left, mid) # 右边序列的最大和 right_sub = sub_list(alist, mid + 1, right) # 中间序列的最大和 mid_sub = max_crossing(alist, left, mid, right) # 返回最大值 return max(left_sub, right_sub, mid_sub) def max_crossing(alist, left, mid, right): sum = 0 # sys.maxsize int类型最大值: 9223372036854775807 left_sum = -sys.maxsize # 从中间到左边求和 for i in range(mid, left - 1, -1): sum += alist[i] if sum > left_sum: left_sum = sum sum = 0 right_sum = -sys.maxsize # 从中间到右边求和 for i in range(mid + 1, right + 1): sum += alist[i] if sum > right_sum: right_sum = sum return left_sum + right_sum alist = [-2, 1, -3, 4, -1, 2, 1, -5, 4] sum = sub_list(alist, 0, len(alist) - 1) print(sum) # 6
动态规划简单解法:

# O(n) def sub_list(alist): result = -sys.maxsize local = 0 for i in alist: local = max(local + i, i) result = max(result, local) return result alist = [-2, 1, -3, 4, -1, 2, 1, -5, 4] sub_list(alist) # 6
05. 计算逆序对
对数组做逆序对计数—距离数组的排序结果还有“多远”。如果一个数组已经排好序(升序),那么逆序对个数为0;
如果数组是降序排列的,则逆序对个数最多。
在形式上,如果有两个元素a[i], a[j],如果a[i] > a[j] 且 i < j,那么a[i], a[j]构成一个逆序对。
例如序列[2, 4, 1, 3, 5] 有三个逆序对,分别是(2, 1), (4, 1), (4, 3)
解决思路:
利用归并排序,只要是左边大于右边就有逆序对
# 归并排序 def merge(left_list, right_list): i, j = 0, 0 result_list = list() # 定义一个计数元素 inv_count inv_count = 0 while i < len(left_list) and j < len(right_list): if left_list[i] < right_list[j]: result_list.append(left_list[i]) i += 1 # 只要right>left则是逆序对,inv_count加len(left_list)-i elif left_list[i] > right_list[j]: result_list.append(right_list[j]) j += 1 inv_count += len(left_list) - i result_list += left_list[i:] result_list += right_list[j:] return result_list, inv_count def count_Inversions(alist): if len(alist) <= 1: return alist, 0 mid = len(alist) // 2 left_list, left_inv = count_Inversions(alist[:mid]) right_list, right_inv = count_Inversions(alist[mid:]) result, count = merge(left_list, right_list) count += left_inv + right_inv return result, count alist = [2, 4, 1, 3, 5] print(count_Inversions(alist)) # [1, 2, 3, 4, 5], 3
以上是一些例题!
~>.<!
