二叉堆可以被看作是一个数组,也可以简单的看作是一个近似的完全二叉树,二叉堆有最大堆和最小堆,分别具有堆的性质:最大堆的某个结点的值最多与其父结点一样大,最小堆则是某个结点的值最多与其父结点一样小。所以最大堆中最大的结点永远是根结点,最小堆中最小的结点永远是根节点。
既然二叉堆是一种数据结构,就有其支持的操作(这里以最小堆为例):
- make_heap:建立一个空堆,或者把数组中元素转换成二叉堆。
- insert:插入元素。
- minimun:返回一个最小数。
- extract_min:移除最小结点。
- union:合并堆
make_heap
先给一组数{27,17,3,16,13,10,1,5,7}输入数组,数组下标从0开始。然后我们画出这棵树:
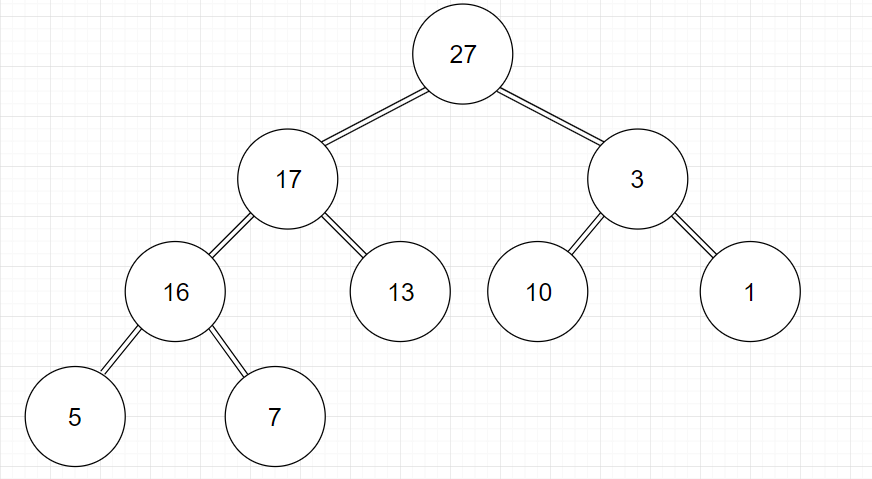
然后根据近似满二叉树的性质,有n个结点,[n/2]+1,[n/2]+2,……,n都是叶结点。然后可以通过对除了叶结点以外的结点i(0到n/2)进行一次下滤的操作,若儿子结点有小于结点i的结点,将儿子结点中最小者与结点i交换,再与交换后的位置的儿子结点继续比较,直到小于儿子结点或者为叶结点为止。遍历完,就得到最小堆。 时间复杂度建立空堆O(1),立地建堆O(n)。
图示
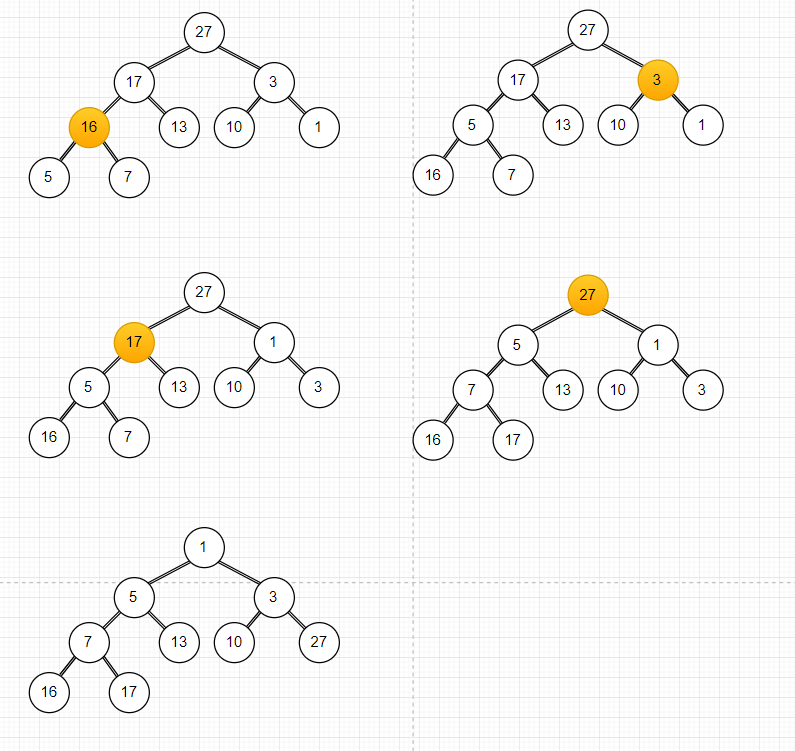
代码实现
1 //维护堆 2 void max_heapify(int *a, int i) { 3 int l = 2 * i + 1; 4 int r = 2 * i + 2; 5 int largest; 6 if (a[l] != -1 && a[l] < a[i]) largest = l; 7 else largest = i; 8 if (a[r] != -1 && a[r] < a[largest]) largest = r; 9 if (largest != i) { 10 swap(a[i], a[largest]); 11 max_heapify(a, largest); 12 } 13 } 14 //建堆 15 void make_heap(int *a, int n) { 16 for (int i = n / 2; i >= 0; i--) max_heapify(a, i); 17 }
insert
对于插入操作,首先将元素push到数组尾部,然后将其进行上滤操作,也就是将其与父结点比较,如果小于父结点就交换,直到大于等于父结点或者到达根。时间复杂度为O(logn)
举个例子:在{1,5,3,7,13,10,27,16,17}中插入4。
图示
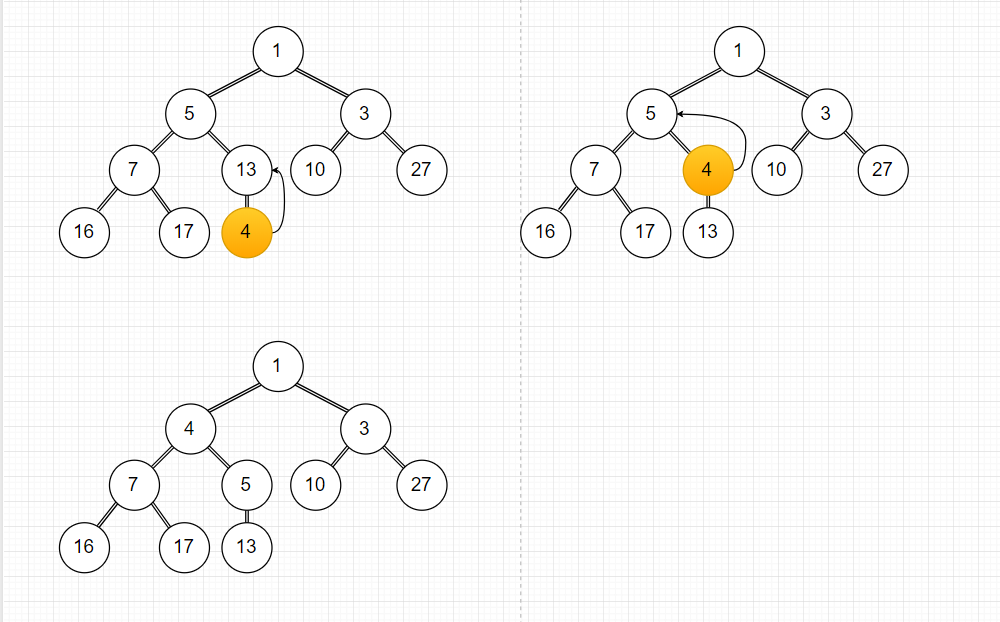
代码实现
1 //n是数组长度 2 void insert(int *a, int num, int &n) { 3 a[n++] = num; 4 for (int i = n - 1; i >= 0; i = (i - 1) / 2) { 5 if (a[i] < a[(i - 1) / 2]) swap(a[i], a[(i - 1) / 2]); 6 else break; 7 } 8 }
minimun
返回最小数,对于最小堆来说返回根即可。时间复杂度O(1)
代码实现
1 int minimun(int *a) { 2 return a[0]; 3 }
extract_min
移除最小顶点,也就是最小堆的根,此时需要将堆最后一个叶节点摘下替换掉根,这样不会破坏近似满二叉树的结构,然后从上至下更新堆,维护堆的性质。时间复杂度O(logn)
图示
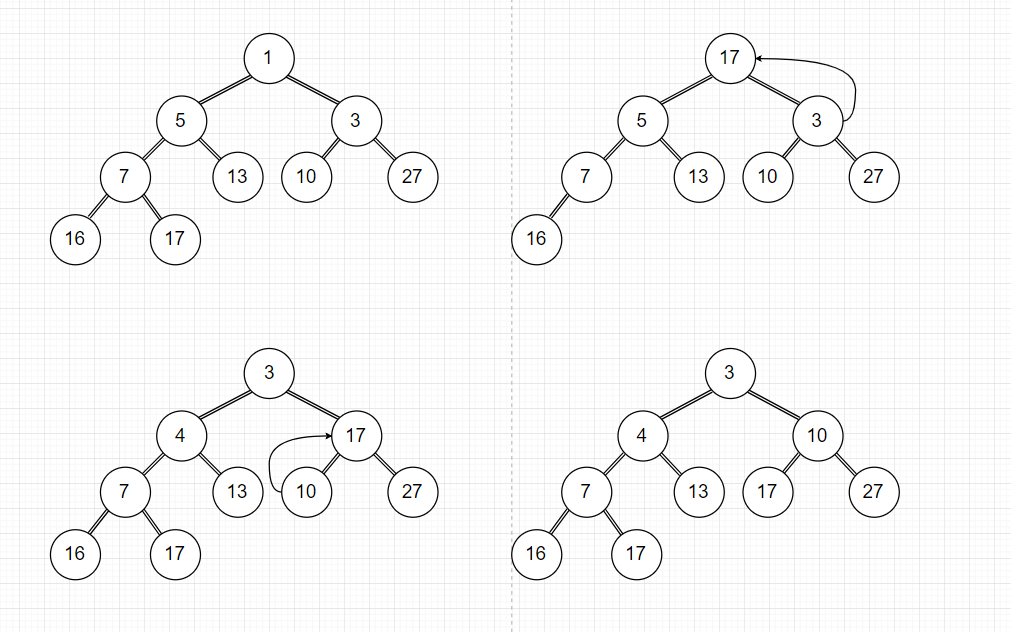
代码实现
1 void extract_min(int *a, int &n) { 2 a[0] = a[n - 1]; 3 n--; 4 max_heapify(a, 0); 5 }
union
合并堆的话其实就相当于把两个堆数组合并,然后重新建堆。所以时间复杂度也是线性的,为O(n)。
代码实现
1 void Union(int *a, int *b, int &n, int &m) { 2 for (int i = 0; i < m; i++) { 3 a[n++] = b[i]; 4 } 5 m = 0; 6 memset(b, -1, sizeof(b)); 7 for (int i = n / 2; i >= 0; i--) max_heapify(a, i); 8 }
这里就说完了二叉堆,下一篇在随便说说堆中的二项堆。