OpenCV_图像平滑

1、均值滤波

与一维信号一样，我们可以对图像滤波，如高通滤波和低通滤波。高通滤波可以使我们找到图片的边界，低通滤波可以使得图像平滑，去除掉图像中的噪声，模糊图像。OpenCV提供了cv.filter2d()函数，使用该函数以一个卷积核对图像卷积可以得到滤波后的图片。以下面的这个卷积核为例:

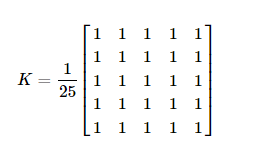
这是一个5x5的卷积核，使用这个核在图像上进行卷积操作时，卷积核上的每一个元素与图像上对应的像素点值相乘并累加，最后取平均值，可以将这一个卷积核看作是对图像上被卷积核覆盖的小区域求像素均值，并用这个均值代替位于区域中心像素点值。示例代码：

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('hahaha.jpg')
b,g,r=cv.split(img)
img=cv.merge([r,g,b])
kernel = np.ones((5,5),np.float32)/25
dst = cv.filter2D(img,-1,kernel)
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('Averaging')
plt.xticks([]), plt.yticks([])
plt.show()

程序结果:

从结果中可以看到，图像变得“模糊”了。

2、高斯模糊

如果将上面代码中的卷积核换成高斯卷积核，那么这个过程就是高斯模糊。高斯核内的元素服从二维高斯分布，即中心的值最大，随着到中心距离的增加，权重逐渐减小。

二维高斯函数的数学表达式为：

其图像如下所示：

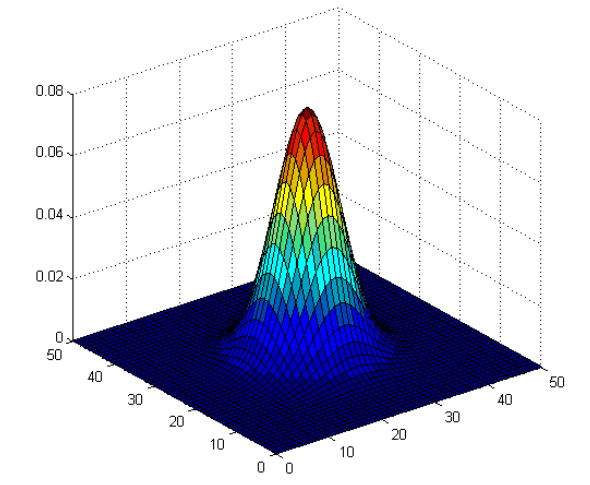
二维高斯函数是钟形曲面。越接近中心，取值越大，越接近边缘，取值越小。

在高斯卷积核中，假定核的大小为2k+1，那么在卷积核中位置为（i，j）处的权重大小为：

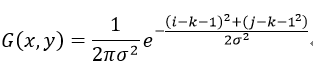
σ是标准差，假定σ=1，k=3，经过上述计算可以得到下面矩阵：

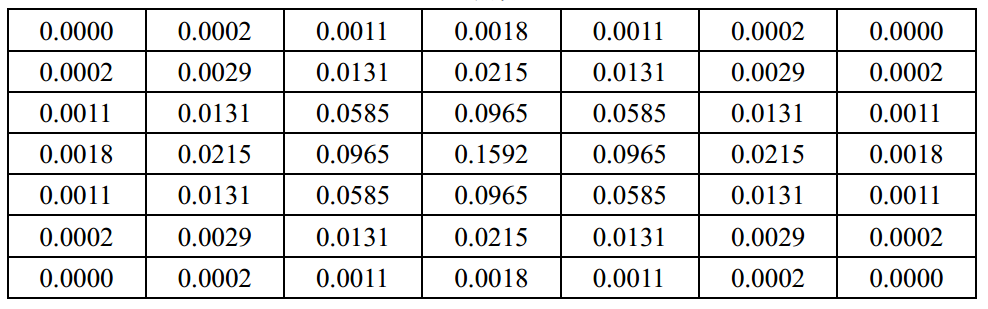
由于程序在计算整数时效率会更快，并且像素值只能是一系列连续的整数（0-255），所以以小数来计算加权和的平均值是没有意义的，因此，我们将上面的卷积核整数化，全部除以左上角元素得到如下模板：

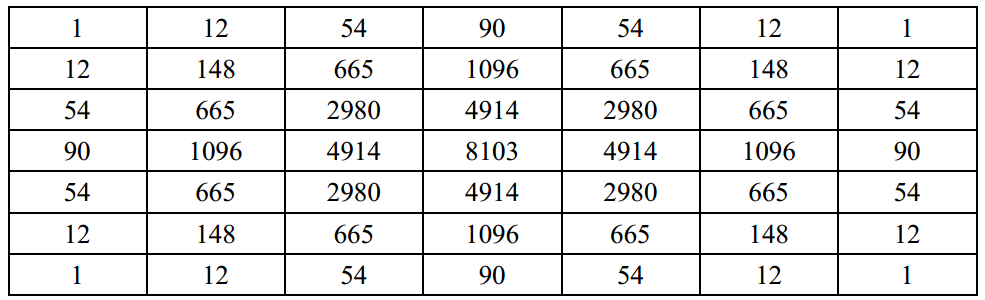
最后再在前面乘以矩阵内所有元素和的倒数即可。从二维高斯函数的公式可以看出，卷积核内的权重值其实是由标准差σ决定的，权重值按照一定的比例变化。特别地，当σ²=1/2ln2时，权重值以2为倍数递增，中心处的权重最大。

高斯卷积核其实是一个低通滤波器，它能够使得图像变得平滑。在OpenCV中，使用函数cv2.GaussianBlur()来实现高斯滤波，函数定义如下：

dst=cv.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])

src:源图像；ksize:卷积核的尺寸，即长和宽，长和宽可以不等，但必须是正奇数；sigmaX:x方向的标准差；sigmaY：y方向上的标准差，如果sigmaY等于0，那么令其等于sigmaX，如果二者都等于0，那么程序将会自动计算sigmaX和sigmaY。

示例代码：

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('hahaha.png')
b,g,r=cv.split(img)
img=cv.merge([r,g,b])
dst = cv.GaussianBlur(img,(5,5),0)
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('GaussianBlur')
plt.xticks([]), plt.yticks([])
plt.show()

程序结果：

原始图片掺杂了很多噪音，经过高斯滤波后，可以看见图片中的噪声被去除了一部分，图片变得更加平滑。

3、中值模糊

这个滤波器将卷积核范围内的像素值经过排序然后取中值作为滤波后像素点的值。相比于前面两种滤波方式，这种方法取像素点邻域内的值（也可以是该像素点本身）来替代该像素值。中值模糊主要用来去除图像中的椒盐噪声。OpenCV中使用函数cv.medianBlur()来实现中值滤波。该函数的定义如下：dst=cv.medianBlur(src, ksize[, dst])。使用该函数时需要指定源图像，卷积核的尺寸。

示例代码：

img = cv.imread('hahaha.png')
b,g,r=cv.split(img)
img=cv.merge([r,g,b])
dst=cv.medianBlur(img,5)
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('MedianBlur')
plt.xticks([]), plt.yticks([])
plt.show()

程序结果：

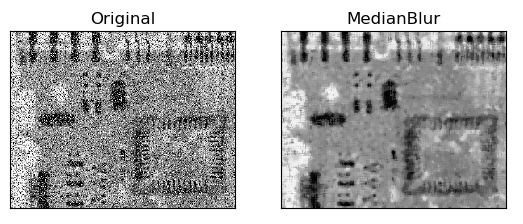
4、双边滤波

上面几种滤波方法在处理图像时没有考虑到一个像素是否位于图像的边界处，因此滤波后的图像边界也模糊掉了，这不是我们想要的。与前述滤波方法相比，双边滤波具有保留图像边界的优点。双边滤波在同时使用空间高斯权重和灰度值相似性高斯权重。空间高斯函数确保只有邻近区域的像素对中心点有影响，灰度值相似性高斯函数确保只有与中心像素灰度值相近的才会被用来做模糊运算。所以这种方法会确保边界不会被模糊掉，因为边界处的灰度值变化比较大。OpenCV中使用函数cv.bilateralFilter来实现双边滤波，函数定义如下：dst=cv.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])

src:源图像；d:卷积核的尺寸（邻域直径）；sigmaColor:灰度相似性高斯函数的标准差；sigmaSpace:空间高斯函数的标准差。

示例代码：

img = cv.imread('hahaha.jpg')
b,g,r=cv.split(img)
img=cv.merge([r,g,b])
dst1=cv.bilateralFilter(img,9,75,75)
dst2=cv.GaussianBlur(img,(5,5),0)
dst3=cv.medianBlur(img,5)
plt.subplot(221),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(dst1),plt.title('bilateralBlur')
plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(dst2),plt.title('GaussianBlur')
plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(dst3),plt.title('medianBlur')
plt.xticks([]), plt.yticks([])
plt.show()

程序结果：

从上面结果可以看到，相较于高斯滤波和中值滤波，双边滤波后的图像边界得以保留，而另外两者的边界均被模糊化了。