动态规划
动态规划问题可以通过通过金矿模型介绍动态规划很好的解释其中的原理,在理论上,动态规划问题的关键点用通俗的语言来说就是,现在有一个大问题,不好解决,为什么呢?因为这个大问题有很多小问题组成,这些小问题之间不是相互独立的,而且是一个是另一个的解决的基础,这就是所谓的子问题重叠,子问题重叠,我们就不能简简单单的通过分治算法来解决问题了,必须得分析其中的相关联因素。
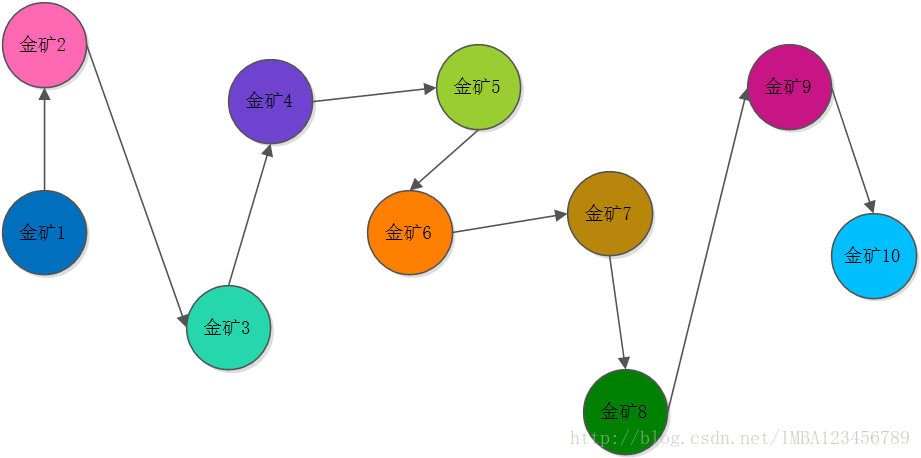
目前的情况是这样的,我们已经知道这个大问题,由很多小问题组成,小问题之间又有相互的关联,就比如说,我们制订了一种方案,这种方案恰好可以通过如图所示的次序
来完成我们的开采,使得人力资源不至于浪费,使用到最大程度的同时,挖到最多的金矿,我们在没有制定方案的时候就已经知道了整个过程的最初和结束状态,而整个行动的过程,就是我们制定决策的过程,在这个过程之中,我们要对问题按照时空特性进行划分阶段,划分后的每个阶段是有序的或者可排序的,即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关,这叫做无后效性 。
现在,我们将问题进了分解,将大问题分解成了小问题,而且对问题划分了阶段,那么我们如何保证我们这样做得到的答案是最优的呢?这就是最优子结构,就是说,如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理,很明显,就拿挖矿模型来说,一座金矿,我们认定的是,要么挖,要么不挖,我们所做的假设只有一种会被国王所采纳,这就满足了子问题独立,一个人的决定对另一个人的决定是没有影响的,所以,我们要么得到在小于总人力的情况下的金矿的最大价值,只能当前第10座金矿的情形下,比较如果不挖掘的(以前挖掘的9座金矿(总人力的情况下))价值和(挖掘第10座金矿+以前挖掘的9座金矿(总人力的情况下-第10座金矿需要消耗的人力))的价值谁更大,我们就采取那种方式,很显然,自信的国王相信,只要他的两个大臣能够回答出正确的答案(对于考虑能够开采出的金子数,最多的也就是最优的同时也就是正确的),再加上他的聪明的判断就一定能得到最终的正确答案。我们把这种子问题最优时母问题通过优化选择后一定最优的情况叫做最优子结构。所以这也是符合最优子结构的,如此而言,动态规划的三个要点,子问题重叠,无后效性,最优子结构就展现在了我们面前。
我们在具体解决问题的时候需要注意的有4点:1.划分阶段:按照问题的时间或空间特征,把问题分为若干个阶段。在划分阶段时,注意划分后的阶段一定要是有序的或者是可排序的,否则问题就无法求解。2.确定状态和状态变量:将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然,状态的选择要满足无后效性。3。确定决策并写出状态转移方程:因为决策和状态转移有着天然的联系,状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策,状态转移方程也就可写出。但事实上常常是反过来做,根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。4.寻找边界条件:给出的状态转移方程是一个递推式,需要一个递推的终止条件或边界条件。一般,只要解决问题的阶段、状态和状态转移决策确定了,就可以写出状态转移方程(包括边界条件)。实际应用中可以按以下几个简化的步骤进行设计:
1.分析最优解的性质,并刻画其结构特征。
2.递归的定义最优解。
3.以自底向上或自顶向下的记忆化方式(备忘录法)计算出最优值。
4.根据计算最优值时得到的信息,构造问题的最优解。
所以,我们的重头戏就是写出状态转移方程,其中我们已经在绿色的部分作出了分析,得到了以下的表达式:
V[i][w]=Max{ V[i-1][w] ,V[i-1][w-w[i]]+p[i]}
其中表达式的含义解释如下:
以0-1背包问题来作解释,欲求前i个物体放入容量为w(kg)背包的最大价值V[i][w]——使用一个数组来存储最大价值,而前i个物体放入容量为w(kg)的背包,又可以转化成前(i-1)个物体放入背包的问题。下面使用数学表达式描述它们两者之间的具体关系。
表达式中各个符号的具体含义。
w:背包的总重量
w[i]:第i个物体的重量
p[i]:第i个物体的价值
V[i][w]:前i个物体放入容量为w的背包的最大价值
V[i-1][w]: 前i-1个物体放入容量为w的背包的最大价值
V[i-1][w-w[i]]:前i-1个物体放入容量为w-w[i]的背包的最大价值
总结:在解决动态规划的问题的时候,我们推理的时候是倒推的,即总最后的结果倒推,我们在满足限制条件的情况下,讲问题分解,分解成,最后一个物品要不要放到背包里,如果放会怎么样,不放又会怎么样,然后就得到了两个子问题,子问题接着又是放或者不放,一直倒退到第一个物品,这样就得到了整个问题的全貌,然后写出了状态转移方程,倒推的目的是要找出来状态转移方程,但是当状态转移方程找出来之后,我们编程的时候,就需要用正推(遍历)的方式来求解问题的最优解,这时候,我们将最优解放在一个数组里面。
具体的代码和解释如下:
public class MyBags
{
/*物品类*/
static class Things
{
/*重量*/
private int weight;
/*价值*/
private int value;
Things(int w, int v)
{
this.weight = w;
this.value = v;
}
public intgetWeight()
{
return weight;
}
public int getValue()
{
return value;
}
}
/*背包总承重*/
private int totalWeight;
/*物品数量*/
private int thingsNumber;
/*总的物品*/
private Things[] things;
/*在放入第i个物体,总重为w时候的背包价值*/
private int[][] values;
private int bestValue;
MyBags(Things[] t, int w)
{
this.things = t;
this.totalWeight = w;
this.thingsNumber =t.length;
if (values == null)
{
values = newint[thingsNumber + 1][totalWeight + 1];
}
}
public int getValue()
{
//对背包承重进行遍历
for (int j = 0; j<= totalWeight; j++)
{
//对物品进行遍历
for (int i = 0; i<= thingsNumber; i++)
{
if (i == 0 ||j == 0)
{
values[i][j] = 0;
} else
{
/*此时有两种情况,要么放,要么不放
* 为什么放?--->因为要取得最大的价值!--->在总重w情况下,前i-1个物品价值
* 和总重w-w[i]情况下前i-1个物品加上第i个物品的价值谁大。
* 为什么不放?----因为已经放不下了!--->最大价值在前面的i-1个物品中诞生!*/
if (j< things[i - 1].getWeight()) //放不下
{
values[i][j] = values[i - 1][j];
} else
{
values[i][j] = Math.max(values[i - 1][j], values[i - 1][j - things[i -1].getWeight()] + things[i - 1].getValue());
}
}
}
}
bestValue =values[thingsNumber][totalWeight];
return bestValue;
}
public static voidmain(String[] args)
{
Things[] things = newThings[]{new Things(4, 5), new Things(3, 6), new Things(7, 10)};
int totalWeight = 8;
MyBags mb = newMyBags(things, totalWeight);
int best =mb.getValue();
System.out.println(best);
}
} 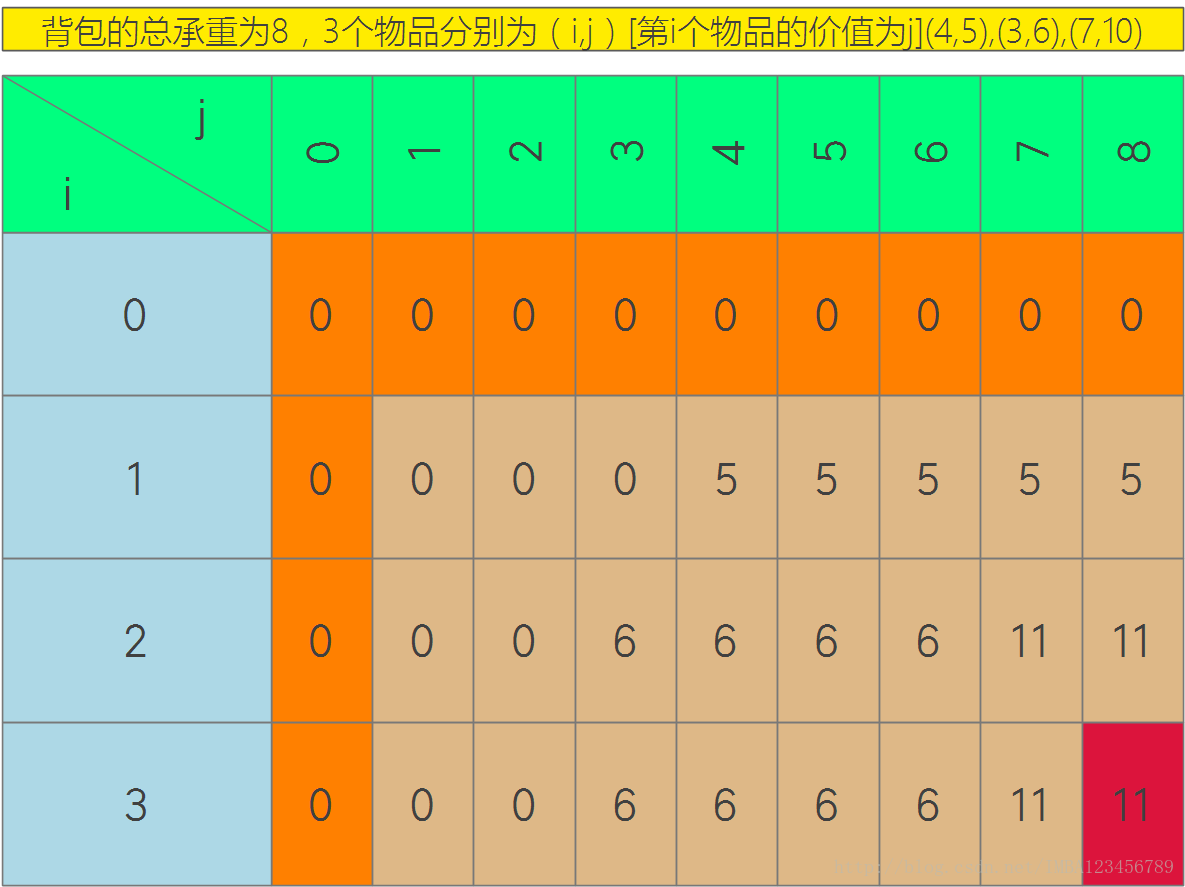
这幅图标表达的含义如下,当i=2,j=3时,当包的承重为3时,在目前,只装1,2物品的情况下,我们可以得到的最大值是6,这恰好表明了,我们在分析问题的时候是从最后开始,需要得到最大的值,而真正解决问题的时候,我们是从第一个物品开始,不断去试探,那个才符合我们的最终想要的意图,所以说在分析和解决问题时候的两种刚好相反的思路才是我们需要注意和关切的。此处的i=0和j=0(橘黄色表示)只是为了满足数组下标从0开始这个习惯,去除也是可以的,此处加上是为了方便于代码的理解。
例子引用:通过金矿模型介绍动态规划
转载请注明出处,谢谢。