数学建模

追逐问题1

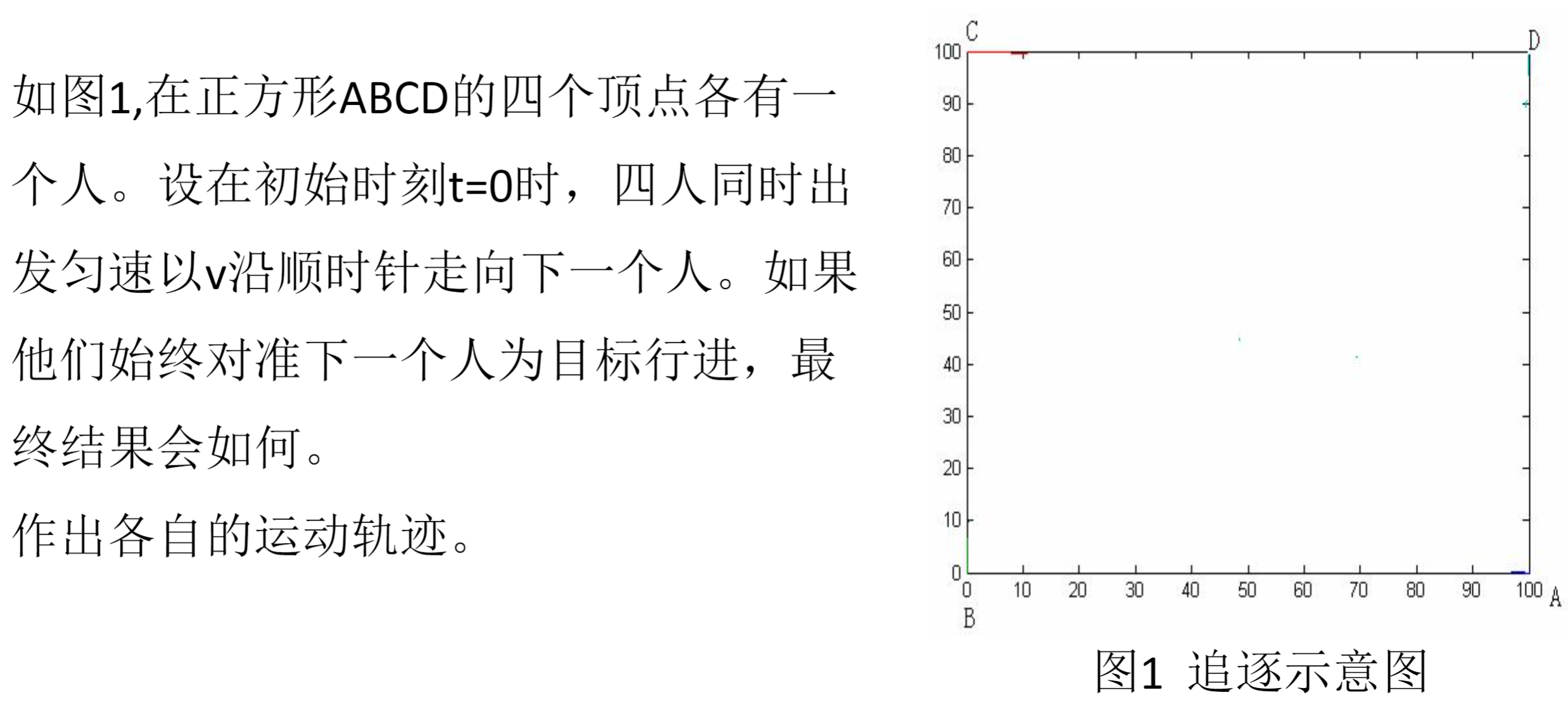
用离散值近似拟合连续值，可以用于快速理解题意。

import numpy as np
from matplotlib import pyplot as plt
import math

n = 240
x = np.zeros(shape=(4,n))
y = np.zeros(shape=(4,n))

x[0,0] = 100
y[0,0] = 0
x[1,0] = 0
y[1,0] = 0
x[2,0] = 0
y[2,0] = 100
x[3,0] = 100
y[3,0] = 100

def compute_direct(i,j):
    i2 = (i+1)%4
    cos_theta = (x[i2,j]-x[i,j]) / math.sqrt((x[i2,j]-x[i,j]) ** 2 + (y[i2,j]-y[i,j]) ** 2)
    sin_theta = (y[i2,j]-y[i,j]) / math.sqrt((x[i2,j]-x[i,j]) ** 2 + (y[i2,j]-y[i,j]) ** 2)
    return cos_theta, sin_theta


def move(i,j,v,dt):
    cos_theta, sin_theta = compute_direct(i,j)
    x[i,j+1] = x[i,j] + v * dt * cos_theta
    y[i,j+1] = y[i,j] + v * dt * sin_theta


dt = 0.05
v = 10

for _ in range(n-1):
    for i in range(4):
        move(i,_,v,dt)


plt.plot(x[0],y[0],'red', label='A')
plt.plot(x[1],y[1],'green', label='B')
plt.plot(x[2],y[2],'blue', label='C')
plt.plot(x[3],y[3],'black', label='D')
plt.legend()
plt.show()

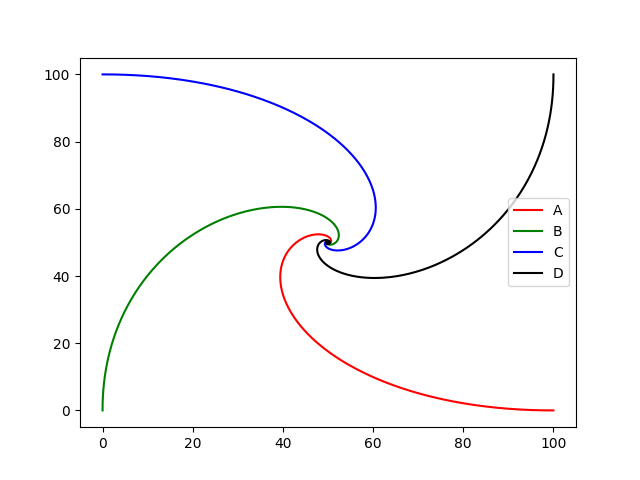
追逐问题2

import math
from matplotlib import pyplot as plt
import numpy as np

dt = 0.001 # h
max_time = 100000
threshold = 0.1

x = np.zeros(shape=(2, max_time))
y = np.zeros(shape=(2, max_time))
v = [8, 12]
x[0,0] = 10

def move(i): # i * dt
    x[0, i+1] = x[0, i]
    y[0, i+1] = y[0, i] + dt * v[0]
    cos_theta = (x[0, i] - x[1, i]) / math.sqrt((x[0, i+1] - x[1,i]) ** 2 + (y[0, i+1] - y[1,i]) ** 2)
    sin_theta = (y[0, i] - y[1, i]) / math.sqrt((x[0, i+1] - x[1,i]) ** 2 + (y[0, i+1] - y[1,i]) ** 2)
    x[1, i+1] = x[1, i] + dt * v[1] * cos_theta
    y[1, i+1] = y[1, i] + dt * v[1] * sin_theta

def is_meet(i):
    return math.sqrt((x[0, i]- x[1, i]) ** 2 + (y[0, i]- y[1, i]) ** 2)  < threshold

cur_time = 0

while  cur_time < max_time-1 and not is_meet(cur_time):
    move(cur_time)
    cur_time += 1


print('meet time = {0} hours'.format(dt * cur_time))
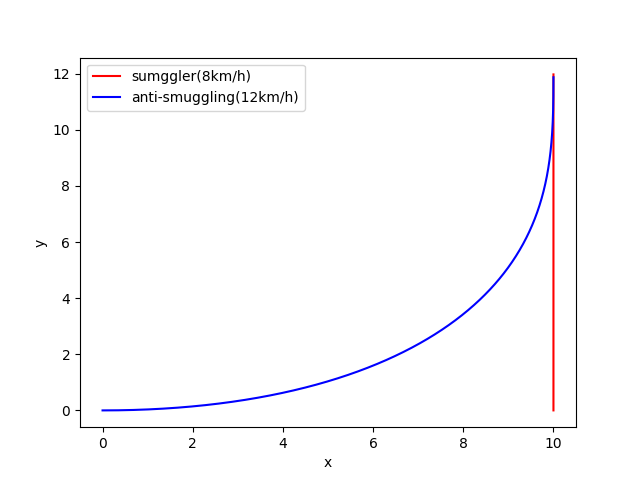
plt.plot(x[0][:cur_time], y[0][:cur_time], 'red', label= 'sumggler(8km/h)')
plt.plot(x[1][:cur_time], y[1][:cur_time], 'blue', label='anti-smuggling(12km/h)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()