DIV1 250pt
题意:称string s是vector<string> words的ordered superstring,如果它满足:存在一个数列{x0, x1, x2...xm}(m = words.size()),使得words[i]与s中从xi开始的,长度为words[i].size()的字符串相同,且x0 <= x1 <= x2 <= ... <= xm。
给定words,求最短的ordered superstring。words.size() <= 50,words[i].size() <= 50。
解法:模拟题。由于使用指针比较易错加上我代码太不稳于是wa了。。。。
tag:simulation

1 // BEGIN CUT HERE 2 /* 3 * Author: plum rain 4 * score : 5 */ 6 /* 7 8 */ 9 // END CUT HERE 10 #line 11 "OrderedSuperString.cpp" 11 #include <sstream> 12 #include <stdexcept> 13 #include <functional> 14 #include <iomanip> 15 #include <numeric> 16 #include <fstream> 17 #include <cctype> 18 #include <iostream> 19 #include <cstdio> 20 #include <vector> 21 #include <cstring> 22 #include <cmath> 23 #include <algorithm> 24 #include <cstdlib> 25 #include <set> 26 #include <queue> 27 #include <bitset> 28 #include <list> 29 #include <string> 30 #include <utility> 31 #include <map> 32 #include <ctime> 33 #include <stack> 34 35 using namespace std; 36 37 #define clr0(x) memset(x, 0, sizeof(x)) 38 #define clr1(x) memset(x, -1, sizeof(x)) 39 #define pb push_back 40 #define sz(v) ((int)(v).size()) 41 #define all(t) t.begin(),t.end() 42 #define zero(x) (((x)>0?(x):-(x))<eps) 43 #define out(x) cout<<#x<<":"<<(x)<<endl 44 #define tst(a) cout<<a<<" " 45 #define tst1(a) cout<<#a<<endl 46 #define CINBEQUICKER std::ios::sync_with_stdio(false) 47 48 typedef vector<int> vi; 49 typedef vector<string> vs; 50 typedef vector<double> vd; 51 typedef pair<int, int> pii; 52 typedef long long int64; 53 54 const double eps = 1e-8; 55 const double PI = atan(1.0)*4; 56 const int inf = 2139062143 / 2; 57 58 bool ok(string a, string b) 59 { 60 for (int i = 0; i < min(sz(a), sz(b)); ++ i) 61 if (a[i] != b[i]) return 0; 62 return 1; 63 } 64 65 class OrderedSuperString 66 { 67 public: 68 int getLength(vector <string> w){ 69 string s; s.clear(); 70 int idx = 0; 71 for (int i = 0; i < sz(w); ++ i){ 72 int match = sz(s); 73 for (int j = idx; j < sz(s); ++ j) 74 if (ok(string(s.begin()+j, s.end()), w[i])){ 75 match = j; break; 76 } 77 idx = match; 78 if (sz(s) - match < sz(w[i])) 79 s += string(w[i].begin()+sz(s)-match, w[i].end()); 80 } 81 return sz(s); 82 } 83 84 // BEGIN CUT HERE 85 public: 86 void run_test(int Case) { if ((Case == -1) || (Case == 0)) test_case_0(); if ((Case == -1) || (Case == 1)) test_case_1(); if ((Case == -1) || (Case == 2)) test_case_2(); if ((Case == -1) || (Case == 3)) test_case_3(); } 87 private: 88 template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '"' << *iter << "","; os << " }"; return os.str(); } 89 void verify_case(int Case, const int &Expected, const int &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << " Expected: "" << Expected << '"' << endl; cerr << " Received: "" << Received << '"' << endl; } } 90 void test_case_0() { string Arr0[] = {"aaaaaaaaaaabaaaaaaaa", "bac", "aaaabacaaa", "ab", "ba", "a", "ca"}; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[0]))); int Arg1 = 4; verify_case(0, Arg1, getLength(Arg0)); } 91 void test_case_1() { string Arr0[] = {"a","a","b","a"}; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[0]))); int Arg1 = 3; verify_case(1, Arg1, getLength(Arg0)); } 92 void test_case_2() { string Arr0[] = {"abcdef", "ab","bc", "de","ef"}; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[0]))); int Arg1 = 6; verify_case(2, Arg1, getLength(Arg0)); } 93 void test_case_3() { string Arr0[] = {"ab","bc", "de","ef","abcdef"}; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[0]))); int Arg1 = 12; verify_case(3, Arg1, getLength(Arg0)); } 94 95 // END CUT HERE 96 97 }; 98 99 // BEGIN CUT HERE 100 int main() 101 { 102 // freopen( "a.out" , "w" , stdout ); 103 OrderedSuperString ___test; 104 ___test.run_test(-1); 105 return 0; 106 } 107 // END CUT HERE
DIV1 600pt
题意:给3个正整数n1, n2, up,求能被C(n1+n2, n1)整除的,且小等于up的最大正整数。n1,n2 <= 10^9,up <= 10^5。
解法:首先,枚举小等于up的所有数是肯定的。那么现在考虑,对整数k,如何判定它能不能被C(n1+n2, n1)整数。
当数据太大不能被直接表示,又不能用余数间接表示的时候,就考虑它的所有质因子。只用考虑sqrt(k)以内的所有质因子,或者k为质数。
然后,考虑到组合数的特殊性,C(n1+n2, n1) = (n1+n2)! / (n1! * n2!)。所以下面考虑对某个质因子t,如何求n!含有多少个质因子t。
下图为13!含有因子2的个数,一个X代表一个。也即是说,13的阶乘含有因子2的数量为13/2 + 13/(2^2) + 13/(2^3)。
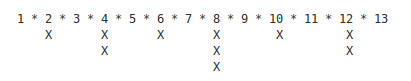
tag:math, number theory, good

1 // BEGIN CUT HERE 2 /* 3 * Author: plum rain 4 * score : 5 */ 6 /* 7 8 */ 9 // END CUT HERE 10 #line 11 "MagicalSpheres.cpp" 11 #include <sstream> 12 #include <stdexcept> 13 #include <functional> 14 #include <iomanip> 15 #include <numeric> 16 #include <fstream> 17 #include <cctype> 18 #include <iostream> 19 #include <cstdio> 20 #include <vector> 21 #include <cstring> 22 #include <cmath> 23 #include <algorithm> 24 #include <cstdlib> 25 #include <set> 26 #include <queue> 27 #include <bitset> 28 #include <list> 29 #include <string> 30 #include <utility> 31 #include <map> 32 #include <ctime> 33 #include <stack> 34 35 using namespace std; 36 37 #define clr0(x) memset(x, 0, sizeof(x)) 38 #define clr1(x) memset(x, -1, sizeof(x)) 39 #define pb push_back 40 #define sz(v) ((int)(v).size()) 41 #define all(t) t.begin(),t.end() 42 #define zero(x) (((x)>0?(x):-(x))<eps) 43 #define out(x) cout<<#x<<":"<<(x)<<endl 44 #define tst(a) cout<<a<<" " 45 #define tst1(a) cout<<#a<<endl 46 #define CINBEQUICKER std::ios::sync_with_stdio(false) 47 48 typedef vector<int> vi; 49 typedef vector<string> vs; 50 typedef vector<double> vd; 51 typedef pair<int, int> pii; 52 typedef long long int64; 53 54 const double eps = 1e-8; 55 const double PI = atan(1.0)*4; 56 const int inf = 2139062143 / 2; 57 const int N = 100005; 58 59 60 class MagicalSpheres 61 { 62 public: 63 int64 gao (int x, int m) 64 { 65 int64 num = 0; 66 int64 tmp = m; 67 while (tmp <= x){ 68 num += x / tmp; 69 tmp *= m; 70 } 71 return num; 72 } 73 74 int divideWork(int n1, int n2, int up){ 75 for (int i = up; i; -- i){ 76 bool ok = 0; 77 int k = i; 78 for (int j = 2; j*j <= k; ++ j) if (k % j == 0){ 79 int t = 0; 80 while (!(k % j)) 81 k /= j, ++ t; 82 if (gao(n1+n2, j) - gao(n1, j) - gao(n2, j) < t) ok = 1; 83 } 84 if (k != 1) 85 if (gao(n1+n2, k) - gao(n1, k) - gao(n2, k) < 1) ok = 1; 86 if (!ok) return i; 87 } 88 return 1; 89 } 90 91 // BEGIN CUT HERE 92 public: 93 void run_test(int Case) { if ((Case == -1) || (Case == 0)) test_case_0(); if ((Case == -1) || (Case == 1)) test_case_1(); if ((Case == -1) || (Case == 2)) test_case_2(); if ((Case == -1) || (Case == 3)) test_case_3(); } 94 private: 95 template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '"' << *iter << "","; os << " }"; return os.str(); } 96 void verify_case(int Case, const int &Expected, const int &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << " Expected: "" << Expected << '"' << endl; cerr << " Received: "" << Received << '"' << endl; } } 97 void test_case_0() { int Arg0 = 1000000000; int Arg1 = 1000000000; int Arg2 = 100000; int Arg3 = 2; verify_case(0, Arg3, divideWork(Arg0, Arg1, Arg2)); } 98 void test_case_1() { int Arg0 = 3; int Arg1 = 3; int Arg2 = 50; int Arg3 = 20; verify_case(1, Arg3, divideWork(Arg0, Arg1, Arg2)); } 99 void test_case_2() { int Arg0 = 4; int Arg1 = 3; int Arg2 = 4; int Arg3 = 1; verify_case(2, Arg3, divideWork(Arg0, Arg1, Arg2)); } 100 void test_case_3() { int Arg0 = 15634; int Arg1 = 456; int Arg2 = 5000; int Arg3 = 4990; verify_case(3, Arg3, divideWork(Arg0, Arg1, Arg2)); } 101 102 // END CUT HERE 103 104 }; 105 106 // BEGIN CUT HERE 107 int main() 108 { 109 // freopen( "a.out" , "w" , stdout ); 110 MagicalSpheres ___test; 111 ___test.run_test(-1); 112 return 0; 113 } 114 // END CUT HERE
