摘自大神博客:
http://www.cnblogs.com/SYCstudio/p/7260613.html
增广路定理+分层图+当前弧优化
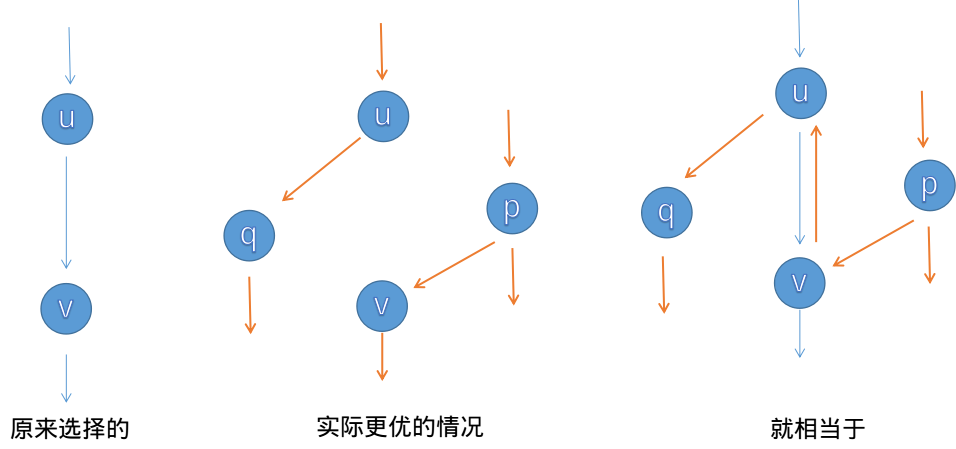
增广路:从源点出发不停的通过dfs出一条路径到汇点(直到无法走到汇点),每次dfs找出路径中最小残量,回溯时都减掉这个最小残量,并且连一条回边(原因如下图 :)
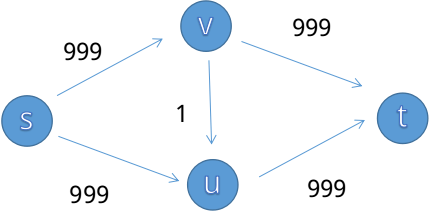
分层图:发现增广图处理下图问题非常耗时(s->v->u->t而不是s->v->t),所以每次dfs前都先用bfs求一次深度dep,且dfs时只允许低深度到高深度
当前弧优化:每次dfs不是从汇点的第一条边开始,而是用cur数组记录u循环到哪条边,以此来加速
上代码:
int n, m, s, t;
struct edge
{
int to, w, nx;
} e[N << 1];
int fi[N];
int ce = 1;
int dep[N];
bool vis[N];
int cur[N];
inline void add(int u, int v, int w)
{
e[++ce] = edge{v, w, fi[u]};
fi[u] = ce;
}
int bfs()
{
me(dep, 0);
queue<int> q;
q.push(s);
dep[s] = 1;//特别注意这里赋值个不为0的数,不然就是死循环!!!
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = fi[u]; ~i; i = e[i].nx)
{
int v = e[i].to;
if (e[i].w && !dep[v])
{
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t];
}
int dfs(int u, int flow)
{
if (u == t)
return flow;
for (int &i = cur[u]; ~i; i = e[i].nx)
{
int v = e[i].to;
if (e[i].w && dep[u] + 1 == dep[v])
{
int di = dfs(v, min(e[i].w, flow));
if (di)
{
e[i].w -= di, e[i ^ 1].w += di;
return di;
}
}
}
return 0;
}
int dinic(int s, int t)
{
int res = 0;
int cnt = 0;
while (bfs())
{
if (++cnt > 20)
break;
For(i, 1, n) cur[i] = fi[i];
while (int di = dfs(s, inf))
res += di;
}
return res;
}
int main()
{
#ifndef ONLINE_JUDGE
file("test");
#endif
me(fi, -1);
sdf(n), sdf(m), sdf(s), sdf(t);
while (m--)
{
int u, v, w;
sdf(u), sdf(v), sdf(w);
add(u, v, w), add(v, u, 0);
}
printf("%d", dinic(s, t));
return 0;
}