摘自大佬文章
https://www.luogu.org/blog/user19027/solution-p3369
维护一个数据结构
1.插入 x 数
2.删除 x 数(若有多个相同的数,因只删除一个)
3.查询 x 数的排名(排名定义为比当前数小的数的个数 +1+1 。若有多个相同的数,因输出最小的排名)
4.查询排名为 x的数
5.求 x 的前驱(前驱定义为小于 x ,且最大的数)
6.求 x 的后继(后继定义为大于 x ,且最小的数)
涉及函数如下:
class Splay{
class node{}
update(x),identify(x),connect(x,f,son),rotate(x),splay(at,to),crepoint(v,father),destroy(x);
find(v),insert(v),push(v),pop(v),rk(v),atrk(x),upper(v),lower(v);
}
代码很长,记住几个感觉:
1.旋转上升
2.每次儿子只篡父亲的位
3.尽全力发挥想象力,做到心中有图
4.定义总根为0节点 #define root e[0].ch[1]
下面开始讲解:
class node{
public:
int v,father;//节点值,父亲
int ch[2];
int sum,recy;//记录自己向下包含多少个元素(不单纯是节点数哦),当前节点重复次数
}e[maxn];
//更新统计总元素数
void update(int x){
e[x].sum=e[e[x].ch[0]].sum+e[e[x].ch[1]].sum+e[x].recy;
}
//判断x是父节点的左节点还是右节点
int identify(int x){
return e[e[x].father].ch[0]==x?0:1;
}
//与父节点连接
void connect(int x,f,son){ //当前节点,父节点,左or右
e[x].father=f;
e[f].ch[son]=x;
}
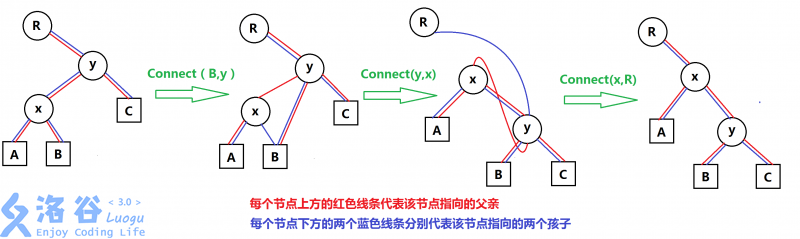
//旋转上升(且只上升一层) 分三步走(自下而上,当前节点为而儿子,孙子->父亲,父亲->儿子,儿子->爷爷)
void rotate(int x){
int y=e[x].father;
int z=e[y].father;
int yson=identify(x);
int zson=identify(y);
int baby=e[x].ch[yson^1] //原本是“Z”字关系:y->baby,y->x均为yson,但x->baby为yson^1
connect(baby,y,yson);
connect(y,x,yson^1);
connect(x,z,zson);
update(y),update(x); //x,y内部元素个数改变了,更新下
}
//splay瞬移 (即不停地旋转上升 从at->to)
分两种情况://zig-zig , zig-zag

void splay(int at,to){ //起点,终点
to=e[to].father; //以终点父亲作为目标
while(e[at].father!=to){
int up=e[at].father;
if(e[up].father==to)rotate(at);//一步之遥
else if(identify(up)==identify(at))rotate(up),rotate(at); //zig-zig
else rotate(at),rotate(at); //zig-zag
}}
//创建一个绝对新元素节点 (为下面insert服务)
void crepoint(int v,f){ //元素值,父亲 (左右位置根据元素值大小自动匹配)
n++;//总元素序号增加
e[n].v=v;
e[n].father=f;
e[n].sum=e[n].recy=1;
}
//完全摧毁这个元素的节点 (为下面pop服务)
void destroy(int x){
e[x].v=e[x].ch[0]=e[x].ch[1]=e[x].father=e[x].sum=e[x].recy=0;
if(x==n)n--; //小优化,如果是序号是最后一个,那总元素序号就-1
}
public:
//查找v元素值的位置序号 (为下面 pop服务)
int find(int v){
int now=root;
while(1){
if(e[now].v==v){
splay(now,root);//这里必须将now点瞬移到总根处,之后你会知道的
return now;
}
int nxt=e[now].v<v?1:0;
if(!e[now].ch[nxt])return 0;
now=e[now].ch[nxt];
}}
//尝试添加一个v元素值
{
分几种情况:
1.若不存在,crepoint新增一个节点
2.若已存在v元素,那么sum++,recy++
3.从上而下搜索,路途中经过的节点sum值都要+1
}
int insert(int v){
points++;//总元素个数增加
if(n==0){
root=1;
crepoint(v,0);
}else{
int now=root;
while(1){
e[now].sum++;//从上而下搜索,路途中的节点sum值都要+1
if(v==e[now].v){
e[now].recy++;
return now;
}
int nxt=e[now].v<v?1:0;
if(!e[now].ch[nxt]){//找到空缺处,新添节点
crepoint(v,now);
e[now].ch[nxt]=n;//赋上新增的序号
return n;
}
now=e[now].ch[nxt];
}}return 0;}
//与insert函数连锁,每新增一个点,都要把splay瞬移到总根处
void push(int v){
splay(insert(v),root);
}
//尝试删掉一个v元素值
{
分几种情况:
1.不存在v值的点,直接返回
2.存在v值的点,且有好几个,那就删掉一个,sum--,recy--
3.存在v值的点,且只有一个时:
a.destroy直接摧毁这个节点
(deal已经在总根root处)
b.如果没有左儿子,那就将右儿子->总根root
c.如果有左儿子,那就找到左儿子子树中最大的节点splay到左儿子处,再把右儿子->左儿子,左儿子->总根root
}
void pop(int v){
int deal=find(v);//这里的find函数其实已经把deal瞬移到总根了
if(!deal)return;
points--;
if(e[deal].recy>1){
e[deal].recy--; //子树不需要修改了sum,因为deal是总根
e[deal].sum--;
return;
}
if(!e[deal].ch[0]){
root=e[deal].ch[1];
e[root].father=0;
}else{
int lef=e[deal].ch[0];
while(e[lef].ch[1])lef=e[lef].ch[1];//一直往下找左儿子子树中的最深处的最大右儿子
splay(lef,e[deal].ch[0]);
int rig=e[deal].ch[1];
connect(rig,lef,1);
connect(lef,0,1);//默认接总根root都是接在右儿子上
update(lef);
}
destroy(deal);
}
//元素值为v的节点在这棵树里是第几小
{
1.如果往左儿子走,ans不要加左儿子效果
2.如果往右儿子走,ans就要加右儿子的效果(但都要加自身recy)
}
int rk(int v){
int ans=0,now=root;
while(1){
if(v==e[now].v)return ans+e[e[now].ch[0]].sum+1;
if(now==0)return 0;
if(v<e[now].v)
now=e[now].ch[0];
else{
ans+=e[e[now].ch[1]].sum+e[now].recy;
now=e[now].ch[1];
};
return 0;
}
//获取第x小的元素的值(操作与rk正好相反)
int atrk(int x){
if(x>points)return -inf;
int now=root;
while(1){
int dt=e[now].sum-e[e[now].ch[1]].sum; //右边+自己的元素总数
if(x>e[e[now].ch[0]].sum&&x<=dt)break; //如果左边走不得右边也走不得,那就找到这个数了
if(x<dt)now=e[now].ch[0];
else{
x-=dt;
now=e[now].ch[1;
}}
splay(now,root);
return e[now].v;
}
//找刚好大于v的元素值
int upper(int v){
int now=root;
int res=inf;
while(now){
if(e[now].v>v&&e[now].v<res)
res=e[now].v;
if(e[now].v>v)
now=e[now].ch[0];
else
now=e[now].ch[1];
}
return res;
}
//找刚好小于v的元素值
int lower(int v){
int now=root;
int res=-inf;
while(now){
if(e[now].v<v&&e[now].v>res)
res=e[now].v;
if(e[now].v<v)
now=e[now].ch[1];
else
now=e[now].ch[0];
}
return res;
}