模板题:LOJ133
就是区间上的问题搬到了矩阵上。
但其实矩阵上的问题处理起来并不容易。比如这道题,涉及矩阵最大值,必须采用二维线段树(线段树套线段树)的方式进行维护,非常繁琐。
但对于LOJ133这道题,因为只有单点修改区间求和,所以考虑使用二维树状数组,即树状数组套树状数组。而二维树状数组写起来就要简单多了。
比如说,我们要维护一个 \(4\times4\) 的矩阵。我们可以考虑对行建立一个树状数组,再对每一行建立一个树状数组(如下图)。
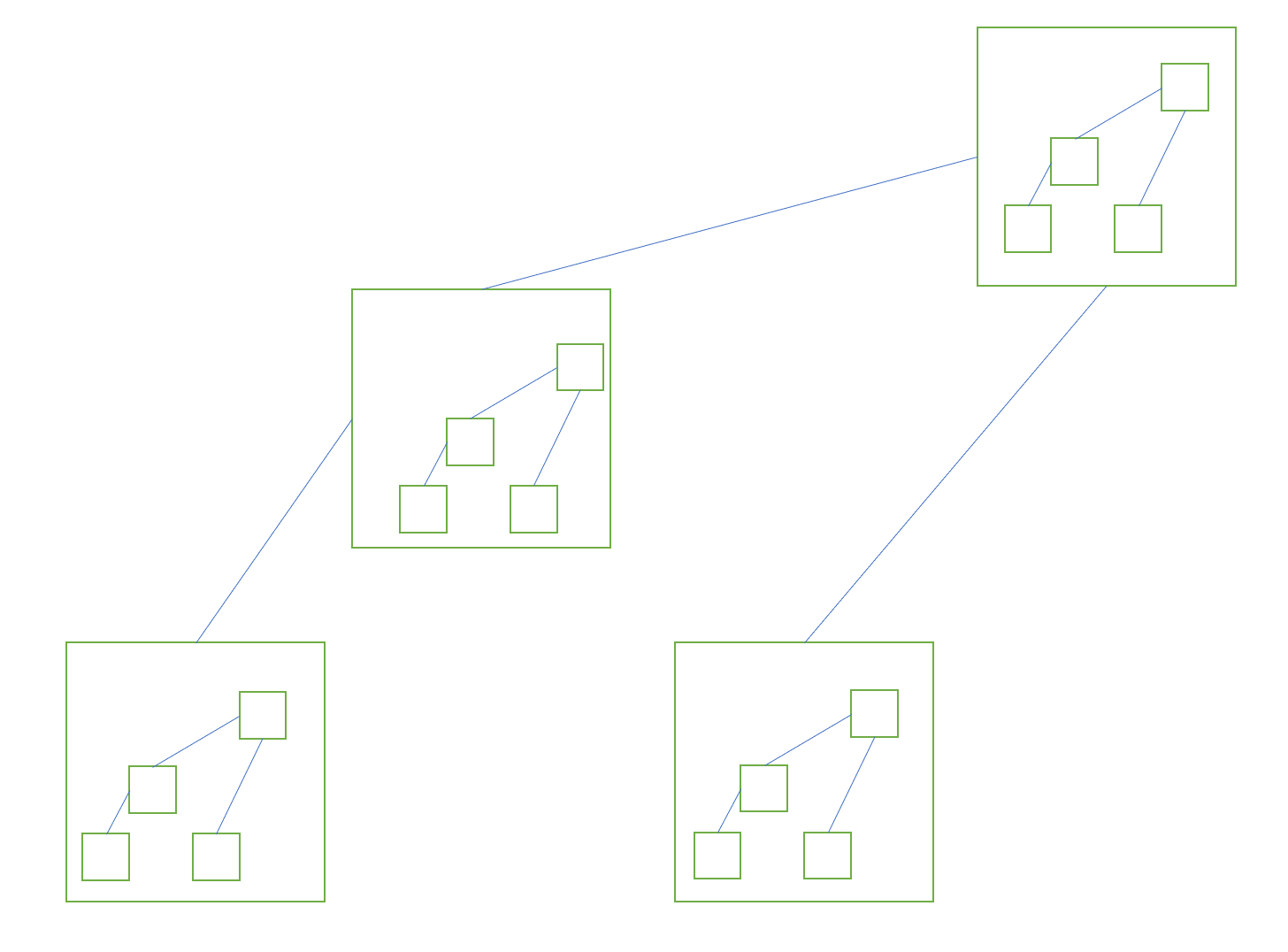
方便起见,我们称外层树状数组(维护行)的结点为外层结点,内层树状数组(维护每一行)的结点为内层结点。
接下来就要支持两个操作了。实在是不好描述,直接放图了。
修改操作:比如我们修改了 \((1,2)\) 这个位置的值,树状数组上要修改的位置如图:

实现:
树状数组没有线段树那样的繁琐结构,直接开二维数组就完事了。
void add(int x,int y,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
a[i][j]+=k;
}
查询同理。显然矩阵查询可以化归为对以 \((1,1)\) 为左上顶点的矩阵的查询。比如我们查询 \((3,3)\):

code:
int query(int x,int y)
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ans+=a[i][j];
return ans;
}
//query(aa,bb;cc,dd)=query(cc,dd)-query(aa-1,dd)-query(cc,bb-1)+query(aa-1,bb-1)
嗯就这么简单。