如果我们只需要找一个模式串在另一个文本串中出现的位置和次数,使用KMP算法即可在线性时间内解决问题。
但是如果模式串的数量不止一个,甚至模式串有包含关系时,我们就需要AC自动机了。
奇怪的知识:AC自动机全称Aho–Corasick算法,是两个人名的组合,就像KMP一样。
1. 朴素AC自动机
AC自动机本质为一个接受且仅接受以某一模式串作为后缀的字符串的DFA。形式上,AC自动机由模式串构成的Trie树和一些fail边组成。
我们定义一个状态的fail边连向这个状态在自动机上的最长真后缀。这样,失配的时候就能通过跳fail边,舍弃当前匹配的前缀来继续匹配。
我们来考虑fail边的具体连法。不妨定义 \(fail(0)=0;\ fail(u)=0,\ \delta(0,u)\neq \text{null}\)。
显然fail边一定连向深度比当前状态小的状态,于是考虑进行bfs,这样我们在连一个状态的fail边时,深度比其小的所有状态都已经有了fail边。
考虑计算 \(fail(\delta(u,c))\)。注意到,\(u\) 状态加上 \(c\) 这个字符的最长真后缀,恰为 \(u\) 状态的最长真后缀再加上 \(c\) 这个字符。
于是我们有以下的计算方法:\(fail(\delta(u,c))=\delta(fail(u),c),\ \delta(fail(u),c)\neq\text{null}\)。
若 \(\delta(fail(u),c)=\text{null}\),则 \(fail(\delta(u,c))=\delta(fail(fail(u)),c),\ \delta(fail(fail(u)),c)\neq\text{null},\cdots\)
直到存在 \(u\) 这条fail链上的点 \(v\) 有 \(\delta(v,c)\neq\text{null}\) 为止。
下面的图是 \(\{\texttt{a},\ \texttt{ba},\ \texttt{bbc},\ \texttt{ca}\}\) 构成的Trie树连接fail边之后的结果。之后的图也都以此为基础。
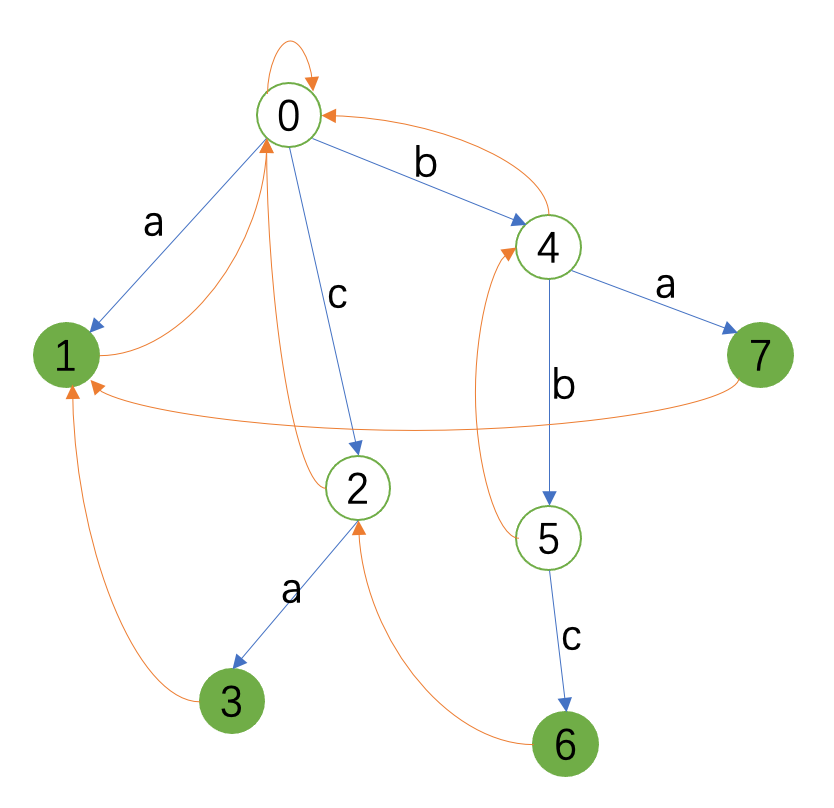
这样的一个结构就已经能够完成多模式串匹配任务了。具体流程如下:
将文本串一个字符一个字符输入进自动机。
如果对于当前状态,Trie树上不存在对应的边,即 \(\delta(u,c)=\text{null}\),那我们就跳fail边,直到存在对应的边为止;
如果到达一个接受状态,那么由该状态向上的fail链中的接受状态也都要计算上。
可以用上面的图手动模拟一下 \(\texttt{ababbca}\) 这个串,应当会得到结果 \(\{\texttt{a}:3,\ \texttt{ba}:1,\ \texttt{bbc}:1,\ \texttt{ca}:1\}\)。
2. 真正的AC自动机
遗憾的是,如果就用上面的方式来构造AC自动机,时间复杂度还是太高了。不论是构造时还是匹配时,暴力跳fail边的操作都会增加AC自动机的时间复杂度。
首先,做匹配统计结果的时候不能每次到达接受状态都暴力跳。
比如说给定模式串 \(\{\texttt{a},\ \texttt{aa},\ \texttt{aaa},\ \texttt{aaaa},\cdots\}\),那么几乎每次统计都要跳满。
正确的操作是这样的:只关心fail边,得到fail树:
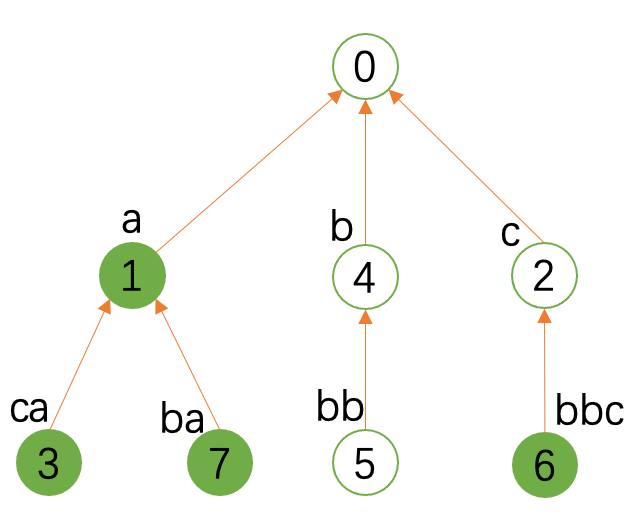
然后每次统计只在对应的状态统计一次,匹配完之后dfs做一个子树和就行了。
这个问题很好解决,但问题在于如何优化构造。还是看计算fail的式子:
\(fail(\delta(u,c))=\delta(fail(u),c),\ \delta(fail(u),c)\neq\text{null}\)。
若 \(\delta(fail(u),c)=\text{null}\),则 \(fail(\delta(u,c))=\delta(fail(fail(u)),c),\ \delta(fail(fail(u)),c)\neq\text{null},\cdots\)
很明显有重复计算的嫌疑。我们的思路是在原Trie树上 \(\delta(u,c)\) 不存在时定义 \(\delta(u,c)=\delta(fail(u),c)\),拓展 \(\delta\) 函数的定义范围。
于是上面的式子变成:\(fail(\delta(u,c))=\delta(fail(u),c)=\delta(fail(fail(u)),c),\cdots\)。
这样我们相当于进行了一个路径压缩,让fail只跳一次,因为 \(\delta(u,c)\) 一定已经按照定义计算出来了。
如果存储所有的 \(\delta\) 值,代码的空间复杂度变为 \(O(n|\Sigma|)\),其中 \(n\) 为状态数,\(\Sigma\) 为字符集大小。
也有动态开空间的写法,需要新值的时候递归计算。
如果我们把所有的 \(\delta(u,c)\) 连同fail边都画出来,结果如下:
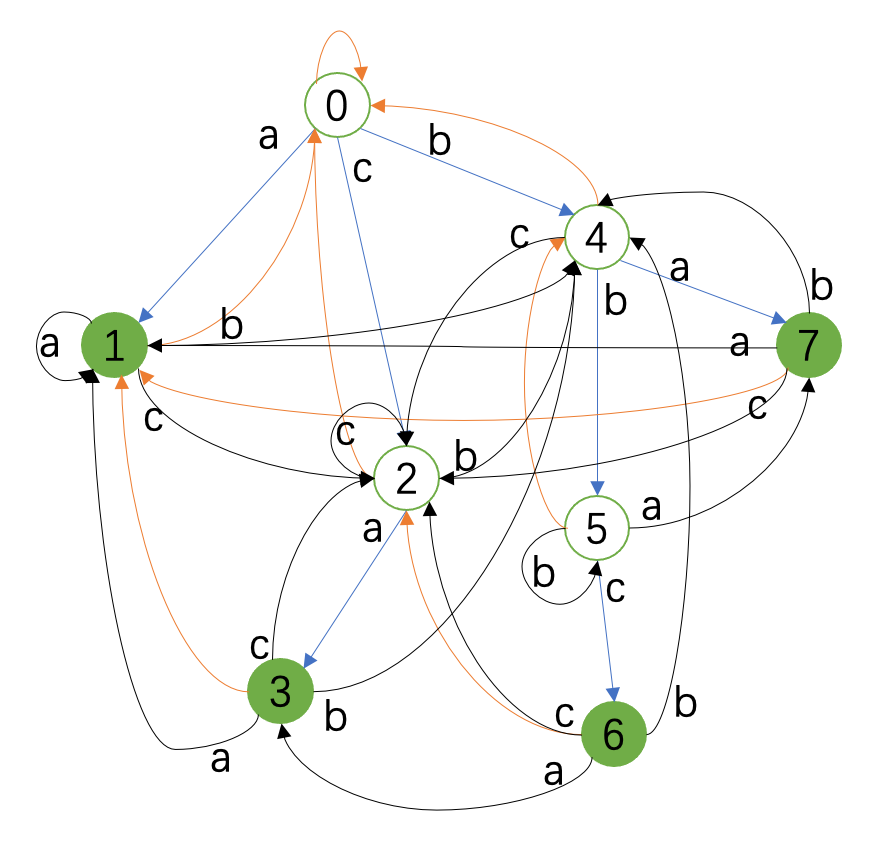
可以看出,新加的黑色的边改变了Trie树的结构。我们称这种结构为Trie图。有了Trie图,我们做匹配的操作也方便了。
根据 \(\delta(u,c)=\delta(fail(u),c)\),我们甚至不用考虑fail边,直接在Trie图上跳就好了,只有最后统计答案的时候会用到fail树。于是我们可以把Trie图和fail树分开来看。
接下来的图就展示了 \(\texttt{ababbca}\) 这个串的匹配情况。
左边是Trie图,右边是fail树;红色代表当前状态,绿色代表接受状态,右边fail树上标记的是当前的统计情况。
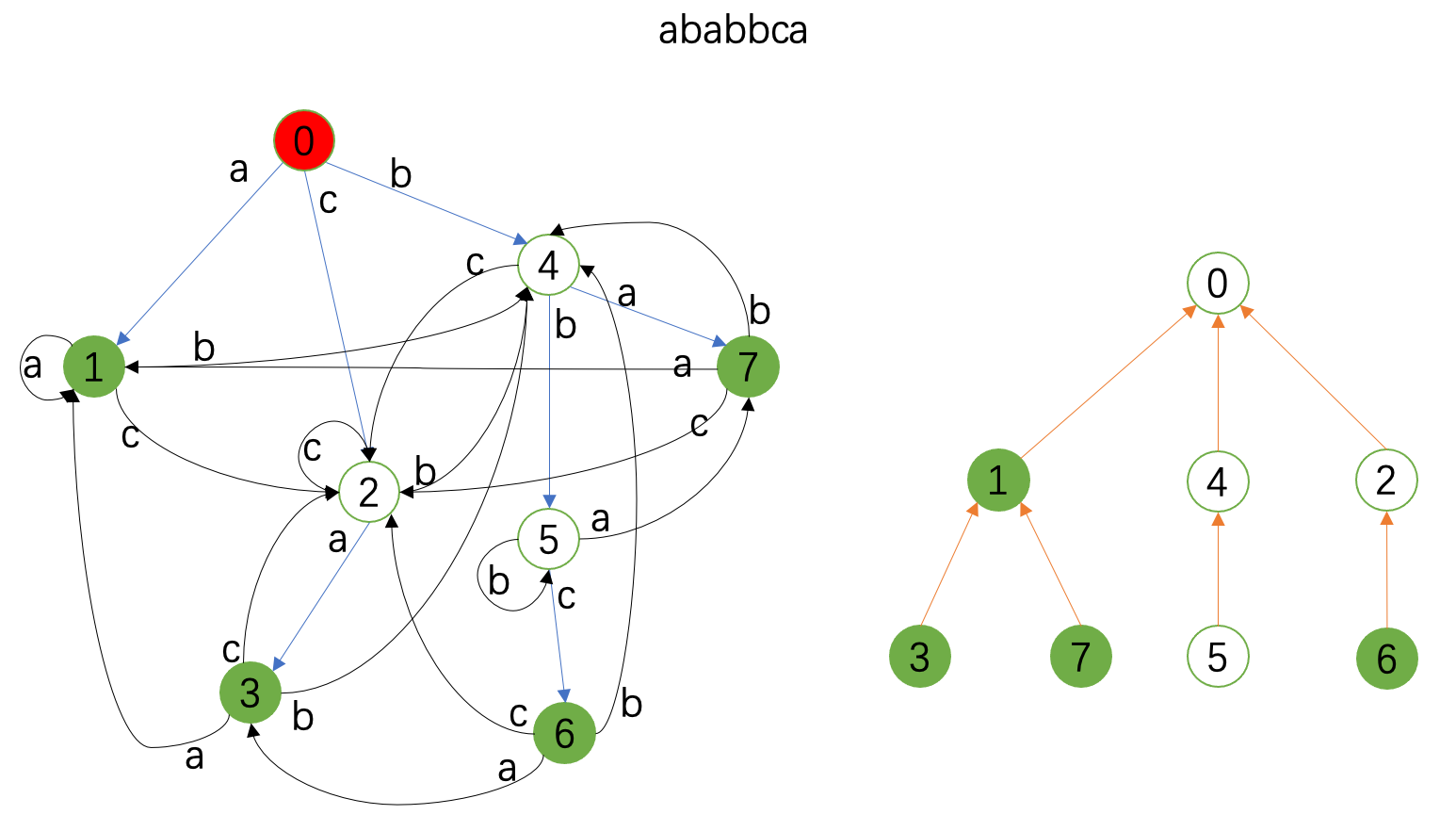
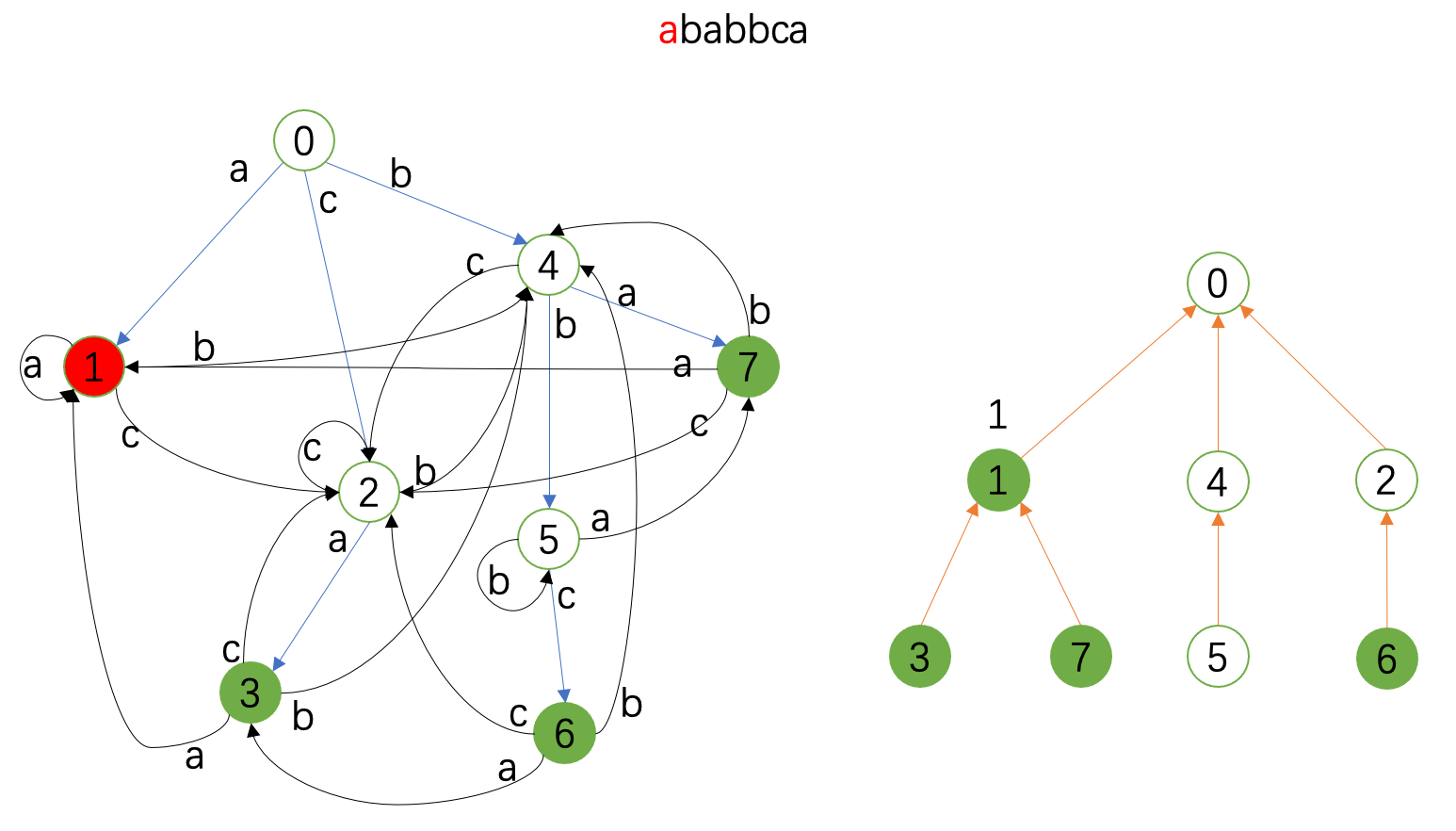
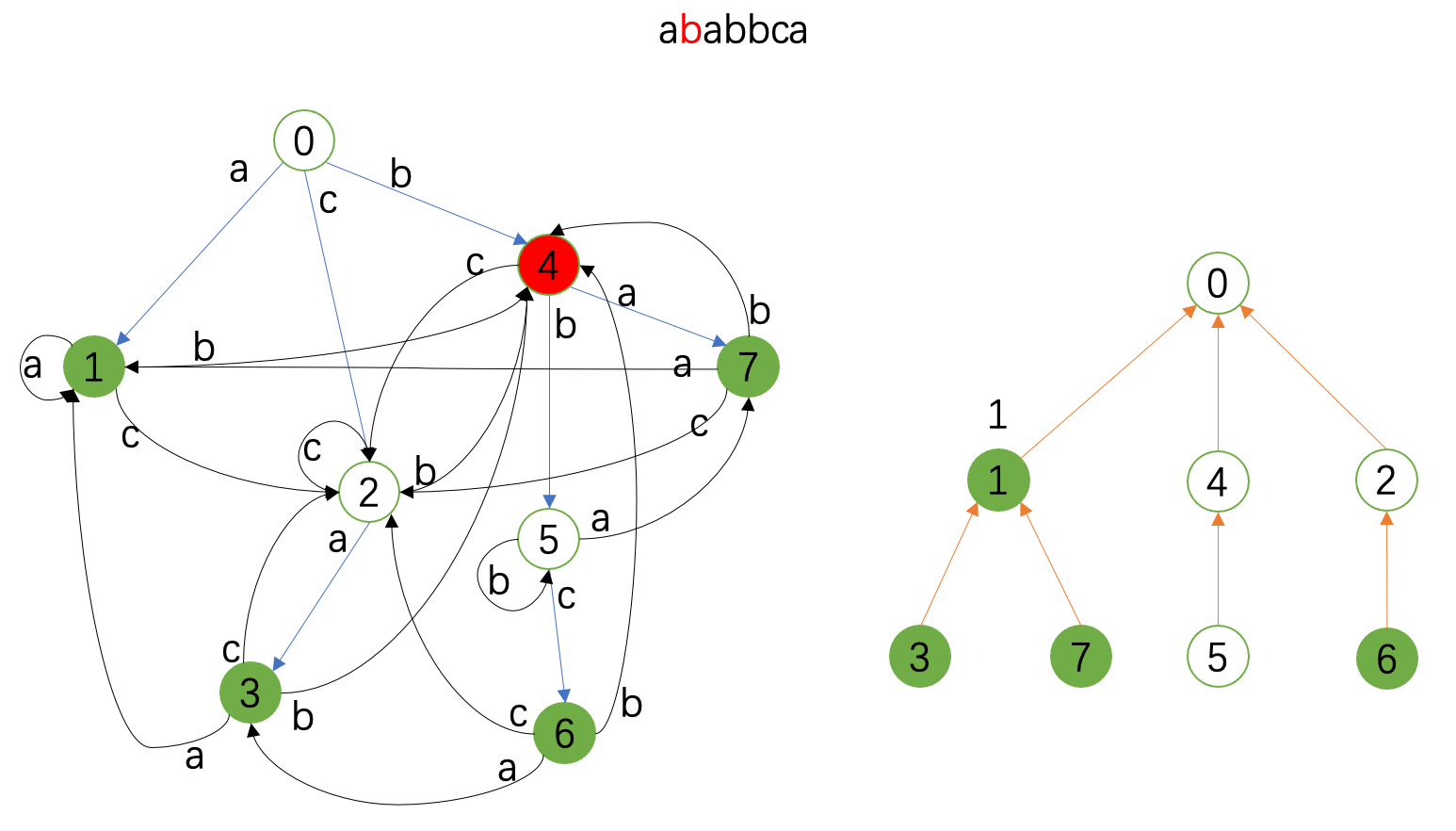
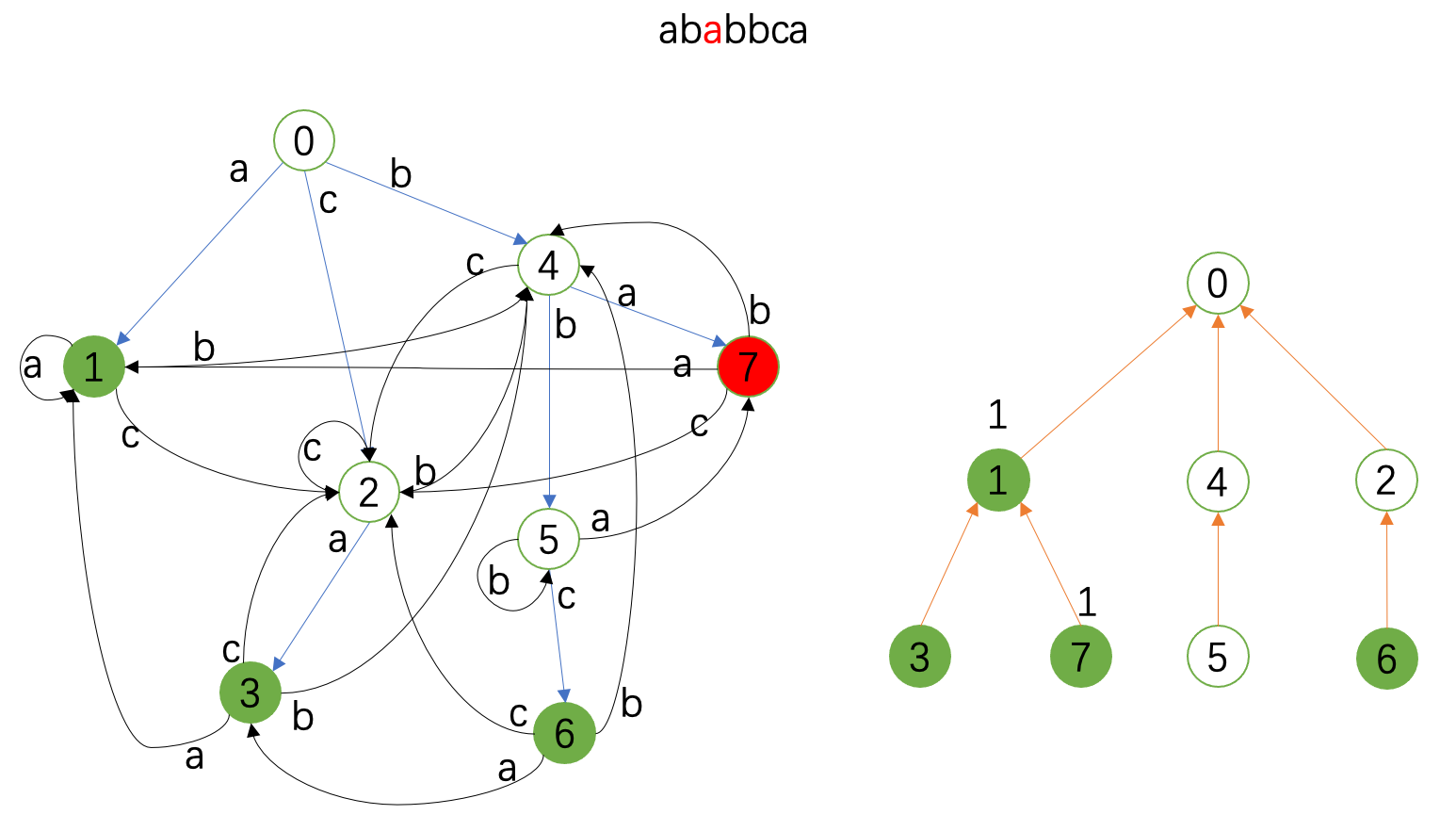
勘误:下面两张图中 \(4\) 和 \(5\) 匹配,在fail树上也要记录,虽然这对例子中的统计没有影响。
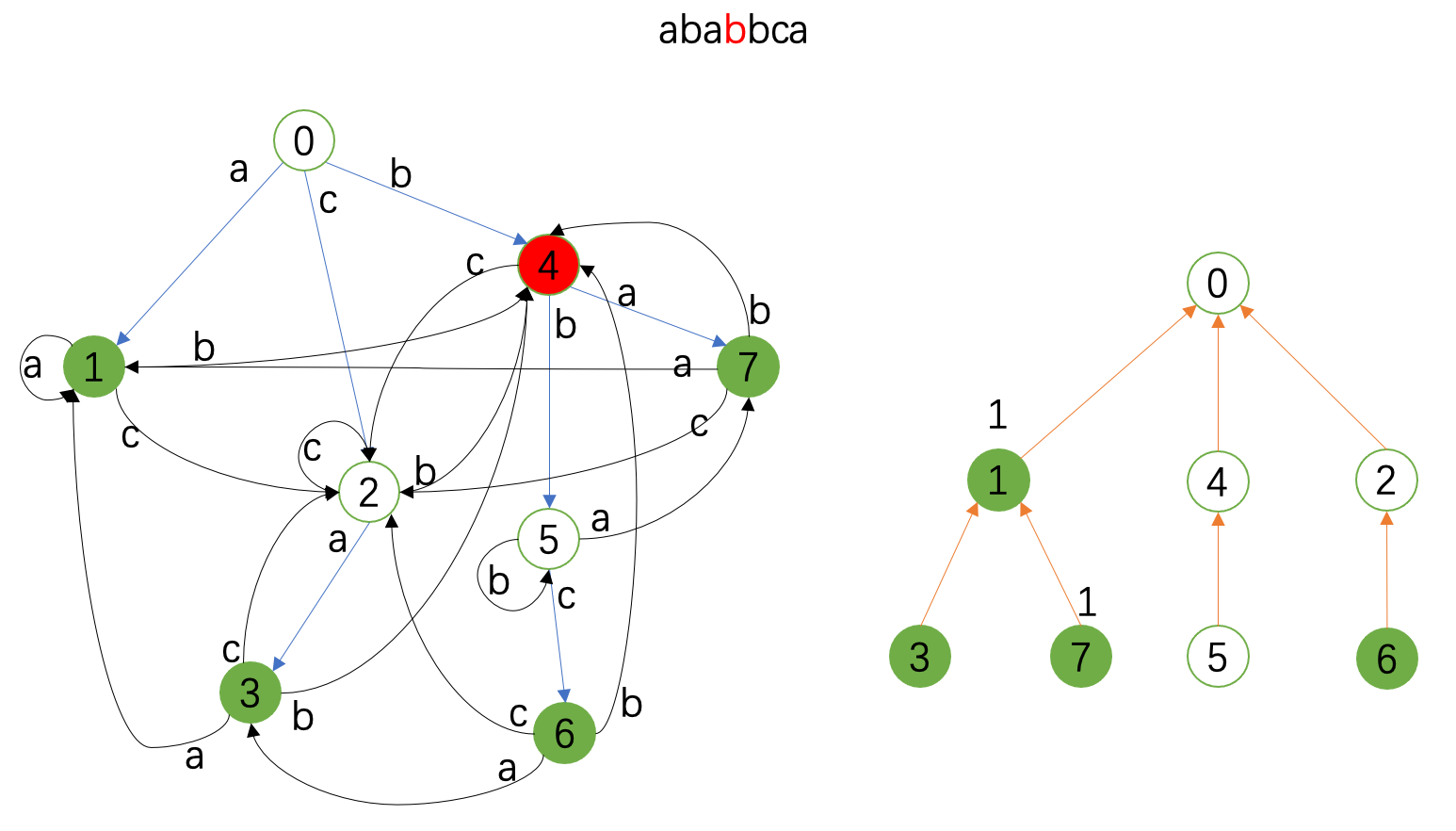
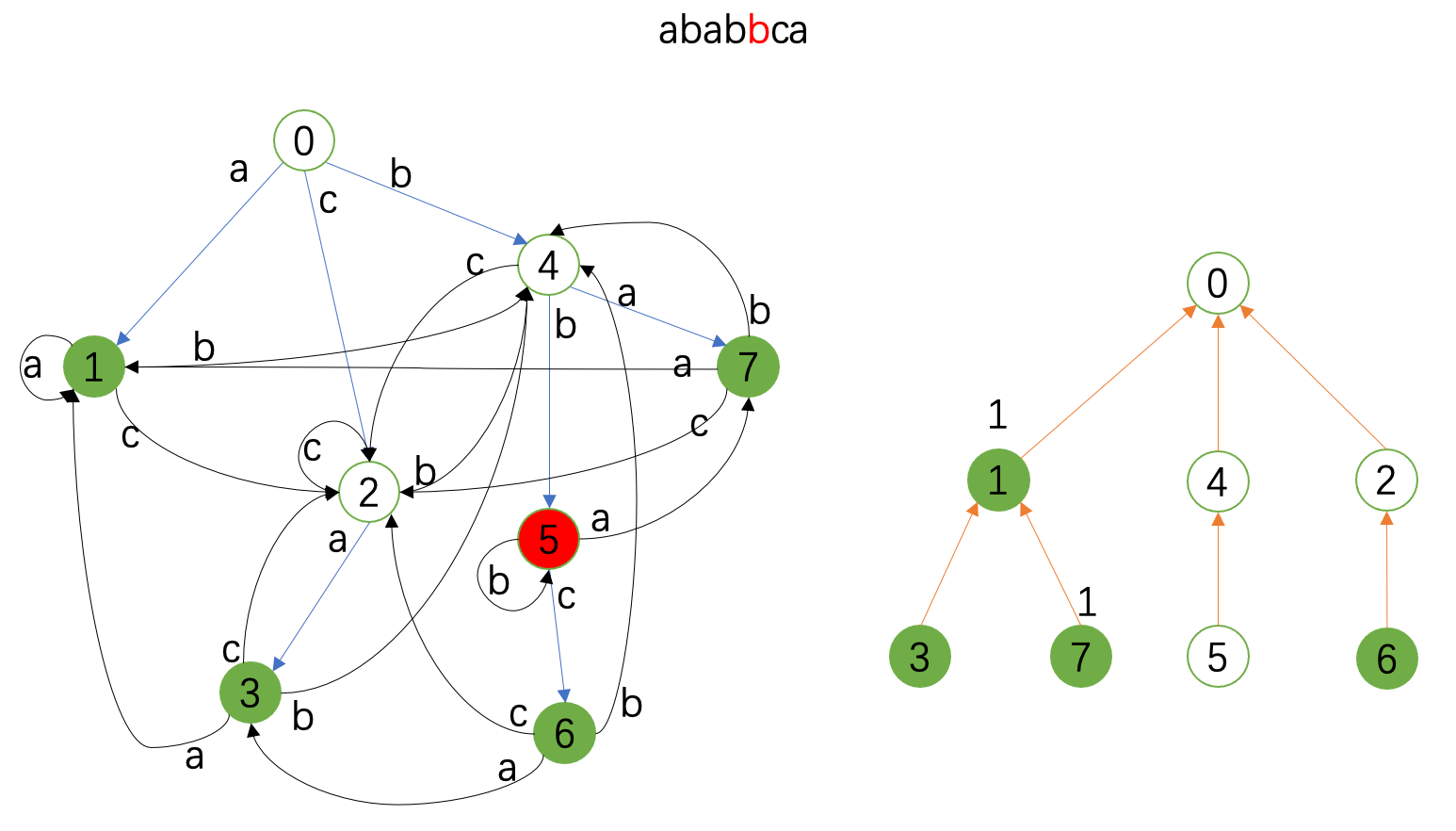
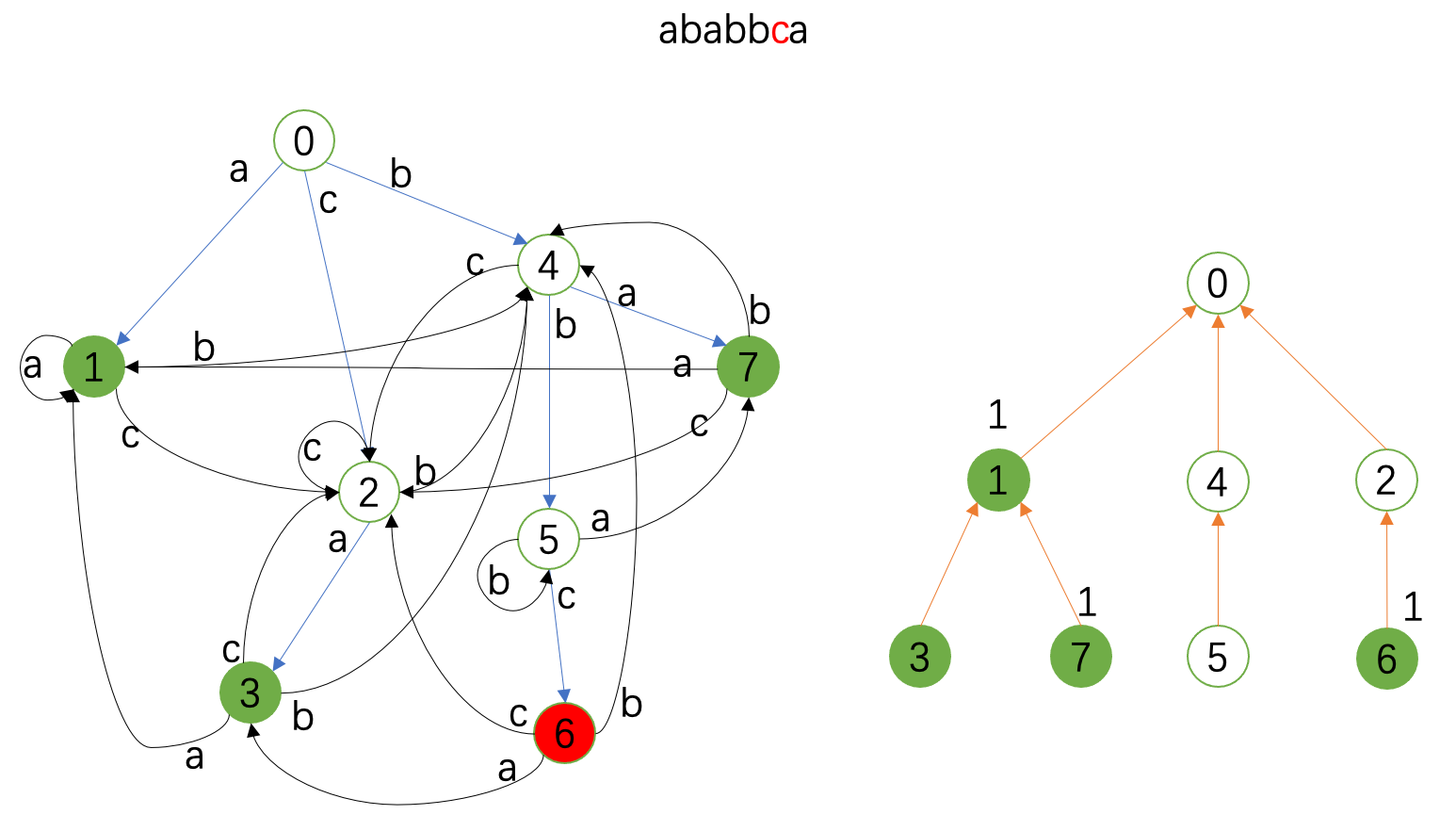
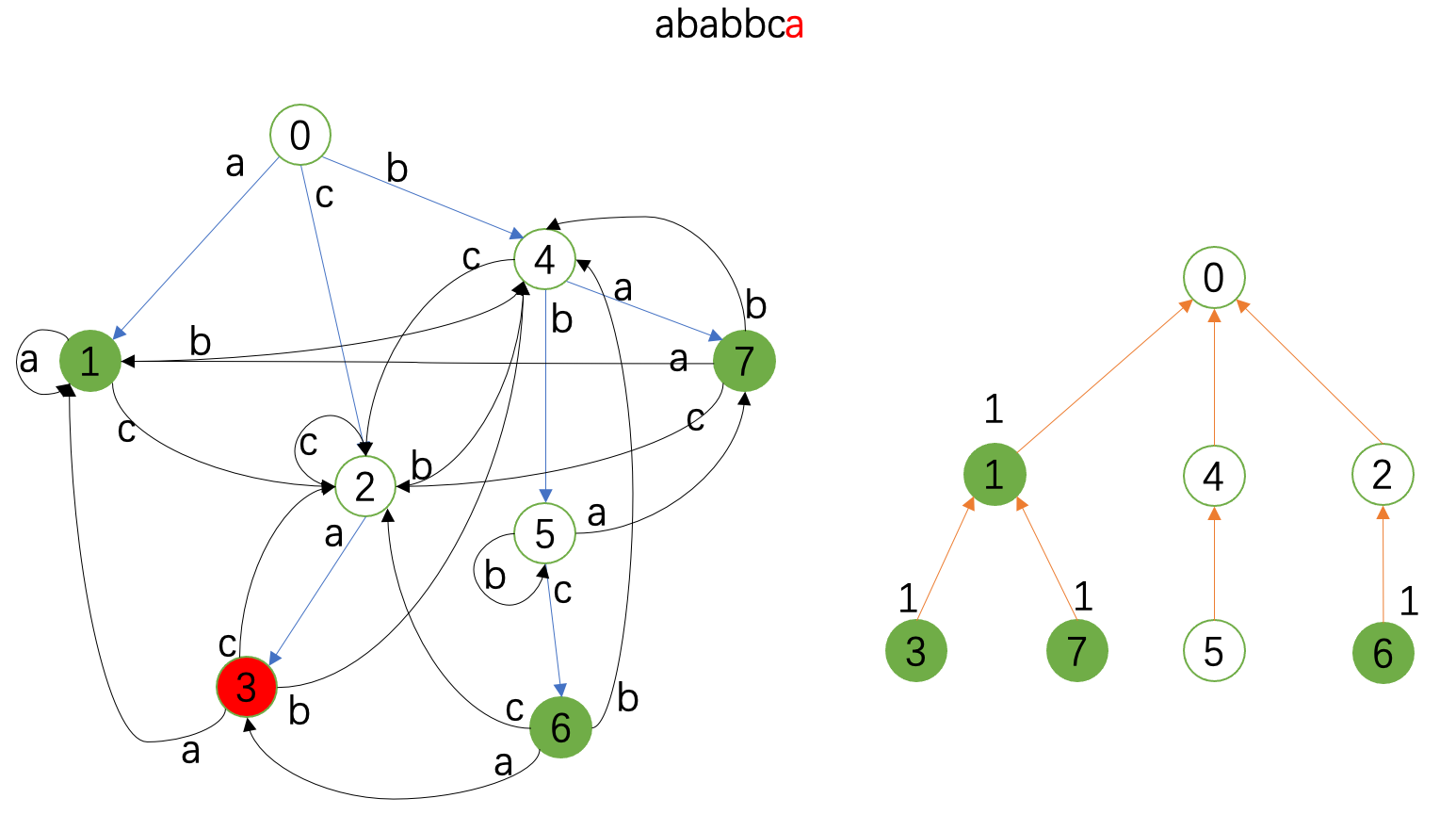
匹配业已完成,最后我们对fail树做子树和得到最终答案。
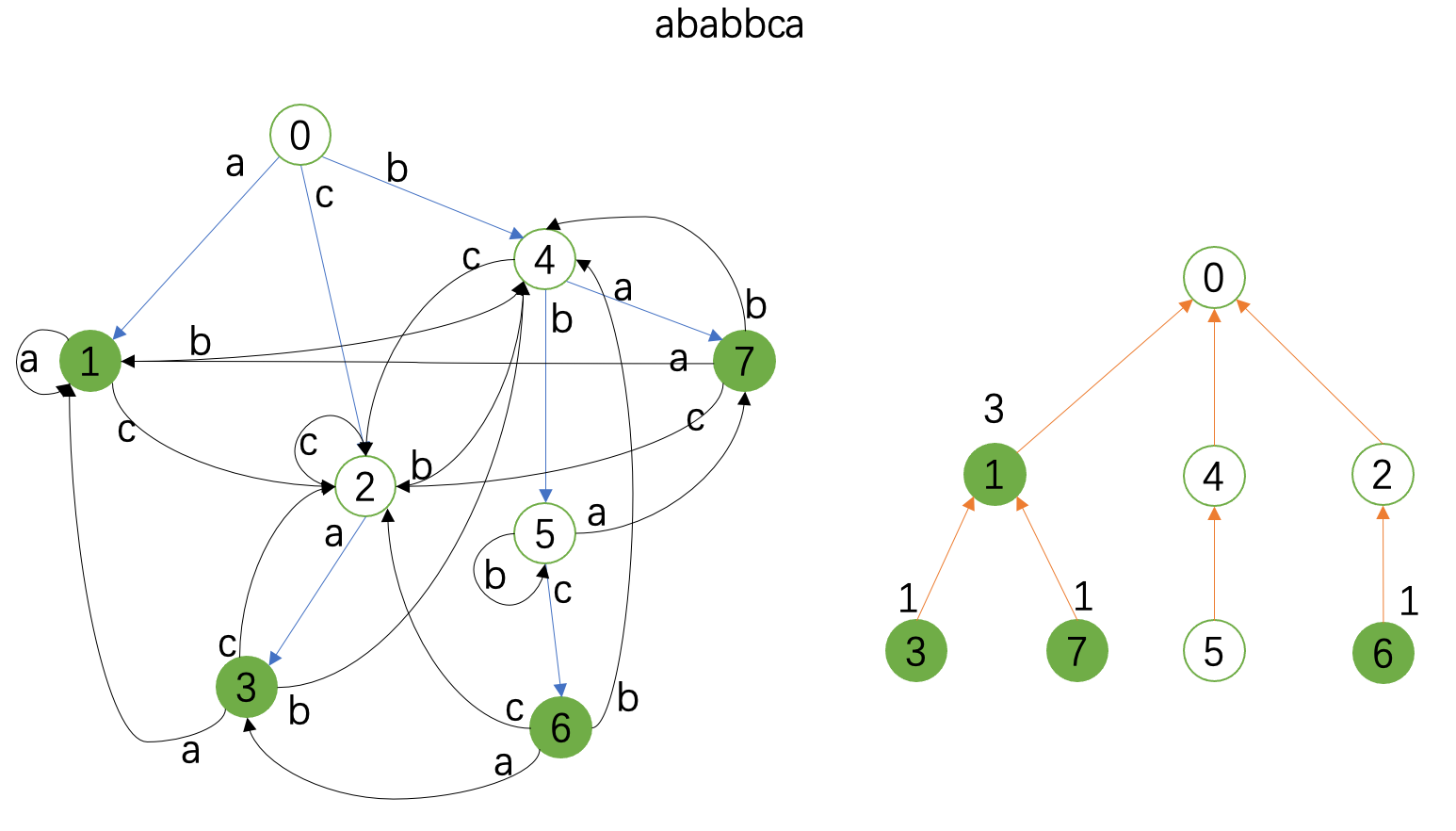
复杂度分析:
时间复杂度:构建 \(O(\Sigma{|s_i|}+n|\Sigma|)\),匹配 \(O(|t|+n)\)
空间复杂度:\(O(n|\Sigma|)\)
最后是代码实现。一步到位,直接做luoguP5357 【模板】AC 自动机(二次加强版):
const int maxn=200010;
int n,tot,trie[maxn][26],fail[maxn],point[maxn];//point[]记录每个模式串在Trie树上对应的节点编号
string s[maxn],t;
queue<int> q;
int cnt,h[maxn],siz[maxn];
struct edge{int to,nxt;}e[maxn];
void addedge(int u,int v)
{
e[++cnt]=(edge){v,h[u]};
h[u]=cnt;
}
void buildtrie()//建立trie树,没什么好说的
{
for(int i=1;i<=n;i++)
{
int u=0,l=s[i].length();
for(int j=0;j<l;j++)
{
int now=s[i][j]-'a';
if(!trie[u][now])trie[u][now]=++tot;
u=trie[u][now];
}
point[i]=u;
}
}
void buildac()
{
for(int i=0;i<26;i++)if(trie[0][i])q.push(trie[0][i]);//我们将根节点的子节点入队,这样可以保证fail指针指的是正确的
while(!q.empty())//bfs
{
int u=q.front();q.pop();
for(int i=0;i<26;i++)
if(trie[u][i])//式子在上面已经写过了
{
fail[trie[u][i]]=trie[fail[u]][i];
q.push(trie[u][i]);
}
else trie[u][i]=trie[fail[u]][i];
}
}
void match(string ss)//匹配时一个一个字符跳就行
{
int u=0,l=ss.length();
for(int i=0;i<l;i++)
{
u=trie[u][ss[i]-'a'];
siz[u]++;
}
}
void dfs(int u)//dfs统计子树和
{
for(int i=h[u];i;i=e[i].nxt)
{
int p=e[i].to;
dfs(p);
siz[u]+=siz[p];
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin >> n;
for(int i=1;i<=n;i++)cin >> s[i];
buildtrie();buildac();
cin >> t;match(t);
for(int i=1;i<=tot;i++)addedge(fail[i],i);//建立fail树
dfs(0);
for(int i=1;i<=n;i++)cout << siz[point[i]] << endl;
return 0;
}