万欧 / 类欧
类欧几里得算法
板板。
【模板】类欧几里得算法
#include<bits/stdc++.h>
#define ll long long
#define N 22
#define P 998244353
ll t,p,q,r,l;
struct Po{
ll cntu,cntr,sumi,sums,sqrs,prod;
Po(){cntu = cntr = sumi = sums = sqrs = prod = 0;}
Po operator + (Po b) {
Po c;
c.cntu=(cntu+b.cntu)%P,c.cntr=(cntr+b.cntr)%P;
c.sumi=(sumi+b.sumi+cntr*b.cntr)%P;
c.sums=(sums+b.sums+cntu*b.cntr)%P;
c.sqrs=(sqrs+b.sqrs+((cntu*cntu)%P)*b.cntr+(2*cntu*b.sums)%P)%P;
c.prod=((prod+b.prod+((cntu*cntr)%P)*b.cntr)%P+cntu*b.sumi+cntr*b.sums)%P;
return c;
}
}nu,nr,ans;
inline Po pow(Po a,ll k){
Po res;
while(k){
if(k & 1){res = res + a;}
a = a + a;
k >>= 1;
}
return res;
}
inline ll div(ll a,ll b,ll c,ll d){return ((long double)1.0 * a * b + c) / d;}
inline Po solve(ll p,ll q,ll r,ll l,Po a,Po b){
if(!l)return Po();
if(p >= q)return solve(p % q,q,r,l,a,pow(a,p / q) + b);
ll m = div(l,p,r,q);
if(!m)return pow(b,l);
ll cnt = l - div(q,m,-r - 1,p);
return pow(b,(q - r - 1) / p) + a + solve(q,p,(q - r - 1) % p,m - 1,b,a) + pow(b,cnt);
}
int main(){
scanf("%lld",&t);
while(t -- ){
scanf("%lld%lld%lld%lld",&l,&p,&r,&q);
nu.cntu = 1,nu.cntr = nu.sumi = nu.sums = nu.sqrs = nu.prod = 0;
nr.cntu = nr.sums = nr.sqrs = nr.prod = 0,nr.sumi = nr.cntr = 1;
ans = pow(nu,r / q) + solve(p,q,r % q,l,nu,nr);
printf("%lld %lld %lld\n",(ans.sums+r/q)%P,(ans.sqrs+((r/q)%P)*((r/q)%P))%P,ans.prod);
}
}
万能欧几里得
把其看做\(\sum a^xb^y\)类型。
则可写作矩阵:
\(\begin{bmatrix}\sum_x a^xb^y\\a^xb^y\end{bmatrix}\)\(\begin{bmatrix}1&0\\0&b\end{bmatrix}\)\(\begin{bmatrix}1&a\\0&1\end{bmatrix}\)
那么把\(a,b\)写作矩阵形式也可以
素数 及 取膜问题
【模板】Pollard-Rho 算法
先判断一个数是否是质数,使用Miller Rabin测试,否则用Pollard Rho算法 找到一个因数,递归操作\(n / p\)和\(p\)。
【模板】Pollard-Rho 算法
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int t;
long long max_factor, n;
long long gcd(long long a, long long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
long long quick_pow(long long x, long long p, long long mod) { //快速幂
long long ans = 1;
while (p) {
if (p & 1) ans = (__int128)ans * x % mod;
x = (__int128)x * x % mod;
p >>= 1;
}
return ans;
}
bool Miller_Rabin(long long p) { //判断素数
if (p < 2) return 0;
if (p == 2) return 1;
if (p == 3) return 1;
long long d = p - 1, r = 0;
while (!(d & 1)) ++r, d >>= 1; //将d处理为奇数
for (long long k = 0; k < 10; ++k) {
long long a = rand() % (p - 2) + 2;
long long x = quick_pow(a, d, p);
if (x == 1 || x == p - 1) continue;
for (int i = 0; i < r - 1; ++i) {
x = (__int128)x * x % p;
if (x == p - 1) break;
}
if (x != p - 1) return 0;
}
return 1;
}
long long Pollard_Rho(long long x) {
long long s = 0, t = 0;
long long c = (long long)rand() % (x - 1) + 1;
int step = 0, goal = 1;
long long val = 1;
for (goal = 1;; goal *= 2, s = t, val = 1) { //倍增优化
for (step = 1; step <= goal; ++step) {
t = ((__int128)t * t + c) % x;
val = (__int128)val * abs(t - s) % x;
if ((step % 127) == 0) {
long long d = gcd(val, x);
if (d > 1) return d;
}
}
long long d = gcd(val, x);
if (d > 1) return d;
}
}
void fac(long long x) {
if (x <= max_factor || x < 2) return;
if (Miller_Rabin(x)) { //如果x为质数
max_factor = max(max_factor, x); //更新答案
return;
}
long long p = x;
while (p >= x) p = Pollard_Rho(x); //使用该算法
while ((x % p) == 0) x /= p;
fac(x), fac(p); //继续向下分解x和p
}
int main() {
scanf("%d", &t);
while (t--) {
srand((unsigned)time(NULL));
max_factor = 0;
scanf("%lld", &n);
fac(n);
if (max_factor == n) //最大的质因数即自己
printf("Prime\n");
else
printf("%lld\n", max_factor);
}
return 0;
}
CF1334E Divisor Paths
猜结论。
如果\(a,b\)有倍数关系,那就是一直变大。
否则先走到\(gcd(a,b)\)。
[CQOI2018]破解D-H协议
\(BSGS\)板板题。
[CQOI2018]破解D-H协议
#include<bits/stdc++.h>
#define ll long long
ll g,p;
int t;
ll a,b;
std::map<ll,int>Q;
inline ll Pow(ll ai,ll bi){
ll ans = 1;
while(bi){
if(bi & 1)ans = ans * ai % p;
ai = ai * ai % p;
bi >>= 1;
}
return ans;
}
inline void del(){
Q.clear();
ll s = std::sqrt(p) + 1;
ll B = 1;
// puts("Part B");
for(int i = 0;i <= s;++i){
// std::cout<<i<<" "<<a*B%p<<std::endl;
Q[a * B % p] = i;
B = B * g % p;
}
ll res = 0;
// puts("Part A");
for(int i = 0;i <= s;++i){
ll k = Pow(g,i * s);
if(Q.find(k) != Q.end()){
res = i * s - Q[k];
if(res > 0)
break;
}
}
std::cout<<Pow(b,res)<<std::endl;
return ;
}
int main(){
scanf("%lld%lld",&g,&p);
scanf("%d",&t);
while(t -- ){
scanf("%lld%lld",&a,&b);
del();
}
}
min-max容斥。
[HAOI2015]按位或
考虑对每位依次考虑。
设\(a_k\)为第\(k\)个二进制位为\(1\)的时间。
求\(E(\max(U))\)(\(U\)为全集)。
考虑如何求出\(E(\min(U))\)。
有\(\sum v * P(v)\)
设\(P(S)\)为选中集合\(S\)的概率,\(P'(S)\)为选中集合\(S\)的自己的概率。
那么\(\min(S) = k\)的概率就是:前\(k - 1\)次选了\(S\)的补集的子集,最后一次不能选\(S\)的补集的子集。
那么其\(\min(S)\)的概率为\(P(k) = P'(S \bigoplus U)^{k - 1}(1 - P'(S \bigoplus U))\)
设\(P'(S \bigoplus U)) = p\)
那么\(E(\min(S)) = \sum_{k = 1}^{\infty} k * P(k) = (1 - p) \sum_{k = 1}^{\infty}k * p^{k - 1}\)
错位相减有\((1 - p)Sum = \frac{1}{1 - p}\)
所以有\(E(\min(S)) = \frac{1}{1 - P'(S \bigoplus U)}\)
我们要求出\(P'(所有集合)\)。
使用DWT即可。
不过我不会(焯!)。
借cmd代码一用。
[HAOI2015]按位或
#include<algorithm>
#include<cstdio>
#define Maxn 1100000
using namespace std;
int n;
double a[Maxn];
int siz[Maxn];
int main()
{
scanf("%d",&n);n=(1<<n);
for (int i=0;i<n;i++)scanf("%lf",&a[i]);
for (int len=1;len<n;len<<=1)
for (int p=0;p<n;p+=len+len)
for (int i=p;i<p+len;i++)
a[i+len]+=a[i];
double ans=0;
for (int i=1;i<n;i++){
siz[i]=siz[i>>1]+(i&1);
double sav=(1-a[i^(n-1)]);
if (sav<1e-8){puts("INF");return 0;}
sav=1/sav;
ans+=(siz[i]&1) ? -sav:sav;
}printf("%.10lf",-ans);
return 0;
}
重返现世
考虑直接扩展\(Min - Max\)容斥一下。
则有\(ans = \sum_{T \in S}(-1) ^ {|T| - k} \binom{|T| - 1}{k - 1} E(min(T))\)
发现其\(O(2^n)\)无法直接统计。
发现其\(m \leq 100000\),思考一个和\(m\) 有关的\(dp\)。
考虑依次加入,\(|T|\),\(E(min(T))\),其中\(E(min(T))\)和\(\sum_{i\in T}p_i\)直接相关。
那就直接设计到状态里\(f[i][j][k]\)表示前\(i\)个,选了\(j\)个,\(\sum_{j\in T}p_i = k\)的方案数。
那么直接转移。
此时\(O(n^2m)\),可以获得 \(70\) 分的好成绩。
70分代码
#include<bits/stdc++.h>
#define ll long long
#define N 1005
#define M 10005
#define mod 998244353
int n,ki,m;
ll f[2][N][M];
int p[N];
ll s[N],inv[N];
inline ll Pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1)
ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans % mod;
}
inline ll C(int a,int b){
// std::cout<<a<<" "<<b<<" "<<s[a] * inv[b] % mod * inv[a - b] % mod<<std::endl;
if(a < b)return 0;
return s[a] * inv[b] % mod * inv[a - b] % mod;
}
ll ans = 0;
int main(){
std::memset(f,sizeof(f),0);
scanf("%d%d%d",&n,&ki,&m);
ki = n - ki + 1;
s[0] = 1;
for(int i = 1;i <= n;++i)
s[i] = i * s[i - 1] % mod;
inv[n] = Pow(s[n],mod - 2);
for(int i = n - 1;i >= 0;--i)
inv[i] = (inv[i + 1] * (i + 1)) % mod;
for(int i = 1;i <= n;++i)
scanf("%d",&p[i]);
f[1][0][0] = 1;
for(int i = 1;i <= n;++i){
int now = i & 1;
for(int j = 0;j <= n;++j)
for(int k = 0;k <= m;++k){
// std::cout<<i<<" "<<j<<" "<<k<<" "<<f[now][j][k]<<std::endl;
if(f[now][j][k]){
// puts("TO");
int to = (i + 1) & 1;
f[to][j][k] += f[now][j][k];
f[to][j][k] %= mod;
// std::cout<<"to"<<i + 1<<" "<<j<<" "<<k<<" "<<f[to][j][k]<<std::endl;
f[to][j + 1][k + p[i]] += f[now][j][k];
f[to][j + 1][k + p[i]] %= mod;
// std::cout<<"to"<<i + 1<<" "<<j + 1<<" "<<k + p[i]<<" "<<f[to][j + 1][k + p[i]]<<std::endl;
}
}
for(int j = 0;j <= n;++j)
for(int k = 0;k <= m;++k)
f[now][j][k] = 0;
}
for(int j = 1;j <= n;++j)
for(int k = 0;k <= m;++k)
if(f[(n + 1) & 1][j][k]){
// std::cout<<j <<" "<<k<<" "<<f[(n + 1) & 1][j][k]<<" "<<C(j - 1,ki - 1)<<" "<<Pow(k,mod - 2)<<" "<<Pow(k,mod - 2) * k % mod<<std::endl;
ans = (ans + (((((j - ki)) % 2 ? (-1 * C(j - 1,ki - 1) + mod): (C(j - 1,ki - 1))) * f[(n + 1) & 1][j][k] % mod) * Pow(k,mod - 2) % mod)) % mod;
}
std::cout<<ans * m % mod<<std::endl;
}
考虑这个dp已经没啥优化的前途了。
我们把他降维打击,把整个柿子的一部分丢入方程中。
考虑\(k <= 11\),新维度应是\(k\)。
设\(f_{i,j}\)表示前\(i\)个物品\(\sum_{i \in T}p_i = j\)的\((-1) ^ {|T| - k} \binom{|T| - 1}{k - 1}\)的和。
考虑若不选的话\(f[i][j] += f[i - 1][j]\)
若选的话就要思考有点不对了\(f[i][j + p[i]] = f[i - 1][j] + \delta\),那么我们要思考\(\delta\)是啥。
拆开组合数。
\((-1)^{|T| - k + 1} \binom{|T|}{k - 1} = (-1) ^ {|T| - k + 1}[\binom{|T|}{k - 2} + \binom{|T| - 1}{k - 1}]\).
知\(sum (-1) ^ {|T| - k + 1}\binom{|T|}{k - 2} - \sum (-1) ^{|T| - k}\binom{|T| - 1}{k - 1}\)
我们发现我们只要多记录一维 \(k\) 即可。
\(f[i][j][k]\),\(\sum_{i\in T}p_i = j\)的权值\(\sum (-1)^{|T| - k}\binom{|T| - 1}{k - 1}\)
如果强制选其的话\(f_{i,j + p[i],k} = f_{i - 1,j,k - 1} + f_{i - 1,j,k}\)
\(f[0][0][0] = 1\)。
100分
#include<algorithm>
#include<cstdio>
#include<map>
#define mod 998244353
#define MaxM 10050
#define mod 998244353
using namespace std;
long long f[MaxM][15],ans;
int n,kk,m,p[MaxM];
long long powM(long long a,long long t)
{
long long ans=1;
while(t){
if (t&1)ans=ans*a%mod;
a=a*a%mod;
t>>=1;
}return ans;
}
int main()
{
scanf("%d%d%d",&n,&kk,&m);kk=n-kk+1;
for (int i=1;i<=n;i++)scanf("%d",&p[i]);
f[0][0]=1;
for (int i=1;i<=n;i++)
if (p[i])
for (int j=m-p[i];j>=0;j--)
for (int k=kk;k;k--)
f[j+p[i]][k]=(f[j+p[i]][k]+f[j][k-1]-f[j][k])%998244353;
for (int j=1;j<=m;j++)
ans=(ans+f[j][kk]*m%mod*powM(j,mod-2))%mod;
printf("%lld",(ans+mod)%mod);
return 0;
}
FWT/FMT
【模板】快速莫比乌斯/沃尔什变换 (FMT/FWT)
板板题。
【模板】快速莫比乌斯/沃尔什变换 (FMT/FWT)
#include<bits/stdc++.h>
#define ll long long
#define N (1 << 18)
#define mod 998244353
#define inv2 499122177
int n;
ll a[N],b[N],A[N],B[N];
inline void FWT_or(ll *f,int type){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i)
f[i + mid] = (f[i + mid] + f[i] * type + mod) % mod;
}
inline void FWT_and(ll *f,int type){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i)
f[i] = (f[i] + f[i + mid] * type + mod) % mod;
}
inline void FWT_xor(ll *f,int type){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i)
{
ll x = f[i],y = f[i + mid];
f[i] = (x + y) % mod * (type == 1 ? 1 : inv2) % mod;
f[i + mid] = (x - y + mod) % mod * (type == 1 ? 1 : inv2) % mod;
}
}
inline void work(void (*FWT)(ll *f,int type)){
for(int i = 0;i < n;++i)a[i] = A[i],b[i] = B[i];
FWT(a,1),FWT(b,1);
for(int i = 0;i < n;++i)a[i] = a[i] * b[i] % mod;
FWT(a,-1);
for(int i = 0;i < n;++i)
std::cout<<a[i]<<" ";
puts("");
}
int main(){
scanf("%d",&n);
n = 1 << n;
for(int i = 0;i < n;++i)
scanf("%d",&A[i]),A[i] %= mod;
for(int i = 0;i < n;++i)
scanf("%d",&B[i]),B[i] %= mod;
work(FWT_or);work(FWT_and);work(FWT_xor);
}
行列式
[省选联考 2020 A 卷] 作业题
求无向图的所有生成树的权值和。
一颗生成树的权值定义为:
\(val(T) = (\sum_{i = 1}^{n - 1}w_{e_i}) \times \gcd(w_{e1},w_{e2},......w_{e_{n - 1}}\ )\)
考虑我们直接先反演去掉后面的条件。
那么等价于我们每次枚举因子,把符合条件的边加入矩阵然后。
那么我们只需要求如何得到\((\sum_{i = 1}^{n - 1}w_{e_i})\)。
考虑如果是边权相乘,那我将绝杀,可惜乘不得。
考虑我们改边权为\(wx+1\)的二阶多项式,并在膜\(x^2\)下操作。
消元时我们直接求逆即可。
二阶膜\(x^2\)的\((a+bx)\)的逆为\((a^{-1} - ba^{-2}x)\)
[NOI2021] 路径交点
给定有\(LGV\)引理:
有向无环图\(G\)中,有点\(a_1,...a_n\),和\(b_1,...b_n\),这\(2 \times n\)分别属于\(n\)条不交路径,设其权值为\(-1^{\zeta(p)}\),\(\zeta(p)\)为\(a\to b\)匹配的逆序对数量,则\(M\)的行列式为\(a \to b\)的所有不交路径对应匹配的权值和,\(M_{i,j}\)为\(a_i \to b_j\)的方案数,然后发现偶数减计数正和其行列式定义相等。
我们发现这\(n\)层图的交点个数的奇偶性正和其首尾匹配的逆序对奇偶性相等。
把给定的\(k\)个矩阵全乘起来得到\(M\),然后行列式板子一下就好了。
复杂度为\(O(2kn^3)\)。
期望与概率
[ZJOI2020] 传统艺能
考虑拆贡献为每个点上。
考虑每多操作一次询问我们思考其之和前面\(k - 1\)次的最终期望有关。
我们每个点维护三个状态,祖先和自己的都没有标记,自己有标记,祖先有标记。
如果祖先有标记,那么在访问到兄弟节点时自己会得到标记。
如果自己有标记,访问到子树内节点会失去。
如果在覆盖的情况下访问到该节点,无论如何都会得到标记。
考虑有五种情况:
访问到了自己,访问到祖先,访问到儿子,访问到兄弟,询问不交。
[MtOI2019]小铃的烦恼
诈骗题,很难不下雨。
不过还是蛮好的题。
考虑每次都会成功。
我们枚举最后成为答案的元素。
发现一个元素成为最终元素的概率,取决于一开始的最终元素的概率。
设\(p_i\)为此时有\(i\)个目标元素,使全部元素都变成目标元素的概率。
那么有\(p_i = \frac{i(n - i)}{n(n - 1)}(p_{i - 1} + p_{i + 1}) + (1 - 2\frac{i(n - i)}{n(n - 1)})p_i\)
容易看出\(2p_i = p_{i - 1} + p_{i + 1}\)
所以其为等差数列。
知\(p_0 = 0,p_n = 1\),所以有\(p_i = \frac{i}{n}\)
接下来考虑期望问题,考虑\(f_i\)表示为最终元素的数量为\(n\)时的期望步数,先给出方程:\(f_i = \frac{n(n - 1)}{2i({n - i})} + \frac{i - 1}{2i}f_{i - 1} + \frac{i + 1}{2i}f_{i + 1}\).
考虑我们求出的概率等同于什么呢。
等同于其在所有成功状态中的数量。
我们有从\(f_i\)往其他状态转移的期望的步数为\(\frac{n(n - 1)}{2i({n - i})}\)
考虑我们只会从\(i\)转移到\(i + 1\)和\(i - 1\)两个状态,
其转移成功的概率比为成功条件下在状态空间中的数目占比,而考虑到\(i\)自身也有一个成功的条件概率,而且转移到两边的概率一样,所以固定系数为其。
然后直接对其高斯消元,发现其可以线性消元。
好毒瘤。
[MtOI2019]小铃的烦恼
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const int maxn = 2010;
string str;
double f[maxn][maxn], s[maxn], ans;
int num[30], n;
int main() {
cin >> str;
while(cin >> ans);
n = str.length();
for(int i = 0; i < n; i++) num[str[i]-'A']++;
for(int i = 1; i <= n-1; i++) {
f[i][i-1] = (double)(i-1) / (2*i); f[i][i] = -1;
f[i][i+1] = (double)(i+1) / (2*i); s[i] = -(double)n*(n-1)/(2*i*(n-i));
}
f[n][n] = 1; s[n] = 0;
for(int i = 1; i <= n-1; i++) {
if(fabs(f[i+1][i]) < eps) continue;
double z = f[i+1][i] / f[i][i];
for(int j = i; j <= n; j++) f[i+1][j] -= z * f[i][j];
s[i+1] -= z * s[i];
}
for(int i = n; i > 1; --i) {
if(fabs(f[i-1][i]) < eps) continue;
double z = f[i-1][i] / f[i][i];
for(int j = i; j <= n; j++) f[i-1][j] -= z * f[i][j];
s[i-1] -= z * s[i];
}
ans = 0;
for(int i = 0; i <= 'Z'-'A'; i++)
if(num[i])
ans += (double)num[i] / n * s[num[i]] / f[num[i]][num[i]];
printf("%.1f\n", ans);
return 0;
}
[BJOI2019]光线
考虑设\(f_i\)为透过第\(i\)块的,\(g_i\)为通过第\(i\)块反射回来的。
有\(f_i = a_i f_{i - 1} + b_i g_{i + 1}\)
\(g_i = b_i f_{i - 1} + a_i g_{i + 1}\)
发现\(g_n = b_i f_{n - 1}\)
\(f_n = a_i f_{n - 1}\)
考虑从后往前递推
然后得到系数表示从\(f_0\)往后乘一遍即可。
[PKUWC2018]猎人杀
考虑我们改变操作,每次一直开枪直到打到真人。
两种不同情况的操作,其概率不变。
我们考虑容斥。
设\(1\)之后死的人至少包含\(S\)里所有人的概率为\(p(S)\)
考虑子集反演。
那么答案为\(ans = \sum (-1)^|s|p(S)\)
设\(sum(S) =\sum_{i\in S}a_i\)
考虑如何求\(p(S)\)。
所以\(p(S) = \sum_{i = 0}^{\infty} (\frac{tot - a_1 - sum(S)}{tot})^i \frac{a_1}{tot}\)
等比数列求和得:\(p(S) = \frac{a_1}{a_1 + sum(S)}\)
考虑枚举 \(sum\)
所以有\(f(i) = \sum_{sum(S) = i}(-1) ^ |s|\)
考虑其为\((1 - x_i)\)的乘积。
直接就分治NTT可做。
小 Y 和恐怖的奴隶主
考虑我们直接暴力处理dp数组的概率。
表示其\(f_{(i,a,b,c)}\),\(i\)次攻击后,有\(a\)个1血仆从,\(b\)个2血仆从,\(c\)个3血仆从。
考虑其转移可以写作矩阵形式,其四维时后三维只有\(163\)个状态。
但是考虑多测,我们可以通过预处理\(2^i\)的矩阵乘积结果。
这样可以把多测时的\(n^3\)转为\(n^2\)。
提示我们注意数据范围,大部分数学题都有利用数据范围处理出暴力作法,最后通过某种算法将其复杂度优化到一种可接受的范围。
[NOI2019] 斗主地
捏马。怎么是被结论题打爆了。
猜测其期望仍旧是一个一次函数/二次函数。
如果写一个暴力\(dp\)的话,其实发现其值都是整数就很能说明问题了。
考虑处理系数,并暴力dp的方法处理前三项,再手动差值回来即可。
计数 与 求和
[HAOI2018]染色
考虑见到恰好我们直接冲二项式反演。
那么设至少有\(k\)个恰好\(S\)次的颜色为\(G(k)\)。
知\(G(k) = \binom{m}{k} * \prod^k \binom{n - i * s}{s} * (m - k) ^ {n - i * s}\)
考虑将中间\(\prod\)展开消元之后发现其为\(\frac{n!}{(s!)^k(n-i*s)!}\)
然后我们二项式反演回来\(F(k)=\sum (-1)^{i-k}\binom{i}{k}G(i)\)
这样就有了\(50\)分的好成绩。
[HAOI2018]染色
#include<bits/stdc++.h>
#define ll long long
#define M 10000005
#define mod 1004535809
int N,m,s;
int n;
ll si[M],inv[M];
int w[M];
inline ll Pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1)ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inline ll C(int x,int y){
if(y > x) return 0;
return si[x] * inv[y] % mod * inv[x - y] % mod;
}
ll F[M];
ll G[M];
ll ans = 0;
int main(){
scanf("%d%d%d",&N,&m,&s);
for(int i = 0;i <+ m;++i)
scanf("%d",&w[i]);
n = std::min(m,N / s);
si[0] = 1;
for(int i = 1;i < M;++i)
si[i] = si[i - 1] * i % mod;
inv[M - 1] = Pow(si[M - 1],mod - 2);
for(int i = M - 2;i >= 0;--i)
inv[i] = inv[i + 1] * (i + 1) % mod;
for(int i = 0;i <= n;++i){
F[i] = (C(m,i) * (si[N]) % mod * Pow(inv[s],i) % mod) * inv[N - s * i] % mod * Pow(m - i,N - s * i) % mod;
}
for(int i = 0;i <= n;++i)
for(int j = i;j <= n;++j){
G[i] = (G[i] + ((((j - i) % 2) ? (- 1) : 1) * C(j,i) + mod) % mod * F[j] % mod) % mod;
}
for(int i = 0;i <= n;++i)
ans = (ans + G[i] * w[i] % mod) % mod;
std::cout<<ans<<std::endl;
}
然后接下来是一个对二项式反演都通用的方式:\(NTT\) 减法卷积。
重新回看柿子:\(F(k)=\sum (-1)^{i-k}\binom{i}{k}G(i)\\=\sum (-1)^{i-k} \frac{i!}{(i - k)!k!}G(i)\)
\(\to k!F(k) = \sum \frac{(-1)^{i - k}}{(i - k)!}i!G(i)\)
变成了减法卷积的形式,于是我们可以在\(O(nlogn)\)中解决其。
[TJOI2019]唱、跳、rap和篮球
考虑二项式反演。
\(G(x) = \binom{n - 3x}{x}S(a - k,b - k,c - k,d - k,n - 4k)\).
其中\(S(a,b,c,d,n)\)为各项个数和总和随便排的数量。
考虑其等于四个带标号物品拼接,直接EGF即可。
然后反演过来。
\(O(nlog^2n)\)
[六省联考 2017] 组合数问题
知道背包就是卷积\((1 + x)\)。
然后发现答案即为\(\sum a_{j\mod k = i}\)知其直接循环卷积即可。
[六省联考 2017] 组合数问题]
#include<bits/stdc++.h>
#define ll long long
#define N 55
int n,k;
int p,r;
using std::vector;
vector<int> operator * (vector<int> &lhs,vector<int> &rhs){
vector<int>result(k);
for(int i = 0;i < k;++i)
for(int j = 0;j < k;++j)
result[(i + j) % k] = (result[(i + j) % k] + 1ll * lhs[i] * rhs[j]) % p;
return result;
}
int main(){
scanf("%d%d%d%d",&n,&p,&k,&r);
vector<int>a(k),ans(k);
if(k == 1)
a[0] = 2 % p;
else
a[0] = a[1] = 1;
ans[0] = 1;
ll len =1ll * n * k;
while(len > 0){
if(len & 1)
ans = ans * a;
a = a * a;
len >>= 1;
}
std::cout<<ans[r]<<std::endl;
}
[THUPC2021 初赛] 方格游戏
考虑其答案等于无障碍的点两两间最短距离和加上绕远路的和。
考虑前者可以容斥计算。
后者考虑上下绕远路与左右绕远路。
以左右绕远路来说,其在竖坐标上贡献的答案为在其竖坐标区域内的点的竖坐标到其上下两边最短距离。
上下同理。
[HAOI2018]苹果树
不看数据范围失败人。
考虑生成树的个数为\(n!\)个。
那现在等同于求所有方案的权值和。
对一颗生成树来说转成每个点底下的一颗子树大小乘全局其他点。
那考虑枚举\(i\)底下的一边的子树的大小,然后计算其出现的次数即可。
那么考虑从大到小加,那么我们操作到\(i\)个节点,则有\(i!\)种情况。
考虑枚举一边子树大小\(j\),那么子树无关,有\(j!\)情况,由于子树带标号\(\binom{n - i}{j}\)
所以当操作到\(i\)时,有\(i+1\)个位置可放,由于我们强制枚举了一边,所以还有\(i\)个位置,每次多加一个点会多一个位置。所以剩下\((n - i - j)\)个的方案为\(\prod_{i}^{n - j -1}k\)
直接\(O(n^2)\)计算即可。
由于无逆元,所以需要\(O(n^2)\)计算组合数及\(\prod_{i}^{n - j -1}k\)。
[HAOI2018]苹果树
#include<bits/stdc++.h>
#define ll long long
#define N 2005
int n,mod;
ll c[N][N];
ll s[N][N];
ll ans = 0;
int main(){
scanf("%d%d",&n,&mod);
c[0][0] = 1;
for(int i = 1;i <= n;++i)
for(int j = 0;j <= n;++j){
c[i][j] = (c[i - 1][j] + (j != 0 ? c[i - 1][j - 1] : 0)) % mod;
}
for(int i = 1;i <= n;++i){
s[i][i - 1] = 1;
for(int j = i;j <= n;++j)
s[i][j] = s[i][j - 1] * j % mod;
}
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n - i;++j){
ans = (ans + 1ll * 2 * j * (n - j) % mod * s[1][i] % mod * s[1][j] % mod * c[n - i][j] % mod * s[i][n - j - 1] % mod) % mod;
}
std::cout<<ans<<std::endl;
}
[省选联考 2020 A 卷] 组合数问题
\((\sum_{k = 0}^{n - i}f(k)(x^k)\binom{n}{k}\)
有好性质\(\binom{n}{m}k^{\underline m} = \binom{n - k}{m - k}n^{\underline m}\)
考虑把多项式写作下降幂形式。
不妨写作\(f(x) = \sum_{i = 0}^m b_i x^{\underline i}\)
那么有\(LHS = \sum_{i = 0}^m b_i n^{\underline i}\sum _{k = 0}^n\binom{n - i}{k - i}x^k\)
考虑 \(k - i > 0\) 才有值,考虑改成枚举\(k - i\)
那么有\(LHS = \sum_{i = 0}^m b_i n^{\underline i}\sum _{k = 0}^n\binom{n - i}{k}x^{k + i} = \sum_{i = 0}^mb_in^{\underline i}x^i\sum_{k = 0}^{n - i}\binom{n - i}{k}x^k\)
发现后者可写作\((x + 1)^{n - i}\)
所以有\(\sum_{i = 0}^m b_i n^{\underline i}x^i(x + 1)^{n - i}\)
于是问题转成普通多项式转下降幂多项式。
因为有\(x^n = \sum_{i = 0}^{n}\begin{Bmatrix}n\\i\end{Bmatrix}x^{\underline i}\)
所以知\(b_i = \sum_{j = i}^m\begin{Bmatrix}j\\i\end{Bmatrix}a_j\)
直接\(O(m^2)\)递推第二类斯特林数,总时间复杂度\(O(m^2)\)。
[省选联考 2020 A 卷] 组合数问题
#include<bits/stdc++.h>
#define ll long long
#define N 1005
ll S[N][N];
ll mod;
ll n,x,m;
ll b[N];
ll a[N];
inline ll Pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
ll under;//n^{\underline i}
ll xi;//x^i
ll ans = 0;
int main(){
scanf("%lld%lld%lld%lld",&n,&x,&mod,&m);
for(int i = 0;i <= m;++i)
scanf("%lld",&a[i]);
S[0][0] = 1;
for(int i = 1;i <= m;++i)
for(int j = 1;j <= i;++j)
S[i][j] = (S[i - 1][j - 1] + j * S[i - 1][j] % mod) % mod;
for(int i = 0;i <= m;++i)
for(int j = i;j <= m;++j)
b[i] = (b[i] + S[j][i] * a[j] % mod) % mod;
under = 1,xi = 1;
for(int i = 0;i <= m;++i)
ans = (ans + b[i] * under % mod * xi % mod * Pow(x + 1,n - i) % mod) % mod,under = (under * (n - i)) % mod,xi = xi * x % mod;
std::cout<<ans<<std::endl;
}
[SNOI2019]数论
考虑枚举\(a_i\),然后查询有多少个贡献。
考虑对\((i,(i + P)\bmod Q)\)连边。
则在\(Q\)域下其若干环。
考虑对每个环处理前缀和。
考虑整环以及不完全的操作即可。
[Cnoi2019]最终幻想
\(f_n(k) = \begin{cases}\sum_{i = 0}^{k - 1}f_{n - 1}(i) + 1\\k + 1&n = 1\end{cases}\)
考虑生成函数
\(G_n(x) = \sum_{k = 0}^{\infty} f_n(k)x^k\)
考虑先计算\(G_1\)
\(G_1(x) = \sum_{x = 0}^{\infty} f_1(k)x^k \\= \sum (k + 1) x^k\\=(\sum x^{k+1})'\\=(\sum_{x = 1}x^{k + 1})'\\= (\sum x^k - 1)'\\= \frac{1}{(1-x)^2}\)
\(n > 1\)时
\(G_n(x) = \sum f_n(k)x^k\\=\sum(\sum_{i = 0}^{k - 1}f_{n - 1}(i) + 1)x^k\\=\frac{1}{1- x} + \frac{x}{1 - x} G_{n - 1}(x)\)
所以有\(G_n(x) = \frac{x^{n - 1}}{(1 - x) ^ {n + 1}} + \sum_{i = 0}^{n - 2} \frac{x^i}{(1- x)^{i + 1}}\)
考虑直接猛推柿子得\(= \frac{1}{1 - 2x} - \frac{1}{1 - 2x}\frac{x^{n+1}}{(1-x)^{n + 1}}\)
所以知:
\(f_n(x) = \begin{cases}2^k&k\leq n\\2^k - \sum^{k - n -1}_{0}C^{n}_{n + 1}2^{k - n - 1}&k > n\end{cases}\)
CF662C Binary Table
被板板题教育了。
考虑记\(m\)行里的状态为\(S\)的数量为\(S_i\),考虑枚举翻转的状态为\(X\),翻转后为\(Y_i\),那么有\(S_i \oplus X = Y_i\),那么有\(S_i \oplus Y_i = X\),其翻转为的\(Y_i\)的状态的答案为\(F_i\)。
那么有\(Ans[X] = \sum_{Y \oplus S = X} F_Y \times Q_s\)
然后可以处理异或卷积。
CF662C Binary Table
#include<bits/stdc++.h>
#define ll long long
#define N ((int)(1ll << 20) + 10)
ll F[N],Q[N];
int n,m;
int a[25][100005];
#define lowbit(x) (x & -x)
inline int cnt(ll s){
int ans = 0;
while(s){
s -= lowbit(s);
ans ++ ;
}
return ans;
}
inline void FWT(ll *f,int type){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i){
ll x = f[i],y = f[i + mid];
f[i] = (x + y) * (type == 1 ? 1 : 0.5);
f[i + mid] = (x - y) * (type == 1 ? 1 : 0.5);
}
}
ll Ans[N];
ll minn;
int main(){
scanf("%d%d",&n,&m);
minn = n * m;
for(int i = 1;i <= n;++i)
for(int j = 1;j <= m;++j)
scanf("%1d",&a[i][j]);
for(int i = 1;i <= m;++i){
ll s = 0;
for(int j = 1;j <= n;++j){
s = s + (a[j][i] << (j - 1));
}
Q[s] ++ ;
}
for(int i = 0;i < (1ll << n);++i)
F[i] = std::min(cnt(i),n - cnt(i));
n = (1ll << n);
FWT(F,1);
FWT(Q,1);
for(int i = 0;i < n;++i)
Ans[i] = F[i] * Q[i];
FWT(Ans,-1);
for(int i = 0;i < n;++i)
minn = std::min(minn,Ans[i]);
std::cout<<minn<<std::endl;
}
[SDOI2018]反回文串
一直在想怎么算好的串,于是寄寄寄。
考虑如何计算坏的串,考虑一个回文串可以转置出其对应循环节个串。
但是发现这样会算重,因为一个回文串可能会转出其他不同的回文串。
发现这种情况只会出现一次,于是我们让偶数串只贡献其\(\frac{1}{2}\)的循环节。
所以答案为\(ans = \sum_{d|n} f(d) h(d)\)
\(f(d)\)为循环节为\(d\)的回文串个数。
\(h(d)\)为奇偶系数。
设\(g(n)\)为长度为\(n\)的回文串的总个数,枚举循环节,则\(g(n) = \sum_{d|n} f(d) \to f(n) = \sum_{d|n} \mu(\frac{n}{d})g(d)\)
\(Ans = \sum_{d|n}\sum_{l|d}\mu(\frac{d}{l})g(l) = \sum_{l|n}g(l)\sum_{tl|n}h(tl)\mu(t)\)
考虑\(\sum_{t | \frac{n}{l}}\mu(t)h(tl) = 0\)
所以有\(Ans = \sum_{l|n}g(l)h(l)\sum_{hl|n}t\mu(t)\)
依照生成函数的知识知\(\sum_{tl|n}t\mu(t) = \prod(1-p_i)\)
所以直接\(pollard\ rho\)即可。
前者直接\(O(d(n))\)枚举因子即可
【UNR #2】黎明前的巧克力
考虑答案实际上是异或和为\(0\)的集合的\(\sum 2^{|S|}\)。
考虑每加入一个即有一个两倍的贡献。
考虑其背包问题我们可以使用卷积优化,这里不过是把背包问题的加法取做了\(\oplus\),我们同样可以使用异或卷积处理其。
实际上即求\(\oplus_{i = 1}^i (1 + 2x^{a_i})\)的第\(0\)项系数。
思考如何处理其。
重新回顾FWT的过程。
\(FWT(A)_i = \sum_{popcnt(i \& j) \bmod 2} A_j - \sum_{popcnt(i \& j) \bmod 2 \oplus 1} A_j\)
所以对\((1 + 2x^{a_i})\)的\(FWT\)的点值表示只有\((-1,3)\)两种值。
由于和的\(FWT\)等同于\(FWT\)的和。
又有对于每一位\(cnt(3) + cnt(-1) = n\),我们又有\(sFWT_i = 3*cnt(3) - cnt(-1)\)
可以解得\(cnt(3)\)与\(cnt(-1)\),还原乘积\(FWT_i = 3^{cnt(3)}(-1)^{cnt(-1)}\)
最后对其\(IFWT\)回来即可。
【UNR #2】黎明前的巧克力
#include<bits/stdc++.h>
#define ll long long
#define N ((int)(1ll << 20) + 10)
#define mod 998244353
#define inv2 499122177
ll F[N],Q[N];
int n,m;
inline ll Pow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1)ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inline void FWT(ll *f){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i){
ll x = f[i],y = f[i + mid];
f[i] = (x + y);
f[i + mid] = (x - y) ;
}
}
inline void IFWT(ll *f,int type){
for(int mid = 1;mid < n;mid <<= 1)
for(int block = mid << 1,j = 0;j < n;j += block)
for(int i = j;i < j + mid;++i)
{
ll x = f[i],y = f[i + mid];
f[i] = (x + y) % mod * (type == 1 ? 1 : inv2) % mod;
f[i + mid] = (x - y + mod) % mod * (type == 1 ? 1 : inv2) % mod;
}
}
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;++i){
int x;
scanf("%d",&x);
F[0] = (F[0] + 1) % mod;
F[x] = (F[x] + 2) % mod;
}
m = n;
n = (1ll << 20);
FWT(F);
for(int i = 0;i < n;++i){
int cnt = (3 * m - F[i]) / 4;
Q[i] = (cnt % 2) ? (mod - Pow(3,m - cnt) % mod) : (Pow(3,m - cnt));
}
IFWT(Q,-1);
std::cout<<(Q[0] - 1 + mod) % mod<<std::endl;
}
[十二省联考 2019] 皮配
哈...哈...什么时候能看对题一次呢。
考虑\(O(nM^2)\)的暴力,设黄色与圆粒的重量和,则可以做到\(50pts\)。
考虑\(k = 0\):所有的豆子都无限制,考虑将豆子进行划分,发现无论是划分黄/绿还是划分圆/皱都不影响,考虑分开计算。
设\(f_i\)为黄色和为\(i\)的方案数,\(g_i\)圆粒和的为\(i\)的方案数,可以\(O(nM)\)求得。
那么此时答案为 \(\sum_{i = S - C_1}^{C_0} \sum_{j = S - D_1}^{D_0}f_ig_j\)
这样拼起来有\(70pts\)。
考虑挑剔的豆子称作有毒。
带有有毒豆子的豆荚为有毒的豆荚。
考虑先对无毒的豆荚求\(f\)。
考虑对无毒的豆子求\(g\)。
接下里只要考虑对有毒的豆子操作即可,其操作一定会带动整个豆荚操作。
于是考虑对其做\(50pts\)的暴力\(F\)即可。
最后对其合并即可。
复杂度\(O((c+n)M + k^2sM)\)
反演
[SDOI2014]数表
直接反演可得 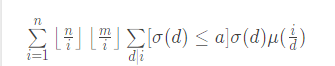
考虑把询问对\(a\)排序依次对后缀操作,用BIT维护即可。
[HEOI2016/TJOI2016]求和
\(\sum_{i = 0}^n\sum_{j = 0}^n S_i^j 2^j j!\)
\(\sum_{j = 0}^n2^jj!\sum_{i = 0}^nS^j_i\)
\(S_n^m = \sum\frac{(-1)^k(j - k)^i}{k! (j - k)!}\)
所以\(\sum 2^j j! \sum_{i = 0}\sum_{k = 0}^j\frac{(-1)^k(j - k)^i}{k! (j - k)!} = \sum 2^j j! \sum_{k = 0}^j\frac{(-1)^k\sum_{i = 0}^n(j - k)^i}{k!(j - k)!}\)
可以NTT做。
所以发现这个做法可以扩展\(2^j j!\)至任意可快速求值的系数。