Desctiption
洛谷
AcWing
Solution
Solution 1 (30pts)
我们可以根据输入的后缀表达式建立一棵表达式二叉树,其中所有的元素为叶子节点,符号为其他节点,每次暴力修改该点到根节点路径的值。
对于如何转为表达式二叉树,可以使用一个栈来处理。
时间复杂度最坏 (O(nq))。
Solution 2 (100pts)
观察题面,会发现有一行字:每个变量在表达式中出现恰好一次。所以每个我们可以发现:每个数对于根节点值的改变仅有两种可能:改变或者不改变。
先预处理出在没有节点取反的情况下,每个节点的值(包括叶子节点),这个用一遍 DFS 就行。
再分析一下三种符号的性质:
-
! 取反,它的儿子只会有一个。只要出现了,以它为根的子树只要变化,会对这个节点造成影响。
-
& 与,有两个儿子节点。如果有儿子结点值为 (0),因为
0 & x = 0,所以另一个儿子节点不管怎么变,都不会对答案造成影响,只要搜索这个为0的子树。 -
| 或,有两个儿子结点。如果有儿子结点值不为 (0),因为
x | 0 = 1,所以另一个儿子节点为不为0也没关系,不管怎么变,都不会对答案造成影响,只要搜索这个不为0的子树。
举个例子助理解:
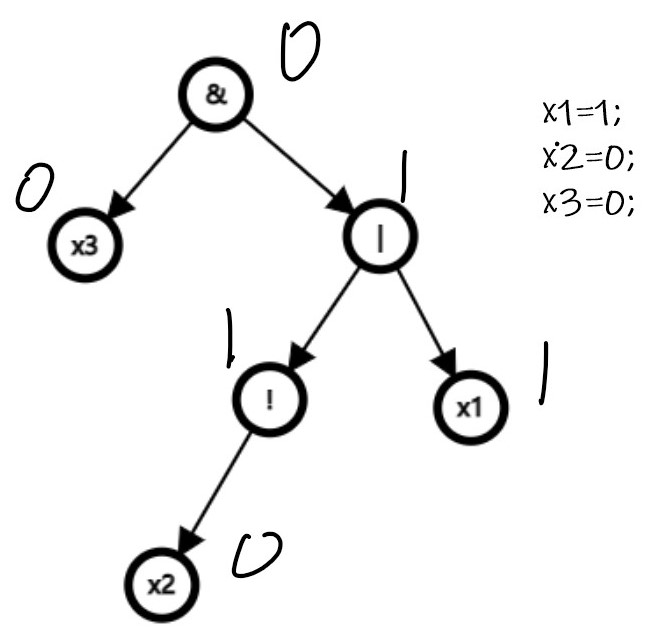
这是一棵表达式树。可以看出,如果我们对 (x2) 取反,由于 (x3 = 0),所以最后根节点的答案不会改变,不受影响,这个点没有用。
但是如果对 (x3) 取反,则会出现 1 & 1 = 1,对答案发生改变,这个点是有用的。
所以我们引入一个“有用标记”数组,表示第 (i) 号节点如果取反会不会对根节点(答案)造成影响, 每次到达一个节点,向下搜索会对这个节点造成影响的儿子节点,最后能到达的所有叶子节点就是有用的节点。
最后查询时直接判断这个点是不是有用的,有用就把答案取反即可。
时间复杂度为 (O(n+q)),通过。
关于如何存储一个字符型的节点,我们可以在 (n) 个点的基础上增开一些点,点的编号从 (n+1) 开始,这些点向原来的点连边即可。
这题主要是细节处理较多,主要看代码。
Code
// by youyou2007 Aug.
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <queue>
#include <stack>
#define REP(i, x, y) for(register int i = x; i < y; i++)
#define rep(i, x, y) for(register int i = x; i <= y; i++)
#define PER(i, x, y) for(register int i = x; i > y; i--)
#define per(i, x, y) for(register int i = x; i >= y; i--)
#define lc (k << 1)
#define rc (k << 1 | 1)
using namespace std;
const int N= 1E6 + 5;
string s;
int n, a[N], w[N], f[N], cnt;
vector <int> g[N];
stack <int> sta;//运用栈来解后缀表达式。
int opt[N], q;
int dfs(int x)//第一次搜索,计算出每个节点的值。
{
if(x <= n) return a[x];//这里用了一个技巧,就是叶子节点的编号都是小于n的
if(opt[x] == 1)//如果为取反
{
int y = g[x][0];
int temp = !dfs(y);//则向下搜索,取反儿子的值
return w[x] = temp;
}
else if(opt[x] == 2)//如果为与
{
int temp = 1;//计算中初始值要注意!
for(int i = 0; i < g[x].size(); i++)//向下搜索,把两个儿子结点的值进行与操作
{
int y = g[x][i];
temp = temp & dfs(y);
}
return w[x] = temp;
}
else if(opt[x] == 3)//或操作,同理
{
int temp = 0;
for(int i = 0; i < g[x].size(); i++)
{
int y = g[x][i];
temp = temp | dfs(y);
}
return w[x] = temp;
}
}
void dfs2(int x)
{
if(x <= n)//如果搜到了叶子节点
{
f[x] = 1;//置有用
return;
}
if(opt[x] == 1)//如果该节点是取反,那么肯定有用
{
int y = g[x][0];
dfs2(y);
}
else if(opt[x] == 2)//如果是与运算
{
int y1 = g[x][0];
int y2 = g[x][1];
// cout << y1 << " " << y2 << " " << w[y1] << " "<< w[y2]<<endl;
if(w[y1] == 1) dfs2(y2);//有儿子的值为1,则搜另一个儿子
if(w[y2] == 1) dfs2(y1);//注意,这里并不是else if! 因为有可能两个儿子节点都是1!
}
else if(opt[x] == 3)//和与运算同理
{
int y1 = g[x][0];
int y2 = g[x][1];
if(w[y1] == 0) dfs2(y2);
if(w[y2] == 0) dfs2(y1);
}
}
int main()
{
getline(cin, s);
scanf("%d", &n);
rep(i, 1, n)
{
scanf("%d", &a[i]);
w[i] = a[i];//每个叶子节点的值就是a数组的值,要赋上
}
int len = s.length();
cnt = n;//cnt就是对字符另建节点
rep(i, 0, len - 1)//将字符串转为表达式树
{
if(s[i] == ' ') continue;
else if(s[i] == 'x')
{
int temp = 0;
i++;
while(s[i] >= '0' && s[i] <= '9')
{
temp = temp * 10 + s[i] - '0';
i++;
}
sta.push(temp);
}
else if(s[i] == '!')
{
opt[++cnt] = 1;
int temp = sta.top();
sta.pop();
g[cnt].push_back(temp);//连边
sta.push(cnt);
}
else if(s[i] == '&' || s[i] == '|')
{
if(s[i] == '&') opt[++cnt] = 2;
if(s[i] == '|') opt[++cnt] = 3;
int temp1 = sta.top(); sta.pop();
int temp2 = sta.top(); sta.pop();
g[cnt].push_back(temp1);
g[cnt].push_back(temp2);
sta.push(cnt);
}
}
int ans = dfs(sta.top());//初始答案就是根节点的值
memset(f, 0, sizeof f);
// rep(i, 1, cnt) cout << w[i] << " ";
// cout << endl;
dfs2(sta.top());//进行第二遍的打“有用标记操作”
scanf("%d", &q);
while(q--)
{
int xx;
scanf("%d", &xx);
if(!f[xx]) printf("%d
", ans);//如果有用就是取反,没用就原样输出
else printf("%d
", !ans);
}
return 0;
}