题意:一个二进制矩阵是好的,当且仅当所有长度为偶数的矩阵的1的个数为奇数。给定一个n行m列的矩阵a,决定最小要改变的次数,使得这个矩阵变好。
分析:(1 <= n <= m <= 1e6并且n * m <= 1e6),输入范围的m >= n。我们先考虑长度为2的子矩阵,4个2 * 2的子矩阵可以拼成一个4 * 4的子矩阵,可以发现,奇数 * 4 = 偶数,那么这个4 * 4的子矩阵就不合法了,因此,我们只需要考虑长度为2或3的子矩阵,再看输入范围m >= n,因此我们只需要考虑n是否 > 3,如果 > 3,则输出-1,当n = 1的时候,我们输出0即可,不需要改变。然后,我们开始考虑动态规划求解最少的改变次数,我们可以一列一列地转移,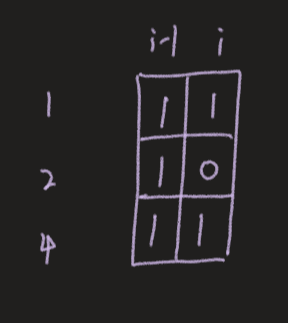 。假设第i列填的数字从上到下是1 0 1,那么前面一列的第一个数字如果是1的话,那么前面一列可以填111,那么其中的2个2 * 2的矩阵就有奇数个1,上一列的状态就可以转移到当前列,我们用数字存储,上一列是7,当前列是5,那么7--->5就是可以合法转移的,同样5--->7也是可以合法转移的,我们可以采用第一位 * 1 + 第二位 * 2 + 第三位 * 4的方式存储状态。我们可以预处理出这些状态之间是否可以转移,可以看代码,即统计每个子矩阵中1的个数,然后判断即可。之后我们再考虑如果设计DP状态,我们可以采用f[i][msk]的方式,即处理了前i列,第i列的二进制串的状态是msk的数字,我们可以从f[i - 1][premsk]转移过来,只要msk可以从premsk转移过来,然后我们就可以写出状态转移方程了,f[i][msk] = min(f[i][msk], f[i - 1][premsk] + cost),这个常数cost是我们的原先矩阵的当前列改成msk的次数,我们可以通过(mskoplus)原先列,然后统计这个异或值的1的个数即可。
。假设第i列填的数字从上到下是1 0 1,那么前面一列的第一个数字如果是1的话,那么前面一列可以填111,那么其中的2个2 * 2的矩阵就有奇数个1,上一列的状态就可以转移到当前列,我们用数字存储,上一列是7,当前列是5,那么7--->5就是可以合法转移的,同样5--->7也是可以合法转移的,我们可以采用第一位 * 1 + 第二位 * 2 + 第三位 * 4的方式存储状态。我们可以预处理出这些状态之间是否可以转移,可以看代码,即统计每个子矩阵中1的个数,然后判断即可。之后我们再考虑如果设计DP状态,我们可以采用f[i][msk]的方式,即处理了前i列,第i列的二进制串的状态是msk的数字,我们可以从f[i - 1][premsk]转移过来,只要msk可以从premsk转移过来,然后我们就可以写出状态转移方程了,f[i][msk] = min(f[i][msk], f[i - 1][premsk] + cost),这个常数cost是我们的原先矩阵的当前列改成msk的次数,我们可以通过(mskoplus)原先列,然后统计这个异或值的1的个数即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 8;
const int M = 1000005;
const int inf = 0x3f3f3f3f;
char tmp[M];
int cnt[N];
int g[3][M];
bool ok2[N][N];
bool ok3[N][N];
int dp2[M][N];
int dp3[M][N];
int n, m;
void init2()
{
for(int msk = 0; msk < 4; ++msk)
for (int premsk = 0; premsk < 4; ++premsk)
{
int tot = cnt[msk] + cnt[premsk];
if (tot % 2 == 1)
ok2[premsk][msk] = ok2[msk][premsk] = true;
}
}
void init3()
{
for(int msk = 0; msk < 8; ++msk)
for (int premsk = 0; premsk < 8; ++premsk)
{
int cnt1 = ((msk >> 0) & 1) + ((msk >> 1) & 1) + ((premsk >> 0) & 1) + ((premsk >> 1) & 1);
int cnt2 = ((msk >> 1) & 1) + ((msk >> 2) & 1) + ((premsk >> 1) & 1) + ((premsk >> 2) & 1);
if (cnt1 % 2 == 1 && cnt2 % 2 == 1)
ok3[premsk][msk] = ok3[msk][premsk] = true;
}
}
void solve3()
{
int a = g[0][1] * 1 + g[1][1] * 2 + g[2][1] * 4;
for (int msk = 0; msk < 8; ++msk)
{
int cost = cnt[a ^ msk];
dp3[1][msk] = cost;
}
for (int i = 2; i <= m; ++i)
{
int a = g[0][i] * 1 + g[1][i] * 2 + g[2][i] * 4;
for (int msk = 0; msk < 8; ++msk)
{
dp3[i][msk] = inf;
for (int premsk = 0; premsk < 8; ++premsk)
{
if (!ok3[premsk][msk]) continue;
int cost = cnt[a ^ msk];
dp3[i][msk] = min(dp3[i][msk], dp3[i - 1][premsk] + cost);
}
}
}
}
void solve2()
{
int a = g[0][1] * 1 + g[1][1] * 2;
for (int msk = 0; msk < 4; ++msk)
{
int cost = cnt[a ^ msk];
dp2[1][msk] = cost;
}
for (int i = 2; i <= m; ++i)
{
int a = g[0][i] * 1 + g[1][i] * 2;
for (int msk = 0; msk < 4; ++msk)
{
dp2[i][msk] = inf;
for (int premsk = 0; premsk < 4; ++premsk)
{
if (!ok2[premsk][msk])continue;
int cost = cnt[a ^ msk];
dp2[i][msk] = min(dp2[i][msk], dp2[i - 1][premsk] + cost);
}
}
}
}
int main()
{
for(int i = 0; i < N; ++i)
for (int j = 0; j < 3; ++j)
{
if ((i >> j) & 1) ++cnt[i];
}
init2();
init3();
cin >> n >> m;
if (min(n, m) == 1)
{
puts("0");
return 0;
}
else if (min(n, m) > 3)
{
puts("-1");
return 0;
}
else
{
for (int i = 0; i < n; ++i)
{
scanf("%s", tmp + 1);
for (int j = 1; j <= m; ++j)
g[i][j] = tmp[j] - '0';
}
if (n == 2)
{
solve2();
int res = inf;
for (int i = 0; i < 4; ++i)
res = min(res, dp2[m][i]);
printf("%d
", res);
}
else
{
solve3();
int res = inf;
for (int i = 0; i < 8; ++i)
res = min(res, dp3[m][i]);
printf("%d", res);
}
}
return 0;
}