POJ-3304 Segments(判断直线和线段的相交)

题意:给定n条在二维平面上的线段，写一个程序，判断是否存在一个直线，使得所有的线段投影到这根直线上，至少存在一个公共点。

分析:从侧面考虑，如果存在一根直线，使得所有线段到这根直线上的投影至少有一个公共点，那么对所有投影的交集区域做一根垂线，可以穿过所有的线段。从而转换为找到一根直线，使得这根直线可以穿过所有线段的问题。对这根直线摆动，只要不超过任何一条线段的端点即可，然后摆动到不能摆动为止，会发现处于这条直线的端点两侧可以固定下来，所以我们可以枚举线段的任意两个端点作为一根直线，然后判断是否每一根线段的两个端点都在这根直线的两侧，这个可以用叉积判断。

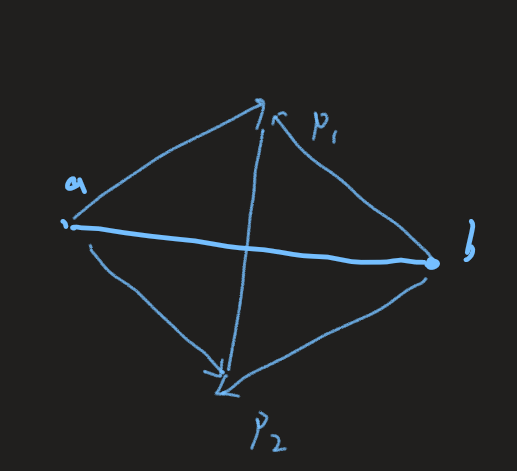
只要线段的两个端点到直线的两侧端点的向量叉乘相乘 <= 0即可，((vec{ap1} imesvec{ap2} * vec{bp1} imesvec{bp2}))，叉乘的两个向量具有符号，< 0表示在一根直线的左侧，> 0表示在一根直线的右侧，只要两个相乘 < 0即可。==0的情况表示这根线段在这根直线上，还有就是枚举的直线需要判断是否为一个点，这是一个特殊情况。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;
//两个点之间的距离<1e-8就表示相等
const double eps = 1e-8;

int dcmp(double x)
{
	if (fabs(x) < eps) return 0;
	else return x < 0 ? -1 : 1;
}

struct Point
{
	double x, y;
	Point(double x = 0, double y = 0) : x(x), y(y) {}
};

typedef Point Vector;

//向量 + 向量 = 向量， 点 + 向量 = 点
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }

//点 - 点 = 向量
Vector operator - (Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }

//向量 * 标量 = 向量
Vector operator * (Vector A, double p) { return Vector(A.x * p, A.y * p); }

//向量 / 数 = 向量
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y / p); }

bool operator<(const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) < 0 || dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) < 0;
}

bool operator == (const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}

double Dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
//求A的单位法线，垂直于A
Vector Normal(Vector A)
{
	double L = Length(A);
	return Vector(-A.y / L, A.x / L);
}

struct Line{
	Point p;
	Vector v;
	Line(Point p, Vector v) :p(p), v(v) { }
	//直线上的点坐标
	Point point(double t) {
		return p + v * t;
	}
	//平移直线d距离
	Line move(double d) {
		return Line(p + Normal(v) * d, v);
	}
};

const int N = 105;
Point a[N], b[N];
Point c[2 * N];

bool check(Point q1, Point q2, Point a, Point b)
{
	Vector bq1(q1 - b);
	Vector bq2(q2 - b);
	Vector aq1(q1 - a);
	Vector aq2(q2 - a);
	if (dcmp(Cross(bq1, bq2) * Cross(aq1, aq2)) <= 0) return true;
	return false;
}

int main()
{
	int t;
	scanf("%d", &t);

	while (t--)
	{
		int n;
		scanf("%d", &n);

		for (int i = 1; i <= n; ++i)
		{
			scanf("%lf%lf%lf%lf", &a[i].x, &a[i].y, &b[i].x, &b[i].y);
			c[i].x = a[i].x, c[i].y = a[i].y, c[i + n].x = b[i].x, c[i + n].y = b[i].y;
		}

		bool f = false;
		//枚举任意两个端点
		for(int i = 1; i <= 2 * n; ++i)
			for (int j = i + 1; j <= 2 * n; ++j)
			{
				Point q1(c[i].x, c[i].y);
				Point q2(c[j].x, c[j].y);
				if (q1 == q2) continue;
				bool flag = true;
				for (int k = 1; k <= n; ++k)
				{
					if (!check(q1, q2, a[k], b[k]))
					{
						flag = false;
						break;
					}
				}
				if (flag)
				{
					f = true;
					break;
				}
			}
		if (f) puts("Yes!");
		else puts("No!");
	}

	return 0;
}