卡尔曼滤波（kalman）相关理论以及与HMM、最小二乘法关系

一、什么是卡尔曼滤波

　　在雷达目标跟踪中，通常会用到Kalman滤波来形成航迹，以前没有学过机器学习相关知识，学习Kalman时，总感觉公式看完就忘，而且很多东西云里雾里并不能深入理解，最后也就直接套那几个递推公式了。通过上一篇CRF，我们可以顺便回顾一下HMM，事实上，这几种算法和Kalman之间是有联系的，这个联系，据说是在PRML这本书的第13章里讲的线性动态系统（LDS）讲的，有机会一定好好拜读一下！那么什么是Kalman滤波呢？

　　首先，简单的理解就是：对于一个目标，它会具有一定的速度，如果是机动的，还会有加速度，不过这都不重要，重要是的，这个目标各个时刻的位置是我们需要关心的。对于目标的找寻，尊寻方程：

X(k)=A X(k-1)+B U(k)+W(k)               状态方程

Z(k)=H*X(k)+V(k)                               量测方程

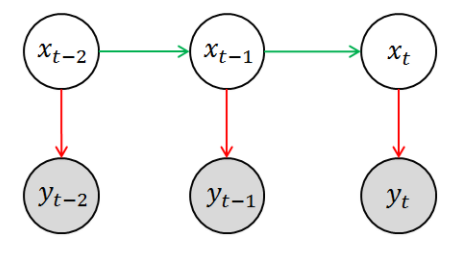
　　卡尔曼滤波用到的线性离散状态和观测方程则如上，A表示的是状态转移矩阵，H表示的是观测矩阵，W和V都是满足高斯白噪声的分布，并且W和V是独立的，即E{w*v^T} = 0。而Kalman滤波的总体思路就是，我们用k-1时刻的估计值X^{^}去预测k时刻的Z，然后用预测的值和实际观测到的值进行比对，用误差修正k+1时刻的估计方法。其实讲到这里，可以回顾HMM模型，看以看到，模型中白圈代表了状态，而蓝圈代表了观测值，因此，可以看到Kalman和HMM其实是有一定的联系的。

 二、Kalman和HMM之间的关系

　　其实，讲到这里，我就想说一下我理解的Kalman与HMM的关系，事实上，他们解决的问题模型都是如上图所示，只不过一个是利用最小均方误差准则进行估计，一个是利用最大后验进行估计。事实上，HMM的预测问题中，就是一个最大的后验概率作为其似然函数，然后通过viterbi算法解的这个似然函数。

　　参考：参数估计     、  HMM

 　　当然上面都是我的私货，比较标准的答案：《Advanced Digital Signal Processing and Noise Reduction 4th Edition》

　　稍微翻译下：

　　相同点：

• 马尔科夫性：两种都是基于马尔科夫过程，当前时刻的状态只与上一时刻有关系，譬如，当前时刻的位置只与上一时刻的位置有关；
• 高斯观测：两者的量测值都符合高斯分布；

　　不同点：

• 状态的连续性：Kalman的状态是连续值，而HMM的状态是可数的（类似于一个是线性回归、一个是逻辑回归，或者说一个是回归问题、一个是分类问题）；
• 马尔科夫状态模型：Kalman用状态转移矩阵+高斯的过程噪声演化马尔科夫过程，而HMM只有状态转移矩阵；
• 隐藏层状态：Kalman的隐状态由于噪声的原因不可观察，而HMM由于隐层状态的转化没有噪声，也就是说，由观测值可推断HMM的隐藏层的状态，但是不能推断Kalman的状态究竟是哪一个；

　　　　　　

 三、Kalman滤波公式

　　事实上，Kalman滤波的递推公式并不复杂，只要真正理解了最小均方误差估计，其递推公式就很好掌握了。

　　首先是最基本的两个方程：

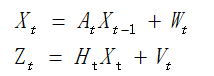
　　W符合N（0，Q），V符合N（0，R）。

　　然后可以看到，Kalman滤波的五个基本的滤波方程：

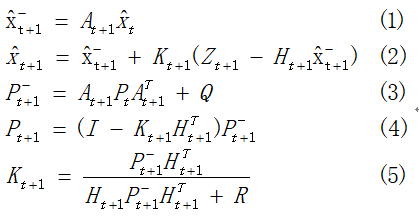
　　对于这个方程组的推导：

　　证明到这里，可以看到，上面的式子是由公式（2）得到的。公式（2）包含一个新的定义：新息，实际上就是量测值与预测值的差嘛，在我们这个kalman滤波中，它反映了过程噪声和测量噪声综合对测量状态值的影响，即w和v两者共同作用于新息的影响。假设一个数值c由两部分内容a和b组成，通常两者关系的表达方法有两种：相加和比重。

• c = a+b（相加）
• a = n*c   ;  b = (1-n)*c  （比重）

　　这样的话，公式（2）中，如果我们想要得到归于状态转移的影响，则可以用a = n*c来表示，n就是式子中的K（被称为卡尔曼增益）。

　　如上公式，表示估计值与实际值之间的差，根据最小均方误差准则，应该是E(e^2)最小。

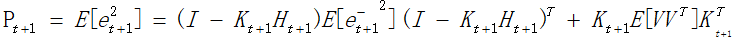
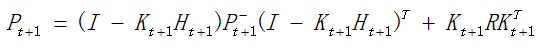
　　然后，可以简单的推导一下其中的K的求法

　　求：

　　由于：

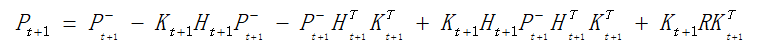
　　求导得到：

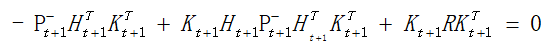
　　求得K，如公式（5）所示：

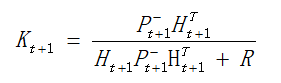
　　事实上，对于上面求P_t+1的 公式和求导公式两者结合，可以消除0项，即化简得到公式（4）.

　　以上即为Kalman滤波公式的简单推导过程。

 四、α-β滤波器

　　如上根据Kalman滤波的递推公式，可以看到，为了求卡尔曼增益，消耗了大部分的工作量，为了减少计算量，必须改变增益矩阵的计算方法，因此人们提出了常增益滤波器，此时的增益的计算不再与协方差有关系，因而，可以在滤波过程中离线计算卡尔曼增益，这样就大大减少了计算量，有利于工程实现。α-β滤波器是针对匀速运动目标模型的一种常增益滤波器。

　　α-β滤波器主要针对的是匀速运动目标模型，目标模型的状态向量只包含位置和速度两项。其增益表现如下：

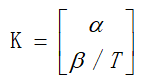
　　其中，α、β为无量纲的值，分别为目标状态的位置和速度分分量的常滤波增益，其中T为采样间隔。对于具体的取值，可以通过《雷达数据处理及应用》书中有给出两个值的具体取值。下面给出工程上的应用方法：

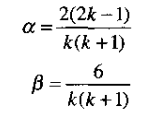
　　如上，可以通过k，即采样时刻来确定两个的值，对于α来说，从k=1开始，而β从k=2开始，滤波从k=3开始。可以看到他们的关系如下图，对于一些应用可以让两者小到一定程度不在改变。

五、线性滤波与非线性滤波

5.1  扩展卡尔曼滤波（EKF）　

　　如上都是讲的是线性模型，即状态方程和量测方程都是线性方程的情况。而实际上，有些传感器得到的是非线性模型，即观测数据与目标动态参数的关系是非线性的。对于非线性滤波，本文简单的介绍一下扩展卡尔曼滤波（EKF）。

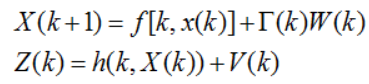
　　对于非线性滤波，至今未得到完善的解法，通常的处理方法是利用线性化技巧将非线性滤波问题转化为一个近似的线性滤波问题，套用线性滤波理论得到求解原非线性滤波问题的次优滤波算法，其中最常用的线性化方法是泰勒级数展开，得到的滤波方法即为扩展卡尔曼滤波。对于二阶EKF，其滤波性能远比一阶的要好，但是二阶以上的效果提升就不明显了，所以一般就是用一阶、二阶，但是二阶计算量比较大，一般都用一阶的。

5.2  泰勒展开

　　泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。

　　

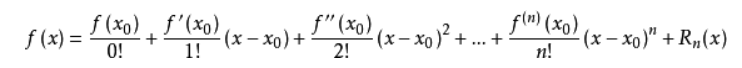
 　　函数的麦克劳林展开指上面泰勒公式中x0取0的情况，即是泰勒公式的特殊形式，若f(x)在x=0处n阶连续可导，则下式成立：

 

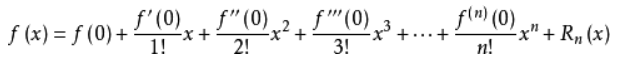
 六、Kalman与最小二乘

6.1  线性回归（LinearRegression）

　　在机器学习中，回归算法是一种有监督的算法，用来建立变量和量测值之间的关系。回归算法的最终结果是一个连续的数据值。既然讲到了Kalman，此处也顺便简单讲解一下这种线性回归问题。

　　线性回归的一个例子：租房价格问题

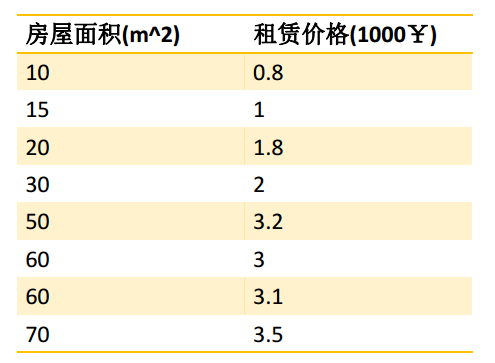
　　对于线性回归，通常构造y = θx + ε 的模型，如果有多个特征，y = θ₁x + θ₂x + ... +ε ，即：

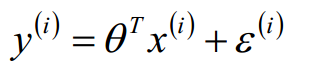
　　参考：线性回归的基本假设

　　然后可以通过最大似然估计，获得损失函数，损失函数的求解，可以通过最小二乘法和梯度下降的方法求解。

　　参考：https://www.cnblogs.com/pinking/p/8722342.html

 　   案例：https://www.cnblogs.com/pinking/p/8970983.html

 　　因此，线性回归是一类问题的概念，而最小二乘估计、最小均方误差估计是参数估计方法，最小二乘法和Kalman都是参数优化方法，包括梯度下降之类的。对于解决类似上面房价预测问题，可以通过最大似然估计进行参数估计，然后根据似然函数构造损失函数，在通过最小二乘法、梯度下降之类的进行求解；当然参数估计也可以利用最小二乘估计，然后通过最小二乘法或梯度下降求具体参数。对于雷达航迹问题，也可以利用最小二乘法求解，当然也可以利用kalman滤波，这是因为我们对于系统模型比较了解。

6.2  Kalman与最小二乘法

 　　最小二乘（Least Square）是优化方法中的一种特殊情况，而卡尔曼滤波又是最小二乘法的一种特殊情况。 古典最小二乘中，假设了每一次测量的权重相同，但事实上这样并不合理，后来演化为加权最小二乘法，至此最小二乘估计所做的都是批处理（Batch），这样比较占内存，不符合动态系统状态估计的需要，即每一次更新输入时，都要从新计算之前所有的记录值。而后，提出递推最小二乘法，模型就不用每次都重新计算了。与递归最小二乘相似，卡尔曼滤波加入了系统内部变化的考虑。即利用process model对系统在下一时刻的状态进行预测。 

　　当对于系统不够了解时，使用最小二乘法比较合适，而对于系统了解比较多时，可以采用Kalman滤波。改变量测噪声、系统噪声都会对Kalman滤波的效果产生影响，而不会对最小二乘滤波产生影响，而改变最小二乘的阶数会对其产生影响。