一、线性回归的基本假设是什么?
使用线性回归模型的四个基本假设:
(1)自变量和因变量满足线性可加
a. 因变量的预测值和自变量满足直线方程,方程中,其余变量当作常量
b. 直线的斜率和其他变量无关
c. 不同因变量的值对于自变量的预测值是可加的
(2)误差是统计独立的
(3)对于任意自变量,误差的方差不变
(4)误差满足正态分布
二、什么是准确率、精确率、召回率
精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。
召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。
准确率(accuracy) = 预测对的/所有
如果我们希望:被检索到的内容越多越好,这是追求“查全率”,即A/(A+C),越大越好。
如果我们希望:检索到的文档中,真正想要的、也就是相关的越多越好,不相关的越少越好,
这是追求“准确率”,即A/(A+B),越大越好。
三、决策树的损失函数以及剪枝系数
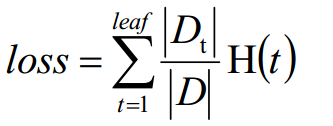
H(t)表示第t个叶子节点的不确定度(信息增益、信息增益率、基尼系数等)
D(t)表示第t个叶子节点的样本数
D表示总共的样本数
通常,节点越多,决策树越复杂,损失也越大。可以对损失函数添加损失系数,修正后的损失函数为:
![]()
对于根节点r的决策树和节点有R个的决策树,剪枝系数表示为:
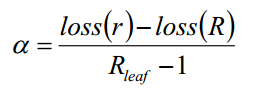
四、简述剪枝操作
前向剪枝:构建决策树的时候,提前停止。
后置剪枝:决策树构建好之后,再进行剪枝,(1)用单一叶子节点代替整个子树(2)将一颗子树完全替代另一颗
对于后置剪枝的过程为:
(1)计算所有内部非叶子节点的剪枝系数
(2)删除最小剪枝系数的节点,若存在多个最小剪枝系数节点,删除包含数据项最多的节点
(3)重复上述过程,直到产生的剪枝决策树只有一个节点
(4)每次删除节点得到决策树Ti
(5)使用验证样本集选择最优子树(即可以通过损失函数验证)
五、决策树的停止条件
方式1:当每个子节点都只有一种类型时停止构建
方式2:节点中的记录数据小于某个阈值且迭代次数达到给定值
方式1容易过拟合、方式2常用
六、分类树和回归树的区别
分类树的叶子节点的预测值一般为概率最大的类别,回归树的叶子节点的预测值一般为所有值的均值,回归树采用均方差作为数的评价指标。
七、交叉熵