一、神经元
神经元模型是一个包含输入，输出与计算功能的模型。（多个输入对应一个输出）
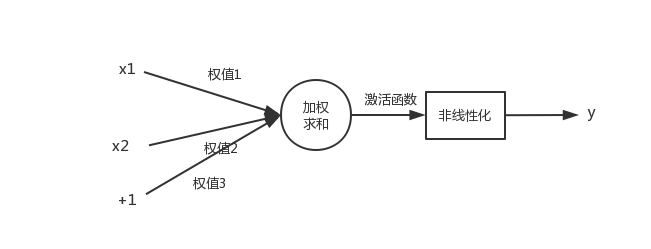
一个神经网络的训练算法就是让权重（通常用w表示）的值调整到最佳，以使得整个网络的预测效果最好。
事实上，在神经网络的每个层次中，除了输出层以外，都会含有这样一个偏置单元。这些节点是默认存在的。它本质上是一个只含有存储功能，且存储值永远为1的单元。
输入：x1、x2和截距+1
输出：y
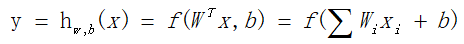
其中的激活函数包括：
逻辑回归函数（S函数）：
双曲正切函数（双S函数）：
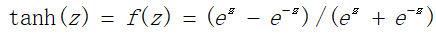
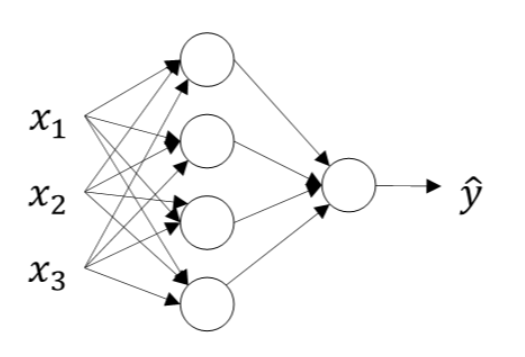
二、神经网络的层次
神经网络中，除了输入层、输出层，其他的都为隐层。
对于隐层较少（2个隐层以下）的神经网络叫做浅层神经网络，也叫做传统神经网络。增加隐层的话，就成为了深层神经网络（DNN）。
|
单隐层神经网络（浅层） |
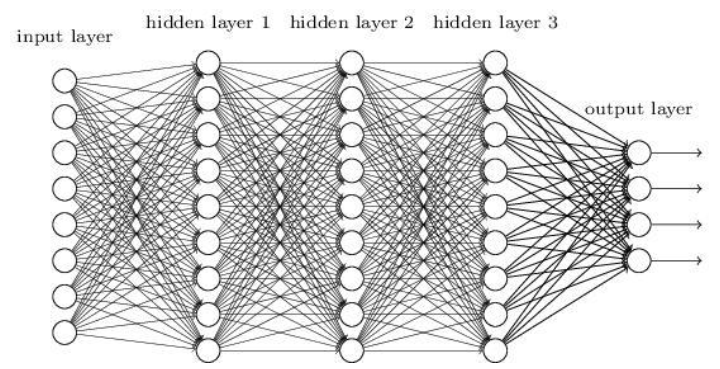
深层神经网络 |
1989年Robert Hecht-Nielsen证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的神经网络来逼近，这就是万能逼近定理。所以一个三层的神经网络就可以完成任意的m维到n维的映射。即这三层分别是输入层（I）、隐含层（H）、输出层（O）。
神经网络中，输入层和输出层的节点个数都是确定的，而隐含层节点个数不确定，可以通过经验公式来得到：
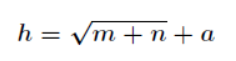
m、n分别代表输入节点个数和输出节点个数。a是一个取值从1~10之间的调节常数。
三、网络表达力与过拟合
 |
 |
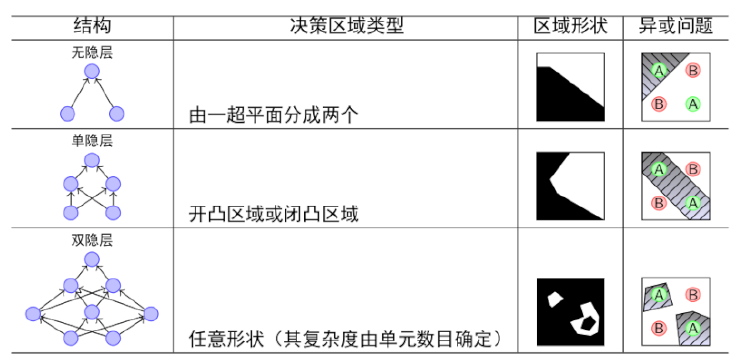
1.单隐层神经网络可以逼近任何连续函数。连续函数你可以看成是一条不断的线，可以是一条任何弯曲的线，线的两侧是被区分的两个类别。之所以说可以是任一的线，是因为再怎么扭曲的线都是可以用无限小的直线连接而成，既然是直线，那就可以使用线性分类器，所以，一条曲线就可以用许多线性分类器组成，当同时满足线性分类器都为1时，那么整个曲线的神经网就被满足为1了。其实这个就是上文我们详述的“逻辑与”，而“逻辑与”我们只需要使用“单层神经网”。如果在这个隐层中的神经元的个数越多，就越逼近。（一个神经元就是一个线性分类器，分类器越多，就越你和曲线），另外的解释可以看第五单元。
2.多隐藏层比单隐藏层效果好。举个例子，我们使用单隐层，里面有1000个神经元，和我们使用一个多隐层，里面有50个神经元，也许达到的效果差不多，但是工业上我们仍然选择后者会有更好的效率。
3.对于分类，3层神经网（1个隐层）比2层神经网（无隐层）的效果好，因为前者可以区分非线性。但是！层数再往上增多，则效果的上升就不那么明显了。所以考虑“使用最简单的模型达到最好的效果”这个原则，我们更愿意选择3层神经网。
4.图像处理之所以需要深层次的神经网，是因为将图像转换成结构化的数据需要有非常多的维度，也就是说需要非常多的特征才能来描述图片。
粘贴自：http://blog.csdn.net/sinat_33761963/article/details/52219677
四、BP算法
BP神经网络属于传统神经网络，是一种求解权重w的算法。通常分为两部：
（1）FP：信号正向传递（FP）求损失
（2）BP：损失反向回传（BP）
算法推到过程：
（1）正向传递求损失，这个过程较为简单，即对于输入x、偏置1与权值w和b进行各个层次的加权、并通过激活函数的计算，求出输出的值。
如上假设最终求出的值分别为d1、d2，则输出层误差的表达式为：
（2）所谓的反向传输过程：
---------------------随机梯度下降法----------------
当误差求出来之后，采用随机梯度下降的方法（SGD），每看一个数据就算一下损失函数，然后求梯度更新参数，这个称为随机梯度下降。
即对于误差E求他的梯度，即误差下降最快的方向，然后根据这个值修正权值，即当权值为这个修正值时，求的误差会比当前的误差小的最大。
例子：
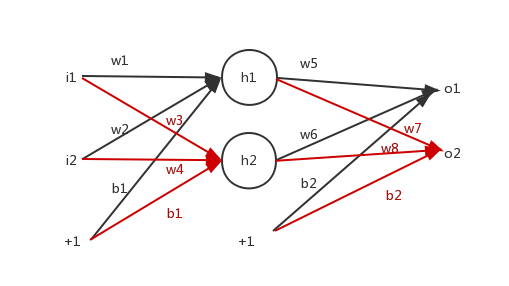
正向求误差：
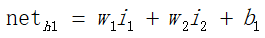
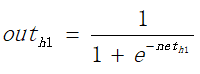
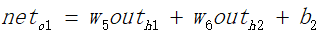
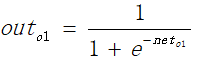
同理可以求获得的o2的值。
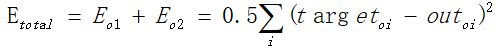
如上，可以求得正向误差。
反向损失回传：
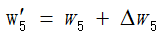
如上，想要修正权值，这个
需要通过随机梯度下降法求得，即对误差求梯度，让这个误差下降最大方向的值作为修正误差。
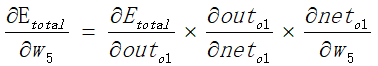
当然这个过程就比较麻烦了计算起来。此处不做详细推倒。
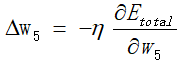
这样就可以修正权值了。
对于例子中，对上一层的权值进行修正的过程基本和上面相似，不过不同的地方就是梯度的求解，需要多考虑一层偏导的计算。
通常，BP算法一般迭代1000次，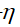
的取值为0.5。
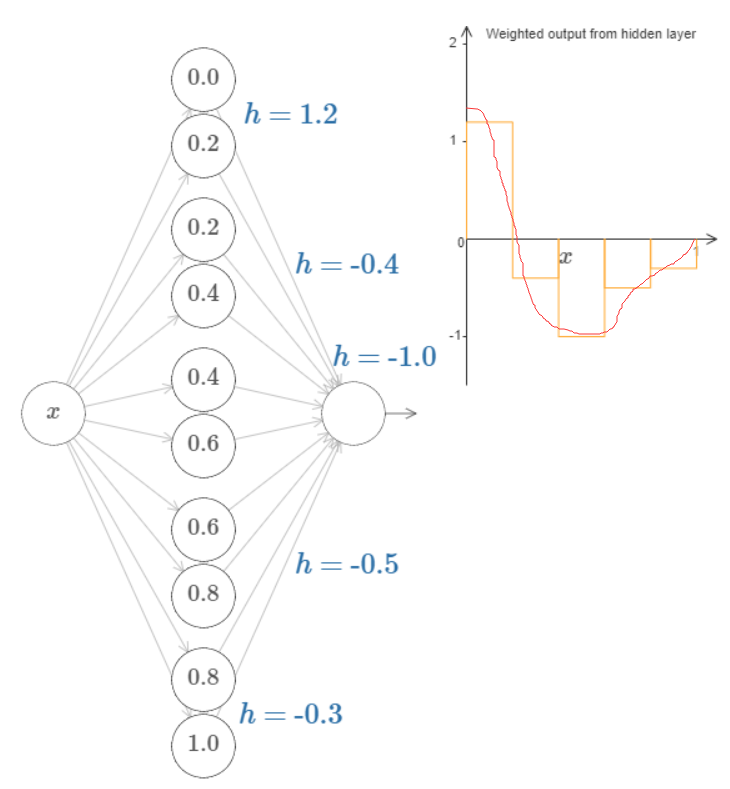
五、对于单隐层可以拟合任意函数的理解
单隐层神经网络可以逼近任何连续函数。对于这个的解释，可以参考：http://neuralnetworksanddeeplearning.com/chap4.html
当然，两个重要的前提：逼近和任意连续函数。不过对于连续函数这个限制并不是严格的，因为如果目标函数是一个离散的，通常可以用连续函数来逼近。“However, even if the function we'd really like to compute is discontinuous, it's often the case that a continuous approximation is good enough. If that's so, then we can use a neural network. In practice, this is not usually an important limitation.”
对于上面文章的解释，我觉得总结起来就是：
激活函数sigmoid（wx+b）可以看作是一个阶跃函数，如果存在两个激活函数就可以构造一个"bump" function；
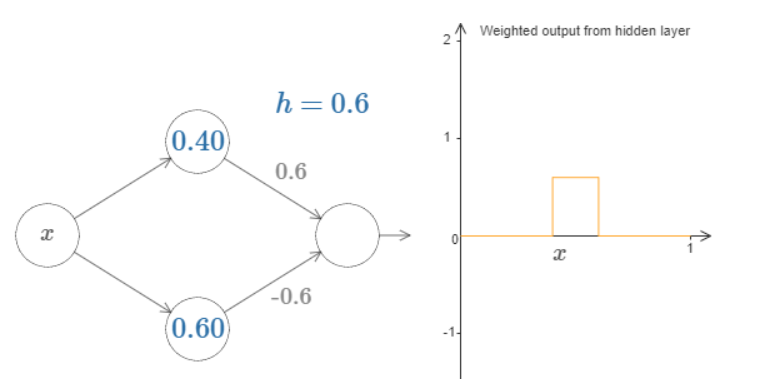
当然你的神经元多了，就可以拟合任意函数了：
