此博客链接:
三数之和的多种可能
题目链接:https://leetcode-cn.com/problems/3sum-with-multiplicity/
题目
给定一个整数数组 A,以及一个整数 target 作为目标值,返回满足 i < j < k 且 A[i] + A[j] + A[k] == target 的元组 i, j, k 的数量。
由于结果会非常大,请返回 结果除以 10^9 + 7 的余数。
示例 1:
输入:A = [1,1,2,2,3,3,4,4,5,5], target = 8
输出:20
解释:
按值枚举(A[i],A[j],A[k]):
(1, 2, 5) 出现 8 次;
(1, 3, 4) 出现 8 次;
(2, 2, 4) 出现 2 次;
(2, 3, 3) 出现 2 次。
示例 2:
输入:A = [1,1,2,2,2,2], target = 5
输出:12
解释:
A[i] = 1,A[j] = A[k] = 2 出现 12 次:
我们从 [1,1] 中选择一个 1,有 2 种情况,
从 [2,2,2,2] 中选出两个 2,有 6 种情况。
题解
使用双指针的想法,定义一个left和一个right,从数组两头遍历数组,判断加上中间数字的和是否等于目标数字。如果三数之和小于目标值,则把left加一,如果三数只和大于目标值,则把right减一,直到找到 。
一顿操作后,我发现示例2就过不去,才发现自己想错了,真是把力扣中的中等题不当回事了。这题怎么看都需要排列组合,先回忆一波排列组合。
排列组合
定义:从n个数中取出m个数,有多少种取法就叫做排列组合。
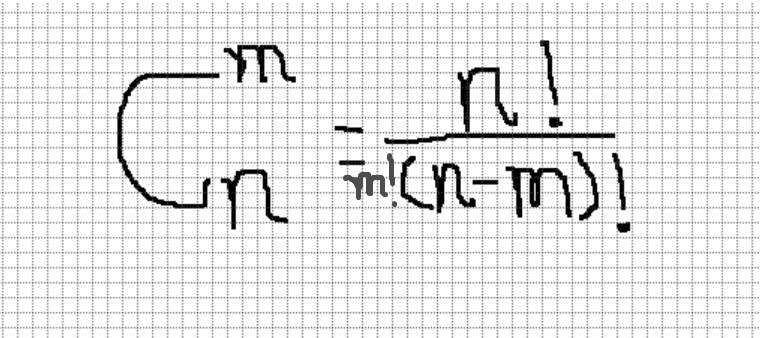
正确思路:
把给的数组进行处理,以给的数为新数组res的下标,累加每个数的个数。这题找三个数之和的可能性,这三个数分为三种情况。
情况1:三个数相等,找出arr中大于3的数,并且求其中3的组合。
情况2:三个数只有两个数相等,另外一个数不相等,找出arr中大于2的数,并且求出2的组合。
情况3:三个数都不相等,找出arr中等于1的数,并且和为目标数的三个数。
代码
class Solution { public int threeSumMulti(int[] arr, int target) { int left=0; int right=arr.length-1; int res[]=new int [100]; int count=0; for(int i=0;i<arr.length;i++) { res[arr[i]]++; } // Arrays.sort(res); //情况1:三个数一样 if(target%3==0) { for(int i=0;i<=100;i++) { if(3*i==target&&arr[i]>=3) { count+=zuhe(res[i],3); } } } for(int i=0;i<=100;i++) { if(2*i>target) { break; } for(int j=i+1;j<=100;j++) { if(2*i+j==target&&res[i]>=2) { System.out.print(i); System.out.print(j); count+=zuhe(res[i],2)*res[j]; System.out.print(count); } if(i+2*j==target&&res[j]>=2) { System.out.print(i); System.out.print(j); count+=zuhe(res[j],2)*res[i]; System.out.print(count); } } } for(int i=0;i<=100;i++) { if(i>target) { break; } for(int j=i+1;j<=100;j++) { for(int k=j+1;k<=100;k++) { if(i+j+k==target) { count+=res[i]*res[j]*res[k]; } } } } return count; } public int zuhe(int n,int m){ int up=1; int down=1; for(int i=n;i>=n-m;i--){ up*=i; } for(int j=2;j<=m;j++) { down*=j; } return up/down; } }