Matlab中的eig函数和Opecv中eigen（）函数的区别

奇异值分解的理论参见下面的链接

http://www.cnblogs.com/pinard/p/6251584.html

 https://blog.csdn.net/shenziheng1/article/details/52916278

 https://blog.csdn.net/billbliss/article/details/78579308

 https://blog.csdn.net/zhongkejingwang/article/details/43053513

https://blog.csdn.net/u010099080/article/details/68060274

在Matlab中的eig()函数，和Opencv中的eigen()函数，都是用来获得矩阵的特征值和特征矢量。并且，这两个函数的输入矩阵必须是对称矩阵。

Matlab中的eig()函数，常见的写法如下：

[V D]=eig(A);

D是矩阵A的特征值组成的对角矩阵，与A是同数据类型，同尺度。V是与特征值对应的特征矢量组成的矩阵。

在Opencv中的eigen()函数，常见的写法如下：

myEigen(A,D,V);
函数中的A是输入矩阵，D和V是输出的特征值矢量和特征矢量组成的矩阵。eig()函数与eigen()函数的不同之处是：

1、在eigen()中的D是一个一维特征值组成的列矢量，并且特征值是按照降序排序；而在eig()中的D则是一个以特征值为对角的对角矩阵，特征值是按照升序排序。

   2、在eigen()中的V是特征矢量组成的矩阵，矩阵中的每一行就是一个特征矢量；而在eig()中的V则是以特征矢量组成的矩阵，矩阵中的每一列即是一个特征矢量。

下面是同一个实例，在Matlab中和Opencv中的比较：

首先是Matlab中的eig函数的实例代码：

clear;
clc;
A=[1,2,3;
     2,5,6;
     3,6,9];
 [V D]=eig(A);
 A_r=V*D*V';

输入结果如下：

   

下面是Opencv中eigen函数的实例代码：

//为方便与Matlab中的eig（）函数比较，我把eigen封装在一个函数里，并将特征值矢量转换成对角矩阵，与Matlab中类似
void myEigen(Mat&A,Mat&D,Mat&V)
{
    eigen(A,D,V);
    Mat E=Mat::eye(A.size(),A.type());
    for(int i=0;i<A.rows;i++)
    {
        E.at<double>(i,i)=D.at<double>(0,i);
    }
    D=E.clone();

}
const double eps=2.224e-16;
int main()
{
    Mat A=(Mat_<double>(3,3)<<
           1,2,3,
           2,5,6,
           3,6,9);
    Mat D,V;
    myEigen(A,D,V);

    Mat A_r=V.t()*D*V;

    cout<<"原矩阵  A  ="<<endl<<A<<endl;
    cout<<"重构矩阵A_r="<<endl<<A_r<<endl<<endl;
    cout<<"D="<<endl<<D<<endl;
    cout<<"V="<<endl<<V<<endl;
    return 0;
}

输出结果如下：

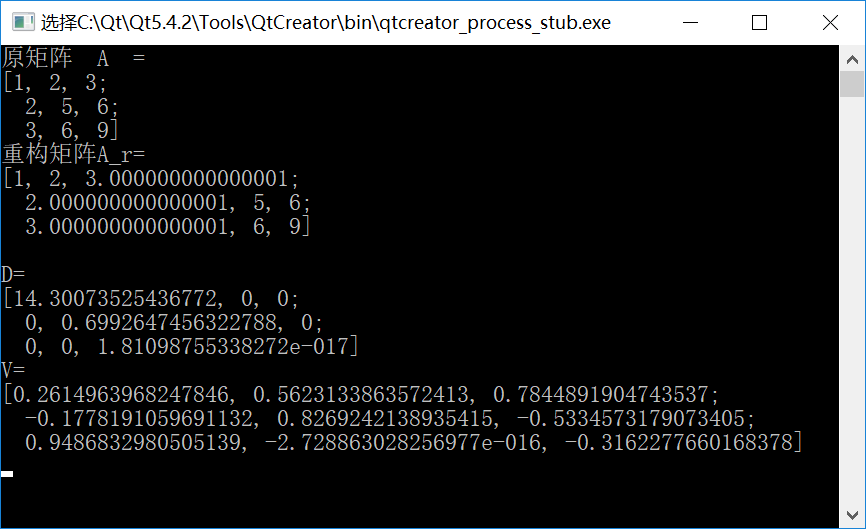
比较Matlab和Opencv中的D、V值：

  

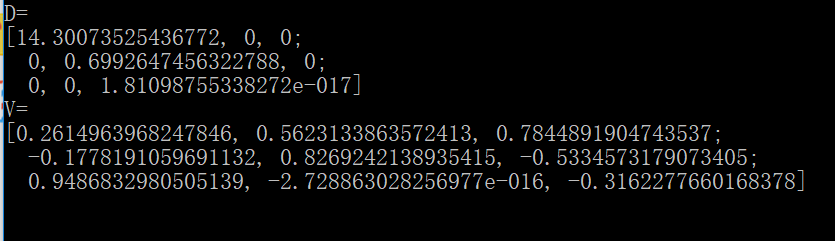
Opencv中V的第一列，与Matlab中V的第一行数值一直，但排序相反，其它行列对比也基本一致。