Link
https://jzoj.net/senior/#main/show/3777
Description
小Y最近学得了最短路算法,一直想找个机会好好练习一下。话虽这么说,OJ上最短路的题目都被他刷光了。正巧他的好朋友小A正在研究一类奇怪的图,他也想凑上去求下它的最短路。
小A研究的图可以这么看:在一个二维平面上有任意点(x,y)(0<=x<=N,0<=y<=M,且x,y均为整数),且(x,y)向(x-1,y)(必须满足1<=x)和(x,y-1)(必须满足1<=y)连一条边权为0的双向边。
每个点都有一个非负点权,不妨设(x,y)的权值为F[x][y],则有:
1.x=0或y=0:F[x][y]=1;2.其他情况:F[x][y]=F[x-1][y]+F[x][y-1]。
现在,小Y想知道(0,0)到(N,M)的最短路,即使得经过的点的权值之和最小。为了炫耀自己学过最短路算法,他决定和你进行一场比赛,看谁的程序跑得快。然则小Y没有学过高精度算法,所以他希望输出答案时只输出答案模1000000007后的值。
Solution
题目大意
求从(0,0)~(n,m)经过点的和的最小值。
第(x,y)点的权值为f[x,y],他的计算方法是f[x,y]=f[x-1,y]+f[x,y-1],如果(x=0) or (y=0)那么f[x,y]的值为1
60分
很显然,可以直接暴力枚举,求出答案。
100分
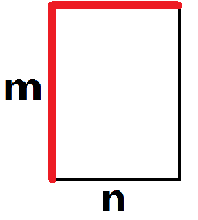
通过一系列的对拍,我们可以发现,如下图红边的走法,必定最优,但不知道怎么证明。我们设较短边的长为n,较长边的长为m
我们可以总结成一个公式
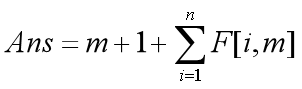
那么,关键就成了如何求出F[i,m] (i=1~n)。
我们考虑把他转化成组合数的形式
根据题目给出的F数组计算方法,可以得出f[x,y]=C(min(x,y),x+y)
那么显然F[i,m] (i=1~n)就是C(i,i+m) (i=1~n)
其实每个组合数,可以理解成一个数除另一个数,比如对于C(n,m)
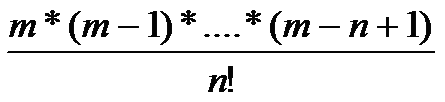
试想一下,如果x<y,求C(x,y)+C(x+1,y+1)+C(x+2,y+2),我们设上面这个式子分子为tot1,分母为tot2
C(x+1,y+1)相比C(x,y)的tot1和tot2,发现tot1多乘了y+1,tot2多乘了x+1,
C(x+2,y+2)相比C(x+1,y+1)的tot1和tot2,发现tot1多乘了y+2,tot2多乘了x+2
说明,我们每次循环,tot1都乘i+m,tot2都乘i,那么,每次的C(i,i+m)就是tot1/tot2
但是问题来了,tot1和tot2都很大,如果相除是不太可能的,先mod再除答案是错误的,只能使用逆元了。
逆元
根据费马小定理可以得到如下式子
![]()
两边同时除b得到,高斯研究过,发现是等价的
![]()
两边同时除b得到,高斯研究过,发现是等价的

两边同时乘一个a,并且交换位置,得到如下式子
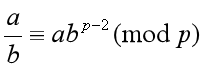
发现,我们要求a除b取模p的结果,其实是等价于abp-2取模p的结果的,也就是说,欲想知道a除b取模p的结果,其实就是算出abp-2取模p的结果就行了
因为a*b mod p,是等价于a mod p*b mod p的,ak mod p是等价于(a mod p)k的,所以我们这里可以取mod来避免高精度。
当然,F[i,m] (i=1~n)这一部分,可以使用一个组合公式就可以了,具体实现和题解请选手自行考虑。