凡人用迭代,神仙用递归。
今天学习了熟悉而又陌生的递归,写个博客总结一下。
以我的个人理解,递归就是函数直接或间接地调用自己,在形态上就是数学函数的直观体现。即如果给了一个问题,你可以用数学函数进行描述,那递归算法就基本上出来了。
虽然在直观上不好理解(也可能是我的思维习惯了迭代,不习惯递归),但是反应在代码上属实简洁。
那么什么问题适合用递归算法呢?那估计就是套娃的问题吧,如果一个问题每一步的解决方案都是类似的,那多半是适用于递归的。
以一个实例来运用一下递归算法。
将x轴上的圆饼,挪到z轴上,移动过程中,每次只能移动一个圆饼,且须保证大饼在下,小饼在上,最后将移动顺序输出
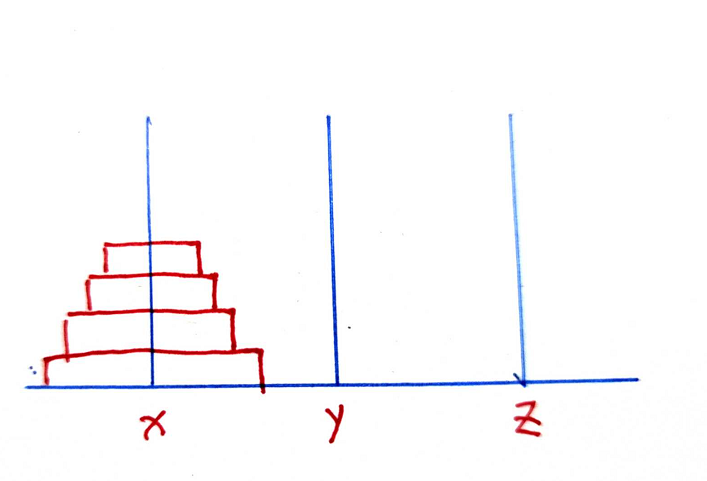
分析:要实现的目的,将X轴上4个圆饼悉数挪到Z轴
前一步:将三个圆饼,从X,借助Z轴中介,挪到Y轴;将X轴最后一个圆饼挪到Z轴;将Y轴上的三个圆饼,借助X轴做中介,挪到Z轴;
那么如何将三个圆饼,从X,挪到Y轴?
将两个圆饼,从X,借助Y,挪到Z轴;将第三个圆饼,从X挪到Y;将Z轴上的两个圆饼,借助X,挪到Y;
我们发现:每一步要解决的问题,都被分解为了相似的三小步。
写成递归算法,便如下所示。
1 #include <iostream>
2
3 using namespace std;
4
5 //将n个盘子从X轴上,借助Y,移动到Z轴上
6 void move(int n, char x, char y, char z)
7 {
8 if (n == 1)
9 cout << x << "-->" << z << endl;
10 else
11 {
12 move(n - 1, x, z, y);
13 cout << x << "-->" << z << endl;
14 move(n - 1, y, x, z);
15 }
16 }
17
18 int main()
19 {
20 int n;
21 cout << "请输入汉诺塔层数:" << endl;
22 cin >> n;
23 cout << "执行步骤为:" << endl;
24 move(n, 'X', 'Y', 'Z');
25
26 int u;
27 cin >> u;
28 }
感想:真的超难理解,欠缺递归思维。