题目描述:
猫和老鼠在10*10的方格中运动,例如:
*...*.....
......*...
...*...*..
..........
...*.C....
*.....*...
...*......
..M......*
...*.*....
.*.*......
C = 猫(CAT) M = 老鼠(MOUSE) * = 障碍物 . = 空地
猫和老鼠每秒中走一格,如果在某一秒末他们在同一格中,我们称他们“相遇”。
注意,“对穿”是不算相遇的。猫和老鼠的移动方式相同:平时沿直线走,下一步如果会走到障碍物上去或者出界,就用1秒的时间做一个右转90度。一开始他们都面向北方。 编程计算多少秒以后他们相遇。
输入文件
10行,格式如上。
输出文件
相遇时间T。如果无解,输出-1。
样例输入
*...*.....
......*...
...*...*..
..........
...*.C....
*.....*...
...*......
..M......*
...*.*....
.*.*......
样例输出
49
题解
正解应该就是暴力模拟吧……对于普通解法就直接贴代码吧。
#include <cstdlib>
#include <cstdio>
#include <iostream>
using namespace std;
const int maxn = 10;
int mx, my;
int cx, cy;
int cd, md;
char mmap[maxn][maxn];
int dirx[] = {-1, 0, 1, 0};
int diry[] = {0, 1, 0, -1};
int main()
{
freopen("catch.in", "r", stdin);
freopen("catch.out", "w", stdout);
for(int i = 1; i <= 10; ++i)
{
gets(mmap[i]+1);
for(int j = 1; j <= 10; ++j)
{
if(mmap[i][j] == 'C')
{
cx = i;
cy = j;
}
else if(mmap[i][j] == 'M')
{
mx = i;
my = j;
}
}
}
cd = md = 0;
for(int bs = 1; bs <= 10000; ++bs)//如果步数大于10000就跳掉,这里不能保证正确性
{
int tx = mx + dirx[md];
int ty = my + diry[md];
if(mmap[tx][ty] == '*' || !tx || tx > 10 || !ty || ty > 10)
md = (md+1) % 4;//右转
else
{
mx = tx;
my = ty;
}
tx = cx + dirx[cd];
ty = cy + diry[cd];
if(mmap[tx][ty] == '*' || !tx || tx > 10 || !ty || ty > 10)
cd = (cd+1) % 4;
else
{
cx = tx;
cy = ty;
}
if(mx == cx && my == cy)
{
printf("%d", bs);
return 0;
}
}
puts("-1");
return 0;
}
是否感觉bs <= 10000太草率了?于是我们可以考虑找到环后直接用exgcd解方程。
一下用的均是mj大佬的代码
所以首先是漫长的找环过程,vis数组要记录横纵坐标及方向。
nowc=0;
nowm=0;
f[cx][cy][0]=g[mx][my][0]=t=1;
while(1)
{
int nx=cx+d[nowc][0],ny=cy+d[nowc][1];
if(s[nx][ny]!='*')
{
cx=nx;
cy=ny;
}
else nowc=(nowc+1)%4;
if(!f[cx][cy][nowc]) f[cx][cy][nowc]=++t;
else break;
}
tc=t+1;
t=1;
while(1)
{
int nx=mx+d[nowm][0],ny=my+d[nowm][1];
if(s[nx][ny]!='*')
{
mx=nx;
my=ny;
}
else nowm=(nowm+1)%4;
if(!g[mx][my][nowm]) g[mx][my][nowm]=++t;
else break;
}
我们要分成这样几种情况:
如图,红色为鼠的路线,绿色为猫的路线。
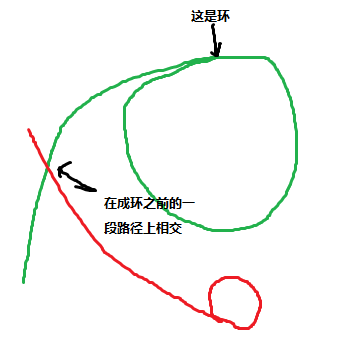
这种情况最好办,直接判一下相等即可。
if(f[i][j][k]<f[cx][cy][nowc]&&g[i][j][l]<g[mx][my][nowm])
{
if(f[i][j][k]==g[i][j][l]) ans=min(ans,f[i][j][k]-1);
continue;
}
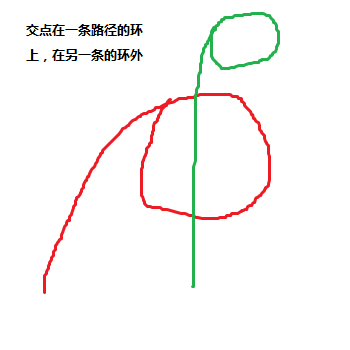
由于是在绕圈,我们可以很容易地想到取模,于是我们大力算出两个交点的时间去min即可。
if(f[i][j][k]<f[cx][cy][nowc])
{
if((f[i][j][k]-g[i][j][l])%(tm-g[mx][my][nowm])==0) ans=min(ans,f[i][j][k]-1);
continue;
}
if(g[i][j][l]<g[mx][my][nowm])
{
if((g[i][j][l]-f[i][j][k])%(tc-f[cx][cy][nowc])==0) ans=min(ans,g[i][j][l]-1);
continue;
}
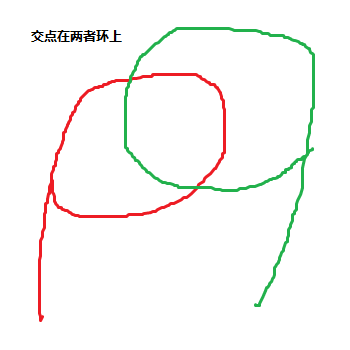
我们以求点a的时间为例:
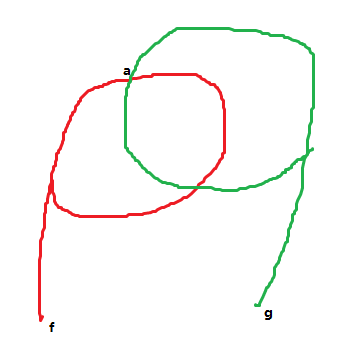
我们设(f o a)的时间为(a),(t o a)的时间为(b),红色环的大小为(k_f),绿色环大小为(k_t),红色绕了(x)圈,绿色绕了(y)圈。我们有:(k_f x + a = k_t y +b)。发现是一个exgcd模板。
感觉这跟poj1061 青蛙的约会差不多。
注意先用裴蜀定理判一下无解情况。
int tmx=tc-f[cx][cy][nowc],tmy=tm-g[mx][my][nowm];
int gd=gcd(tmx,tmy),ch,x,y;
if(g[i][j][l]>f[i][j][k])
{
if((g[i][j][l]-f[i][j][k])%gd!=0) continue;
ch=(g[i][j][l]-f[i][j][k])/gd;
}
else
{
if((f[i][j][k]-g[i][j][l])%gd!=0) continue;
ch=(f[i][j][k]-g[i][j][l])/gd;
}
exgcd(tmx,tmy,x,y);
ans=min(ans,x*ch*tmx+f[i][j][k]-1);
那下面就放一下完整代码吧。
#include <map>
#include <set>
#include <queue>
#include <cmath>
#include <vector>
#include <cstdio>
#include <bitset>
#include <cstring>
#include <iostream>
#include <algorithm>
#define inf 0x3f3f3f3f
// #define maxn
// #define int long long
using namespace std;
void write(int x){if(x<0){putchar('-');x=-x;}if(x>9) write(x/10);putchar(x%10+'0');}
int read(){int d=0,w=1;char c=getchar();for(;c<'0'||c>'9';c=getchar())if(c==
'-')w=-1;for(;c>='0'&&c<='9';c=getchar())d=(d<<1)+(d<<3)+c-48;return d*w;}
void wln(int x){write(x);putchar('
');}
void wrs(int x){write(x);putchar(' ');}
int d[4][2]={{-1,0},{0,1},{1,0},{0,-1}},cx,cy,mx,my,tc,tm,f[12][12][5],g[12][12][5],nowm,nowc,t,ans;
char s[12][12];
int gcd(int x,int y)
{
return y?gcd(y,x%y):x;
}
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,y,x);
y-=a/b*x;
return;
}
signed main()
{
// freopen("catch.in","r",stdin);
// freopen("catch.out","w",stdout);
for(int i=1;i<11;i++)
gets(s[i]+1);
for(int i=1;i<11;i++)
s[i][0]=s[i][11]=s[0][i]=s[11][i]='*';
for(int i=1;i<11;i++)
for(int j=1;j<11;j++)
{
if(s[i][j]=='C')
{
cx=i;
cy=j;
}
if(s[i][j]=='F')
{
mx=i;
my=j;
}
}
nowc=0;
nowm=0;
/*以下找环*/
f[cx][cy][0]=g[mx][my][0]=t=1;
while(1)
{
int nx=cx+d[nowc][0],ny=cy+d[nowc][1];
if(s[nx][ny]!='*')
{
cx=nx;
cy=ny;
}
else nowc=(nowc+1)%4;
if(!f[cx][cy][nowc]) f[cx][cy][nowc]=++t;
else break;
}
tc=t+1;
t=1;
while(1)
{
int nx=mx+d[nowm][0],ny=my+d[nowm][1];
if(s[nx][ny]!='*')
{
mx=nx;
my=ny;
}
else nowm=(nowm+1)%4;
if(!g[mx][my][nowm]) g[mx][my][nowm]=++t;
else break;
}
tm=t+1;
ans=inf;
/*寻找最少情况*/
for(int i=1;i<11;i++)
for(int j=1;j<11;j++)
for(int k=0;k<4;k++)
for(int l=0;l<4;l++)
if(f[i][j][k]&&g[i][j][l])
{
/*情况1*/
if(f[i][j][k]<=f[cx][cy][nowc]&&g[i][j][l]<=g[mx][my][nowm])
{
if(f[i][j][k]==g[i][j][l]) ans=min(ans,f[i][j][k]-1);
continue;
}
/*情况2*/
if(f[i][j][k]<=f[cx][cy][nowc])
{
if(f[i][j][k]>=g[i][j][l]&&(f[i][j][k]-g[i][j][l])%(tm-g[mx][my][nowm])==0) ans=min(ans,f[i][j][k]-1);
continue;
}
if(g[i][j][l]<=g[mx][my][nowm])
{
if(g[i][j][l]>=f[i][j][k]&&(g[i][j][l]-f[i][j][k])%(tc-f[cx][cy][nowc])==0) ans=min(ans,g[i][j][l]-1);
continue;
}
/*情况3,最复杂的情况,然而yj大佬说数据中没有*/
int tmx=tc-f[cx][cy][nowc],tmy=tm-g[mx][my][nowm];
int gd=gcd(tmx,tmy),ch,x,y;
if(g[i][j][l]>f[i][j][k])
{
if((g[i][j][l]-f[i][j][k])%gd!=0) continue;
ch=(g[i][j][l]-f[i][j][k])/gd;
}
else
{
if((f[i][j][k]-g[i][j][l])%gd!=0) continue;
ch=(f[i][j][k]-g[i][j][l])/gd;
}
exgcd(tmx,tmy,x,y);
ans=min(ans,x*ch*tmx+f[i][j][k]-1);
}
write(ans==inf?0:ans);
return 0;
}