目标函数:
$ J = frac{1}{2} left| R - PQ ight|^{2} + lambda left( left|P ight|^{2} +left| Q ight|^{2} ight) $
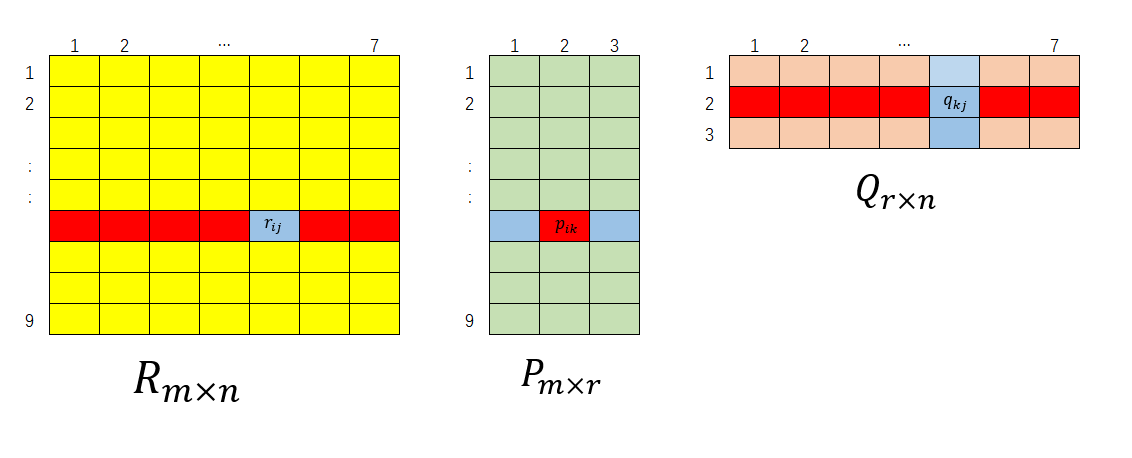
矩阵R为$ m imes n$的稀疏矩阵(sparse matrix),考虑用 $ P_{m imes r}$ 和 $ Q_ {r imes n }$ 两个矩阵的乘积 $ hat{R} $ 去逼近矩阵R,误差用SSE,后面面 两项为 正则项。
1,Gradient Descent
$ J = frac{1}{2}sum _{left(i,j ight) in D} left( r_{ij} - sum_{k=1}^{r} p_{ik} q_{kj} ight)^2 + lambda left ( left | P ight | ^2+ left | Q ight |^2 ight )$
整体误差$ J $对 因子矩 P 中某元素 $ p_{ik} $ 的偏导数:
$frac{partial J}{partial p_{ik}} = sum _{left(i,j ight) in D} left( r_{ij} - sum_{k=1}^{r} p_{ik} q_{kj} ight)q_{kj}+ lambda p_{ik} $
偏导数矩阵应注意的几项:
1 $ sum _{left(i,j ight) in D} left( r_{ij} - sum_{k=1}^{r} p_{ik} q_{kj} ight)q_{kj} $ 中并不是所有项都有定义的,只取有定义位置。
2 对于给定的元素 $ p_{ik} $,i,k都是确定的,$ sum _{left(i,j ight) in D} left( r_{ij} - sum_{k=1}^{r} p_{ik} q_{kj} ight)q_{kj} $所以可以看成$ left ( hat{R} -R ight )$ 和 Q 红色非空部分的内积, 进一步还能得到因子矩阵的梯度矩阵 $ frac{partial J}{partial P} = left ( R-hat{R} ight ) Q^T + lambda P $
也可以直接用矩阵求导的方法来求解:

当然,做乘法时依然只是那些有记录的位置参与计算。