K-means
定义
k-means是一种基于距离的聚类算法。k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。
其处理过程如下:
- 随机选择k个点作为初始的聚类中心;
- 对于剩下的点,根据其与聚类中心的距离,将其归入最近的簇
- 对每个簇,计算所有点的均值作为新的聚类中心
- 重复2、3直到聚类中心不再发生改变

K-means的缺点
-
K-Means forms spherical clusters only. This algorithm fails when data is not spherical ( i.e. same variance in all directions).
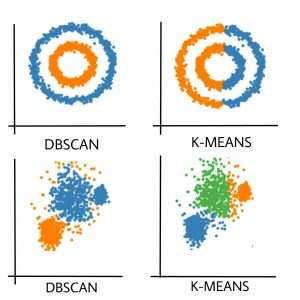
-
K-Means algorithm is sensitive towards outlier. Outliers can skew the clusters in K-Means in very large extent.
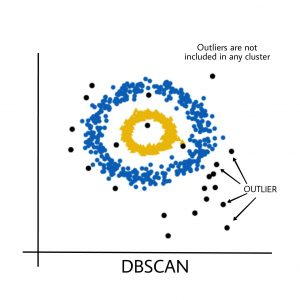
-
K-Means algorithm requires one to specify the number of clusters a priory etc.
Basically, DBSCAN algorithm overcomes all the above-mentioned drawbacks of K-Means algorithm. DBSCAN algorithm identifies the dense region by grouping together data points that are closed to each other based on distance measurement.
DBSCAN
定义
DBSCAN算法是一种基于密度的聚类算法:
- 聚类的时候不需要预先指定簇的个数
- 最终的簇的个数不定
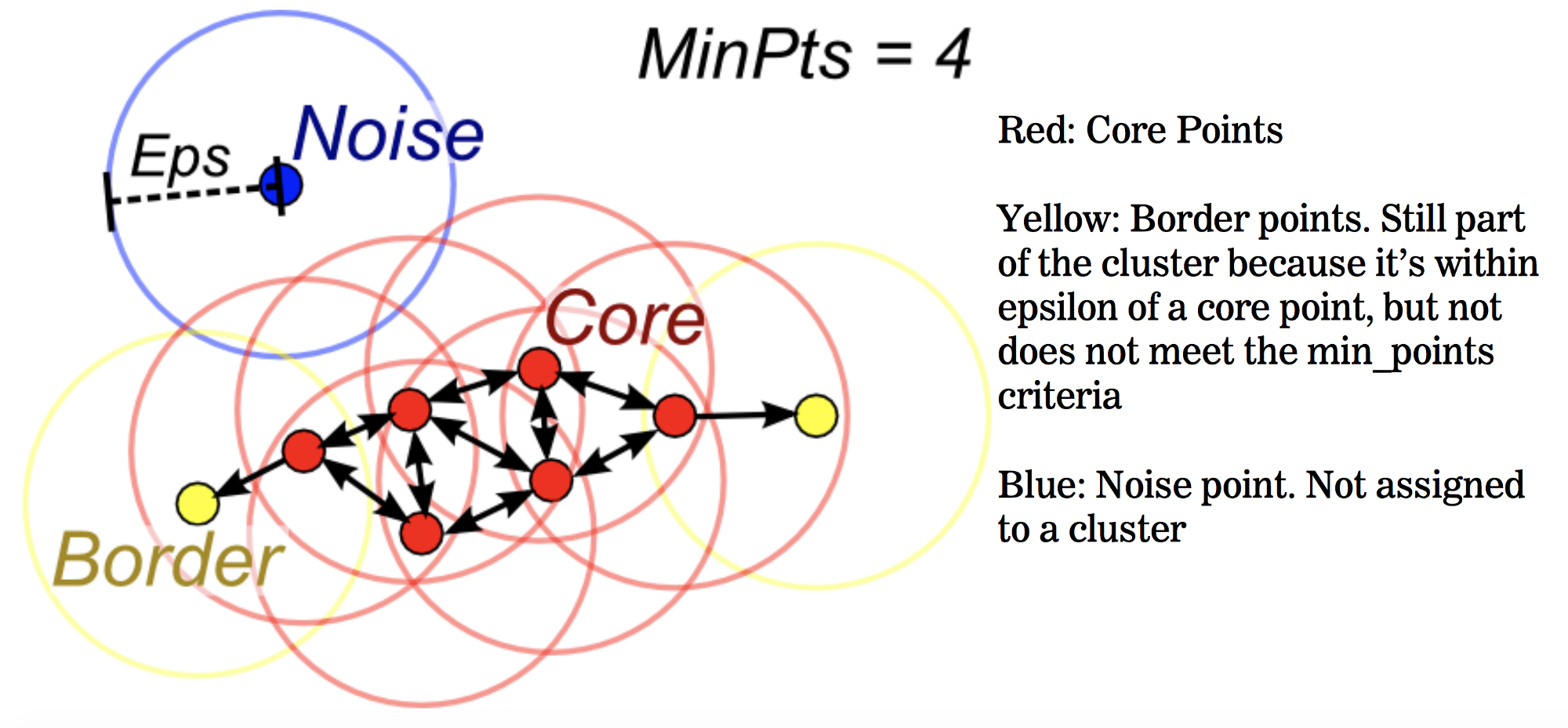
DBSCAN算法将数据点分为三类:
- 核心点:在半径Eps内含有超过MinPts数目的点
- 边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内
- 噪音点:既不是核心点也不是边界点的点
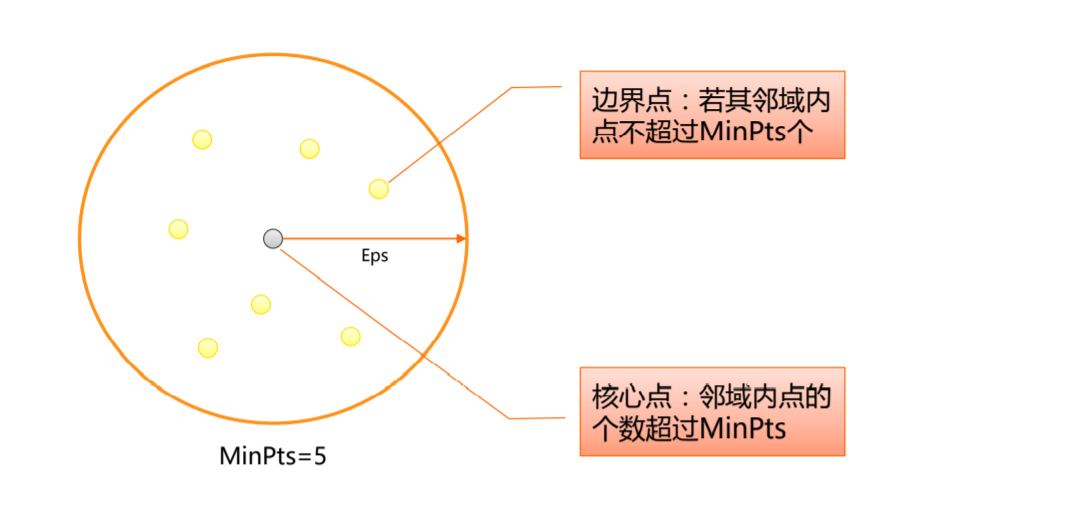
DBSCAN算法流程:
- 将所有点标记为核心点、边界点或噪声点;
- 删除噪声点;
- 为距离在Eps之内的所有核心点之间赋予一条边;
- 每组连通的核心点形成一个簇;
- 将每个边界点指派到一个与之关联的核心点的簇中(哪一个核心点的半径范围之内)。
更严谨的定义
首先定义几个相关的概念:
- 邻域:对于任意样本i和给定距离e,样本i的e邻域是指所有与样本i距离不大于e的样本集合;
- 核心对象:若样本i的e邻域中至少包含MinPts个样本,则i是一个核心对象;
- 密度直达:若样本j在样本i的e邻域中,且i是核心对象,则称样本j由样本i密度直达;
- 密度可达:对于样本i和样本j,如果存在样本序列p1,p2,...,pn,其中p1=i,pn=j,并且pm由pm-1密度直达,则称样本i与样本j密度可达;
- 密度相连:对于样本i和样本j,若存在样本k使得i与j均由k密度可达,则称i与j密度相连。
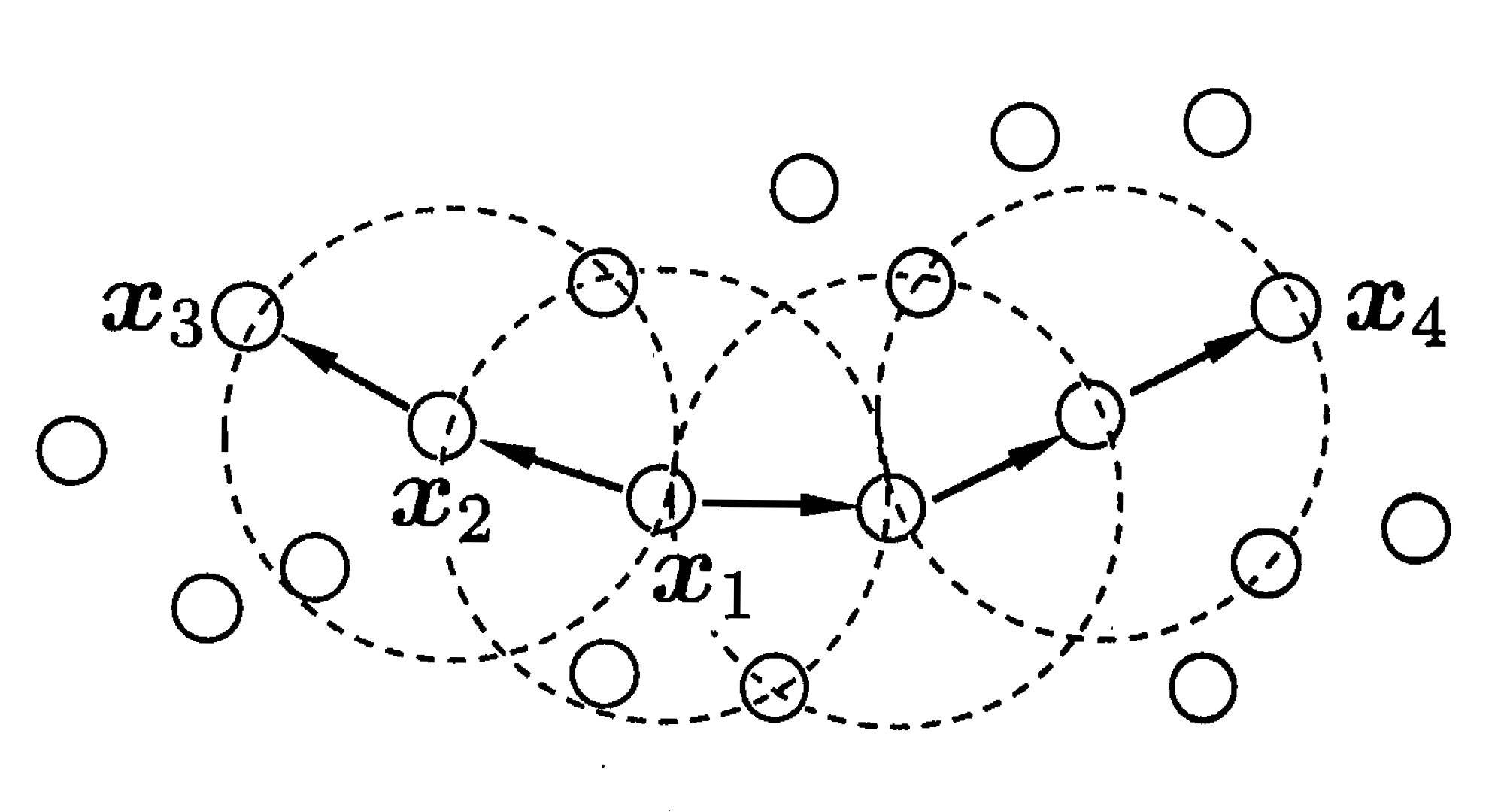
上图直观显示 DBSCAN 中这几个概念:当 MinPts=3 的时候,虚线圆圈为 e 邻域,x1 是核心对象,x2 由 x1 密度直达,x3 由 x1 密度可达,x3 与 x4 密度相连。
根据以上概念,DBSCAN 将簇定义为:由密度可达关系导出的最大的密度相连样本集合。
DBSCAN算法步骤大致描述如下:
对于给定的邻域距离e和邻域最小样本个数MinPts:
- 遍历所有样本,找出所有满足邻域距离e的核心对象的集合;
- 任意选择一个核心对象,找出其所有密度可达的样本并生成聚类簇;
- 从剩余的核心对象中移除2中找到的密度可达的样本;
- 从更新后的核心对象集合重复执行2-3步直到核心对象都被遍历或移除。