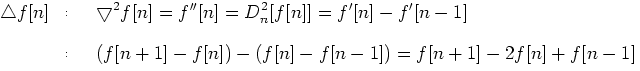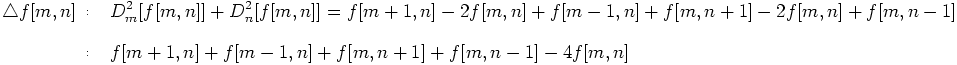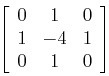图像出增强之锐化---拉普拉斯锐化

（1）拉普拉斯理论

（2）拉普拉斯算子

（3）拉普拉斯实现

--------------------------------------

（1）拉普拉斯理论

　　http://course.cug.edu.cn/pic_ana/wangluoketang/Chapter04/4.2.2.htm

http://blog.sina.com.cn/s/blog_6163bdeb0100h1xf.html

更复杂些的滤波算子一般是先利用高斯滤波来平滑，然后计算其1阶和2阶微分。由于它们滤除高频和低频，因此称为带通滤波器（band-pass filters）。

在介绍具体的带通滤波器前，先介绍必备的图像微分知识。

1 一阶导数

连续函数，其微分可表达为 ，或                         （1.1）

对于离散情况（图像），其导数必须用差分方差来近似，有

                                   ，前向差分 forward differencing                  （1.2）

                                    ，中心差分 central differencing                     （1.3）

实例：技术图像x方向导数

1 2	I = imread('coins.png'); figure; imshow(I); Id = mipforwarddiff(I,'dx'); figure, imshow(Id);

       

    原图像                                                   x方向1阶导数

2 图像梯度（Image Gradient）

图像I的梯度定义为  ，其幅值为 。出于计算性能考虑，幅值也可用 来近似。

Matlab函数

1）gradient：梯度计算

2）quiver：以箭头形状绘制梯度。注意放大下面最右侧图可看到箭头，由于这里计算横竖两个方向的梯度，因此箭头方向都是水平或垂直的。

实例：仍采用上面的原始图像

1 2 3 4 5

I = double(imread('coins.png')); [dx,dy]=gradient(I); magnitudeI=sqrt(dx.^2+dy.^2); figure;imagesc(magnitudeI);colormap(gray);%梯度幅值 hold on;quiver(dx,dy);%叠加梯度方向

         

                         梯度幅值                                   梯度幅值+梯度方向

3 二阶导数

对于一维函数，其二阶导数 ，即 。它的差分函数为

                                                   （3.1）

3.1 普拉斯算子（laplacian operator）

3.1.2 概念

拉普拉斯算子是n维欧式空间的一个二阶微分算子。它定义为两个梯度向量算子的内积

                                  （3.2）

其在二维空间上的公式为：                    （3.3)

对于1维离散情况，其二阶导数变为二阶差分

1）首先，其一阶差分为

2）因此，二阶差分为

           

3）因此，1维拉普拉斯运算可以通过1维卷积核 实现

对于2维离散情况（图像），拉普拉斯算子是2个维上二阶差分的和（见式3.3），其公式为：

   （3.4）

上式对应的卷积核为

                       

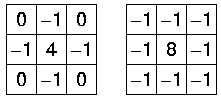
常用的拉普拉斯核有：

                      

3.1.2 应用

拉普拉斯算子会突出像素值快速变化的区域，因此常用于边缘检测。

Matlab里有两个函数

1）del2

计算公式： ，  

2）fspecial：图像处理中一般利用Matlab函数fspecial

h = fspecial('laplacian', alpha) returns a 3-by-3 filter approximating the shape of the two-dimensional Laplacian operator.
The parameter alpha controls the shape of the Laplacian and must be in the range 0.0 to 1.0. The default value for alpha is 0.2.

（2）拉普拉斯算子

 第一个算子核可以用求导查分的出来的系数，是四邻域的，第二个暂时还不晓得怎么的出来的，是8邻域，带斜面效果比第一个好些！

add！ 后面发现一篇文章解释了这个推导过程，还是不明白；

//

对角线方向也可以加入到离散拉普拉斯变换的定义中.只需在式(3.7.4)中添入两项，即两个对角线方向各加一个。每一个新添加项的形式与式(3.7.2)或式(3.7.3)类似，只是其坐标轴的方向沿着对角线方向。由于每个对角线方向上的项还包含一个-2f(x,y)，所以，现在从不同方向的项上减去的总和是-8f(x,y)。执行这一新定义的掩模如图3.39(b)所示。这种掩模对45^o增幅的结果是各向同性的。图3.39所示的另外两个掩模在实践中也经常使用。这两个掩模也是以拉普拉斯变换定义为基础的，只是其中的系数与我们在这里所用到的符号相反而已。正因如此，它们产生等效的结果，但是，当拉普拉斯滤渡后的图像与其他图像合并时(相加或相减)，则必须考虑符号上的差别。 

上面的方程式在下面

http://blog.sina.com.cn/s/blog_6e7e94bc0100o9lr.html

http://www.cnblogs.com/pegasus/archive/2011/05/20/2051780.html

http://www.math.zju.edu.cn/cagd/resources/thesis/MasterThesis_FangHuilan.pdf 网格曲面上离散曲率计算方法的比较与研究 浙江大学数学系的硕士论文，可以挖据资源哦 貌似小猪的毕设就是这个题目

//

（3）拉普拉斯实现

基于模板的：

 /**************************************
********************************
*
* 函数名称：
*     LapTemplate(int inputH, int 
inputW, int inputX0, int inputY0, float 
*     pTemplate, float fCoef)
*
* 参数：
*     int inputH-模板的高度
*     int inputW-模板的宽度
*     int inputX0-模板的中心元素X坐标
*     int inputY0-模板的中心元素Y坐标
*     float *pTemplate-指向模板数组的指针
*     float f-模板系数
*
* 返回值：
*     void
*
* 说明：
*     该函数用指定的模板（任意大小）来对
图像进行操作，参数inputH指定模板
*     的高度，参数inputW指定模板的宽度，
参数inputX0和iinputY0指定模板的中心
*     元素坐标，参数pTemplate指定模板元素，f指定系数
*     拉普拉斯锐化
***********************************
***********************************/
void CImgEnhance::LapTemplate(int 
inputH, int inputW, int inputX0, int 
inputY0, float *pTemplate, float f)
{
unsigned char *pSrc, *pDst; 
int  i,j,k,l;
float value;

if(m_pImgDataOut != NULL)
{
delete []m_pImgDataOut;
m_pImgDataOut = NULL;
}
 int lineByte = (m_imgWidth * 
m_nBitCount / 8 + 3) / 4 * 4;

if(m_nBitCount != 8)
{
AfxMessageBox("只能处理8位灰度图像!");
return ;
}
//创建要复制的图像区域
m_nBitCountOut = m_nBitCount;
int lineByteOut = (m_imgWidth * 
m_nBitCountOut / 8 + 3) / 4 * 4;
if (!m_pImgDataOut)
{
m_pImgDataOut = new unsigned char
[lineByteOut * m_imgHeight];
}

int pixelByte = m_nBitCountOut / 8;
for(i = 0; i < m_imgHeight; i++){
for(j = 0; j < m_imgWidth * pixelByte; j++)
*(m_pImgDataOut + i * lineByteOut + j)
= *(m_pImgData + i * lineByteOut + j);
}

//行处理
for (i = inputY0; i < m_imgHeight - 
inputH + inputY0 + 1; i++)
{
//列处理
for (j = inputX0; j <m_imgwidth <br="" -="">inputW + inputX0 + 1; j++)
{
//指向新DIB第i行第j列像素的指针
pDst = m_pImgDataOut + lineByte * 
(m_imgHeight -1 - i) + j;

value=0;
//计算
for (k = 0; k < inputH; k++)
{
for (l = 0; l < inputW; l++)
{
pSrc = m_pImgData + lineByte * 
(m_imgHeight - 1 - i + inputY0 - k)+ j - inputX0 + l;
//计算加权平均
value += (*pSrc) * pTemplate[k * inputW + l];
}
}
//乘以系数
value *= f;
//取结果的绝对值
value = (float)fabs(value);
if (value > 255)
{
*pDst = 255; 
}
else
{
*pDst = (unsigned char)(value+0.5);
}
}
}
}

http://book.51cto.com/art/200808/84592.htm c++实现

http://dsqiu.iteye.com/blog/1638589

http://www.xuebuyuan.com/1050504.html

http://blog.csdn.net/jia20003/article/details/16369143