题意: 求坐标平面中由【x1,x2】,【y1,y2】中围成的矩形中的所有满足ax+by+c=0的整点的个数。
是使用拓展欧几里德解线性方程的题目,有一些细节需要处理:方程是否有整数解,a,b的系数中为0和为负数的情况。
根据拓展欧几里德定理知道有解时所有的解都是通过解出来的一组基础解(x,y)产生,可以写成这种形式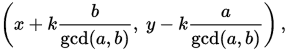
,所以可以先通过x坐标确定出来对应的k值的范围【kx1,kx2】,对应的可以再通过y坐标确定出来【ky1,ky2】,最后两组取交集就是解的总个数。

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <string> 5 #include <queue> 6 #include <list> 7 #include <map> 8 #include <set> 9 #include <stack> 10 #include <cmath> 11 #include <bitset> 12 #include <vector> 13 #include <sstream> 14 #include <cstdlib> 15 #include <algorithm> 16 using namespace std; 17 typedef long long ll; 18 #define fori(i,l,u) for(ll (i)=(ll)(l);(i)<=(ll)(u);++(i)) 19 #define ford(i,l,u) for(ll (i)=(ll)(l);(i)>=(ll)(u);--(i)) 20 #define fir first 21 #define sec second 22 const ll inf=0x3fff3fff3fff3fffll; 23 ll ex_gcd(ll a,ll b,ll &x,ll &y) // ax+by=gcd(a,b) 24 { 25 if(a==0&&b==0) return -1; 26 if(b==0) {x=1;y=0;return a;} 27 ll d=ex_gcd(b,a%b,y,x); 28 y-=a/b*x; 29 return d; 30 } 31 int main() 32 { 33 ios::sync_with_stdio(false); 34 // freopen("local.in","r",stdin); 35 ll T; 36 while(cin>>T){ 37 fori(kase,1,T){ 38 ll a,b,c,x1,x2,y1,y2; 39 cin>>a>>b>>c>>x1>>x2>>y1>>y2; 40 ll x0,y0; 41 if(a<0) {a=-a;ll t=-x1;x1=-x2;x2=t;} 42 if(b<0) {b=-b;ll t=-y1;y1=-y2;y2=t;} 43 c=-c; 44 ll ans=0; 45 if(a==0&&b==0) { 46 if(c==0) ans=(x2-x1+1)*(y2-y1+1); 47 } else if(a==0){ 48 if(c%b==0&&(c/b>=y1&&c/b<=y2)) ans=x2-x1+1; 49 } else if(b==0) { 50 if(c%a==0&&(c/a>=x1&&c/a<=x2)) ans=y2-y1+1; 51 } else { 52 ll d=ex_gcd(a,b,x0,y0); 53 if(c%d==0) { 54 x0=x0*(c/d); y0=y0*(c/d); 55 ll ex=(b/d),ey=(-a/d); 56 ll kx1,kx2; 57 if(ex>0) {kx1=ceil((double(x1-x0))/ex); kx2=floor((double(x2-x0))/ex);} 58 else {kx1=ceil((double(x2-x0))/ex); kx2=floor((double(x1-x0))/ex);} 59 ll ky1,ky2; 60 if(ey>0) {ky1=ceil((double(y1-y0))/ey); ky2=floor((double(y2-y0))/ey);} 61 else {ky1=ceil((double(y2-y0))/ey); ky2=floor((double(y1-y0))/ey);} 62 63 ll lo=max(kx1,ky1),hi=min(kx2,ky2); 64 if(lo<=hi) ans=hi-lo+1; 65 } 66 } 67 cout<<"Case "<<kase<<": "<<ans<<endl; 68 } 69 } 70 71 return 0; 72 }
