堆排序

1、基本思想

堆是一种特殊的树形数据结构，其每个节点都有一个值，通常提到的堆都是指一颗完全二叉树，根结点的值小于（或大于）两个子节点的值，同时，根节点的两个子树也分别是一个堆。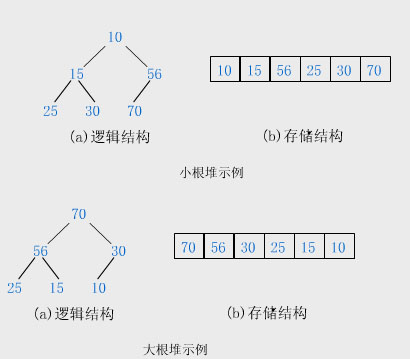 
 
堆排序就是利用堆（假设利用大顶堆）进行排序的方法。它的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根节点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的 n-1 个序列重新构造成一个堆，这样就会得到 n 个元素中次大的值。如此反复执行，便能得到一个有序序列了。 
堆排序的实现需要解决的两个关键问题： 
（1）将一个无序序列构成一个堆。 
（2）输出堆顶元素后，调整剩余元素成为一个新堆。

3.大根堆排序算法的基本操作

① 初始化操作：将R[1..n]构造为初始堆； 
②每一趟排序的基本操作：将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换，然后将新的无序区调整为堆(亦称重建堆)。

注意： 
①只需做n-1趟排序，选出较大的n-1个关键字即可以使得文件递增有序。 
②用小根堆排序与利用大根堆类似，只不过其排序结果是递减有序的。堆排序和直接选择排序相反：在任何时刻堆排序中无序区总是在有序区之前，且有序区是在原向量的尾部由后往前逐步扩大至整个向量为止。

4、Java实现如下

public class HeapSort {
    /**
     * 构建大顶堆
     */
    public static void adjustHeap(int[] a, int i, int len) {
        int temp, j;
        temp = a[i];
        for (j = 2 * i; j < len; j *= 2) {// 沿关键字较大的孩子结点向下筛选
            if (j < len && a[j] < a[j + 1])
                ++j; // j为关键字中较大记录的下标
            if (temp >= a[j])
                break;
            a[i] = a[j];
            i = j;
        }
        a[i] = temp;
    }

    public static void heapSort(int[] a) {
        int i;
        for (i = a.length / 2 - 1; i >= 0; i--) {// 构建一个大顶堆
            adjustHeap(a, i, a.length - 1);
        }
        for (i = a.length - 1; i >= 0; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换
            int temp = a[0];
            a[0] = a[i];
            a[i] = temp;
            adjustHeap(a, 0, i - 1);// 将a中前i-1个记录重新调整为大顶堆
        }
    }

    public static void main(String[] args) {
        int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 };
        heapSort(a);
        System.out.println(Arrays.toString(a));
    }
}