作者:gnuhpc
出处:http://www.cnblogs.com/gnuhpc/
转自:http://www.cnblogs.com/gnuhpc/archive/2012/10/13/2722879.html
1.边缘检测:
边缘检测是图像处理和计算机视觉中的基本问题,边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。这些包括(i)深度上的不连续、(ii)表面方向不连续、(iii)物质属性变化和(iv)场景照明变化。边缘检测是图像处理和计算机视觉中,尤其是特征提取中的一个。
图像边缘检测大幅度地减少了数据量,并且剔除了可以认为不相关的信息,保留了图像重要的结构属性。有许多方法用于边缘检测,它们的绝大部分可以划分为两类:基于查找的一类和基于零穿越的一类。基于查找的方法通过寻找图像一阶导数中的最大和最小值来检测边界,通常是将边界定位在梯度最大的方向(想想一阶导数的含义是图像变化的速度,最大的自然就是变化最大的了)。基于零穿越的方法通过寻找图像二阶导数零穿越来寻找边界,通常是Laplacian过零点或者非线性差分表示的过零点。
2.差分
差分,又名差分函数或差分运算,是数学中的一个概念。它将原函数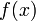 映射到
映射到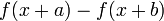 。差分运算,相应于微分运算,是微积分中重要的一个概念。差分的定义分为前向差分和逆向差分两种。
。差分运算,相应于微分运算,是微积分中重要的一个概念。差分的定义分为前向差分和逆向差分两种。
则称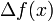 为
为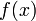 的一阶前向差分。在微积分学中的有限差分(finite differences),前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当
的一阶前向差分。在微积分学中的有限差分(finite differences),前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当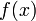 是多项式时,前向差分为Delta算子,一种线性算子。前向差分会将多项式阶数降低1。
是多项式时,前向差分为Delta算子,一种线性算子。前向差分会将多项式阶数降低1。
索贝尔算子(Sobel operator)是图像处理中的算子之一,主要用作边缘检测。在技术上,它是一离散性差分算子,用来运算图像亮度函数的梯度之近似值。在图像的任何一点使用此算子,将会产生对应的梯度矢量或是其法矢量。
该算子包含两组3x3的矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。如果以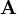 代表原始图像,
代表原始图像,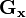 及
及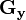 分别代表经横向及纵向边缘检测的图像,其公式如下:
分别代表经横向及纵向边缘检测的图像,其公式如下:
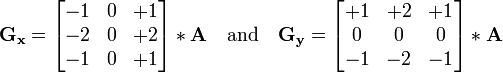
图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合,来计算梯度的大小。
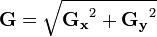
然后可用以下公式计算梯度方向。
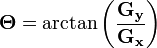
在以上例子中,如果以上的角度Θ等于零,即代表图像该处拥有纵向边缘,左方较右方暗。
4.矩阵卷积
函数矩阵的卷积
定义两个函数矩阵的卷积可以用类似于两个矩阵乘法的运算规则,即将两个元素相乘的符号都用卷积来替换,譬如
5.图像梯度
感性认识:梯度值就是图像灰度值的显著变化的地方。不同的算子对应了不同的求梯度的方法:
以Sobel算子(效果较好)为例:
对于数字图像,可以用一阶差分代替一阶微分;
△xf(x,y)=f(x,y)-f(x-1,y);
△yf(x,y)=f(x,y)-f(x,y-1)
求梯度时对于平方和运算及开方运算,可以用两个分量的绝对值之和表示,即:
G[f(x,y)]={[△xf(x,y)] +[△yf(x,y)] } |△xf(x,y)|+|△yf(x,y)|;
Sobel梯度算子是先做成加权平均,再微分,然后求梯度,即:
△xf(x,y)= f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)- f(x-1,y-1) - 2f(x,y-1) - f(x+1,y-1);
△yf(x,y)= f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)- f(x+1,y-1) - 2f(x+1,y) - f(x+1,y+1);
G[f(x,y)]=|△xf(x,y)|+|△yf(x,y)|;
6.高斯金字塔
对于大小为w×i的图像I,高斯金字塔Gj由I的几个分辨率减小的高斯图像Ii(i是下标,下同)组成,其中,i={0,1,...,j}代表金字塔的级数.图像Ii 的大小为(w/2i)×(h/2i).[2i表示2的i次方]。图像Ii是通过对图像Ii-1(i-1是下标)进行隔行隔列采样而得到的图。
作者:gnuhpc
出处:http://www.cnblogs.com/gnuhpc/
除非另有声明,本网站采用知识共享“署名 2.5 中国大陆”许可协议授权。
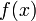 ,如果:
,如果: ,
,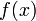 ,如果:
,如果: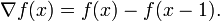 则称
则称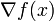 为
为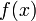 的一阶逆向差分。
的一阶逆向差分。