群
群 = 非空集合 + 二元运算 + 性质
半群
设 为一个非空集合,
上有二元运算
,满足结合律,则称
或
为一个半群。
扩展:
幺元:假设半群 ,若元素
满足
,
,则称
为
的左幺元。同样的可以推广至右幺元。若
既是左幺元又是右幺元,则称
为
的幺元,同时称
为幺半群。
逆元:设 为幺半群,
为幺元,
。若元素
满足
,则称
为
的左逆元。同样可以推广至右逆元。若
既是
的左逆元又是右逆元,则称
为
的一个逆元,将
记为
。
群定义
幺半群 每个元素都可逆,则把
称为群。
第一定义:
从集合观点来看: ,定义一个二元运算
对于
封闭。
- 运算
满足结合律。
里面存着幺元,
。
存在逆元,
使得
。
第二定义:
,定义一个二元运算
对于
封闭。
- 运算
满足结合律。
-
中存在左(右)幺元
,
存在左(右)逆元
,
扩展:
群阶:设 为群,
的阶指的是
中元素的个数,记号为
。
则称为有限群,否则称为无限群。当
时,我们可以用群表表示出来。
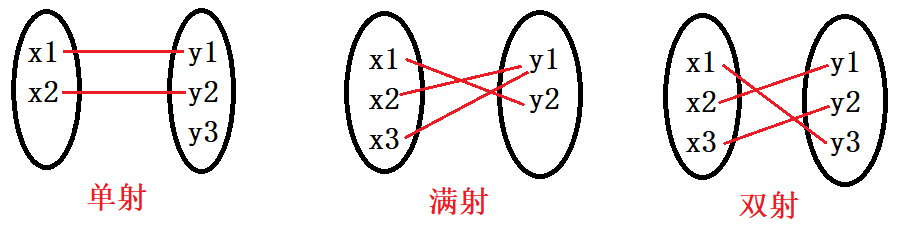
映射
设函数
单射:任给 ,
,若
,则
,称
为单射
满射:任给 ,都存在
使得
, 称
为满射
双射:若 既是单射又是满射,称
为双射,也叫一一对应。
代数运算
设 为三个非空集合,一个映射
,该映射称为
到
的一个代数运算。
如果 ,代数运算
称为
上的二元运算
运算表
,定义
,
运算表如下:
| 1 | 2 | |
| 1 | 奇 | 偶 |
| 2 | 偶 | 奇 |
对角线对称,可以发现这是一个交换的集合,其实可以看到 。所以,交换律其实可以从表中可以看出来。
分类
一个 分类就是将
写成一些不相交的非空子集的并
关系
集合 中一种对两个元素而言的一种性质,使
中任何两个元素要么有关系,要么没关系,二者必居其一。用
表示,
与
有关系
,记为
,无关系
,记为
.
等价关系
设 中定义了关系
,若
满足条件
- 反身性:
.
- 对称性:
.
- 传递性:
则称 为等价关系
等价关系与分类的关系:
等价关系 分类,即
中一个等价关系
决定
的一个分类、
的一个分类决定
中一个等价关系
等价类
设 ,
中有一个等价关系
,
,定义
的等价类
(或称
所在的等价类)。
设 ,
中定义了等价关系
,定义集合
(重复的只取一个)称为
对
的商集合
同余关系
设 ,
中定义了二元运算 "
",有定义了等价关系
,如果
和 "
" 满足条件
,则称
为 "
" 的同余关系
子群
假设 为群,
,若
在
的运算构成群,则称
为
的子群,记为
,注意,这个不是表示小于的意思
假设 ,则
设 ,则下列条件等价:
是
的正规子群,即
;
,其中
(对任何的非空子集
)
不变子群(正规子群)
假设 为群,
,
,则
是一个不变子群,记
判定定理:
1、假设 为群,
,则
当且仅当
,有$ gH{g^{ - 1}} = H$
2、假设 为群,
,则
当且仅当
,有$ g{
m{h}}{g^{ - 1}} in H$
扩展:
1、一个交换群 的每一个子群
都是不变子群
2、平凡子群都是不变子群
平凡子群:设 为群,{e}和
本身是
的平凡子群
陪集
设 为群,
,定义
称为
为代表元的
的一个左陪集,
称为
为代表元的
的一个右陪集;换句话说,一个不变子群
的一个左(右)陪作
的一个陪集
设 为群,
,则关系
为等价关系。
所在的等价类
恰好是
的左陪集
,故
的所有左陪集构成
的一个分类。
商群
定义1:设 ,则等价关系
是
的同余关系
,这个时候,
对于诱导的运算构成一个群,则称
为
的商群,记为
。
定义2:一个群 的一个不变子群
的陪集(关于陪集的乘法)所作成的群叫做一个商群,记为
即:若,
 是群
是群关于其不变子群
的一个陪集分解,对于
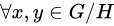 ,定义:
,定义: ,则
,则 关于上述法则作成一个群,叫做群
关于不变子群
的商群
举例: 为
群,
,
,则
为群,
,由
,设
,则
,所以
为模
的剩余类加群,
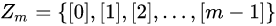
同态和同构
设 ,
为
到
的映射,如果
称
为
到
的同态映射,简称为同态。若同态
为单射,称
为单同态(满射
满同态)。若同态
为双射,则称
为同构,这时称
和
同构,记为
。
扩展:
1、设 为同态,定义
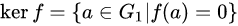 (0指的是
(0指的是 中的0元)称为
的核,换句话说Kerf也就是
中0元的原像
2、 .
3、(群的同态基本定理). 设 的满同态,则
循环群
假设 是一个群,如果存在
,使得
,则
为循环群,记为
,称
为群
的生成元。
举例: 为循环群,
都为生成元
定理:
1、循环群肯定为交换群 (Abel群)。
2、循环群的子群也是循环群。
3、假设 是一个由元
所生成的循环群,那么
的构造完全可以由a的阶来决定:
的阶若是无限的,那么
与整数加群同构
的阶若是一个有限整数m,那么
与模m的剩余类加群同构
即:假设 是一个循环群,若
,则
,若
,则
【
是
的子群形式】。我们可以得到两个循环群同构
它们的阶相同。
4、设 , 则
中存在唯一的
阶子群。
模m的剩余类加群
假设 是一个循环群,
包含模m的m个剩余类,[a]表示a这个整数所在的剩余类,现规定一个代数运算:
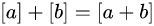 ,对于这种运算
,对于这种运算 所作成一个群,这个群叫做模
的剩余类加群,
变换
变换是一种特殊的映射
一个集合,
到
自己的映射,叫做
的一个变换:
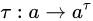
随之对应的 “单射变换”、“满射变换”、“一一变换”
将集合的全体变换作成一个集合
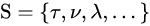 ,在集合
,在集合 上定义一个代数运算:
上定义一个代数运算: ,这种运算也可以看成变换的复合
,这种运算也可以看成变换的复合
这种运算适合结合律: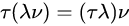
变换群
一个集合的若干个一一变换对于上述的规定的运算所作成的一个群叫做
的一个变换群
定理:
1、(Cayley定理)任何群都与一个变换群同构
2、一个集合的所有的一一变换作成一个变换群G
3、变换群一般不是交换群
置换
一个有限集合的一个一一变换叫做一个置换
置换群
置换群是变换群中的一个特例
一个有限集合的若干个置换作成的一个群叫做一个置换群
一个包含n个元的集合的全体置换作成的群叫做n次对称群,记 
定理:
1、奇置换乘奇置换为偶置换,奇置换与偶置换之积为奇置换,偶置换与偶置换之积为偶置换,奇置换之逆是奇置换,偶置换之逆是偶置换。
2、n次对称群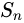 的阶是n!
的阶是n!
3、每一个有限群都与一个置换群同构
4、每一个置换都可以写成不相连的循环置换的乘积
环
加群
一个代数运算是加法的交换群是加群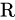
对于加法的单位元为
,称为
的零元;
设 ,
在加法运算下的逆元记为
,记为
的负元。
个
连加记为
;
规定
环定义
一个集合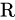 是环,需满足:
是环,需满足:
1、 是个加群,即
是个加群,即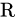 对于一个叫做加法的代数运算作成一个交换群
对于一个叫做加法的代数运算作成一个交换群
2、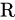 对于另一个叫做乘法的代数运算,是闭的
对于另一个叫做乘法的代数运算,是闭的
3、满足结合率: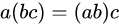
4、满足分配率:
扩展:
1、单位元:环中一个元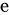 ,满足:
,满足: ,若环中有单位元,则只能有一个;环未必有一个单位元
,若环中有单位元,则只能有一个;环未必有一个单位元
2、逆元:一个有单位元环的一个元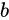 叫做元
叫做元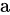 的一个逆元:
的一个逆元: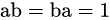 ;环中的元未必有逆元
;环中的元未必有逆元
3、零因子:环中:
 ,
,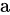 是环的一个左零因子,
是环的一个左零因子,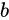 是环的一个右零因子,都简称为零因子
是环的一个右零因子,都简称为零因子
4、一个环 没有零因子
满足左右消去律。
环的特征
设 ,且为无零因子环,1)则
中所有非零元对于
的加法具有相同的阶,2)且当这一个共同的阶有限时必为素数。
设 为无零因子环,若
中非零元的阶为无穷时,则称
的特征
,若
中所有的非零元都是有限
阶的(
为素数),则称
的特征为
。环的特征记为
。
交换环
环叫做交换环,满足:
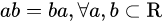
整环
环叫做一个整环,满足:
1、乘法满足交换率:
2、有单位元1:
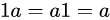
3、没有零因子:
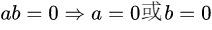
举例:整数环是一个整环
除环
环叫做一个除环,满足:
1、至少包含一个不等于零的元
2、有一个单位元
3、的每一个不等于零的元有一个逆元
扩展:
1、除环是没有零因子的,因为:
2、除环的不等于零的元对于乘法来说作成一个群
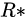 ,叫做除环
,叫做除环的乘群,因为:
(1)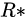 对于乘法来说是闭的
对于乘法来说是闭的
(2)乘法适合结合律
(3)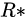 有单位元,就是
有单位元,就是的单位元
(4)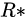 的每一个元有一个逆元
的每一个元有一个逆元
故,一个除环是由两个群,加群和乘群,合成的;分配率好像是一座桥,使得两个群中间之间发生一种联系
子环
设 为环,
是
的非空子集,若
对于
的加法和乘法构成环,则称
为
的子环。
的非空子集
是
的子环充要条件是
。
理想
若子环 满足




若子环 满足


 ,则称是环
,则称是环
若 既是
的左理想又是
的右理想,则称
为
的双边理想,简称理想。属于子环
扩展:
1、 分别是环的最小和最大理想,称为平凡理想
2、设 是一个环,
是
的理想,若
,则
或
,则称
是素理想。
3、 是交换环,
是
的理想,且
, 则
是
的素理想
是整环。
4、 是环
的理想,若
,且不存在
的真理想
,使得
,则称
是极大理想
5、 是交换环R的极大理想
是域
6、交换环R的极大理想一定是素理想。
的极大理想
是域
是整环
是素理想
剩余类环
1、剩余类
一个环和环的理想
,以加法运算,
环作成一个群,
作成
的一个不变子群,这样
的陪集:
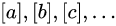 作成
作成的一个分类,把这些分类叫做模
的剩余类
把所有的剩余类作成一个集合叫做 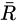 ,并规定两个法则:
,并规定两个法则:

这就是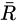 的代数运算
的代数运算
2、若 是一个环,
是它的理想,
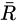 是所有模
是所有模的剩余类作成的集合,那么
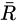 本身也是一个环,且
本身也是一个环,且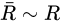 【同态】
【同态】
3、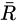 叫做环
叫做环的模
的剩余类环,记

4、若 和
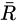 时两个环,且同态,那么这个同态满射的核
时两个环,且同态,那么这个同态满射的核是
的一个理想,且

5、环 到环
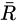 的一个同态满射下:
的一个同态满射下:
(1) 的一个子环
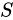 的象
的象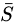 是
是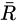 的一个子环
的一个子环
(2) 的一个理想
的象
 是
是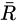 的一个理想
的一个理想
(3) 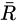 的一个子环
的一个子环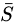 的逆象
的逆象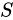 是
是的一个子环
(4) 的一个理想
的一个理想 的象
的象是
的一个理想
环的同态
是两个环,
是
到
的映射,若满足
,
则称 是
到
的同态,若
是单射,则称
是单同态,若
是满射,则称
是满同态,若
是双射,则称
是同构,即
易知, ,
,
是环
的理想。
扩展:
1、 为环,定义
,
是同态,称为零同态
2、 是
到
的同态,
是
到
的同态,则
是
到
的同态,若
是单同态,则
是单同态,若
是满同态,则
是满同态。若
是同构,则
是同构,则
是
到
的同构。
3、 (环的同态基本定理)设 是环
到
的满同态,则
商环
设 是
的理想,在
中定义关系
则关系 是等价关系,且对于环的加法和乘法是同余关系,记
的等价类为
,在商集和
上定义加法和乘法,
则 对于上述运算构成一个环,称为
对于理想
的商环。
扩展: 是交换环,可以推出
是交换环,
是幺环,则
也是幺环,且
是
的单位元。
多项式环
若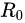 是一个有单位元的交换环,
是一个有单位元的交换环,是
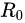 的子环,且包含
的子环,且包含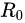 的单位元,现从
的单位元,现从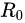 中取出一个元
中取出一个元 ,则
,则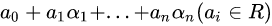 有意义,即也是
有意义,即也是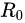 的一个元
的一个元
1、多项式
一个可以写成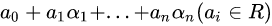 形式的
形式的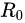 的元叫做
的元叫做上的
 的一个多项式,
的一个多项式, 叫做多项式的系数
叫做多项式的系数
2、现将所有上的
 多项式放到一起,作成一个集合,记
多项式放到一起,作成一个集合,记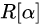 ,且对于加法和乘法都是闭的,也满足结合律和交换律,所以
,且对于加法和乘法都是闭的,也满足结合律和交换律,所以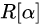 是一个环,故
是一个环,故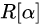 叫做
叫做上的
 的多项式环
的多项式环
3、未定元
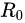 上的一个元
上的一个元 叫做
叫做上的一个未定元,满足:
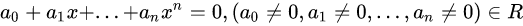
4、一元多项式
令 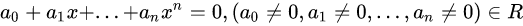 是环
是环上的一个一元多项式,则非负数
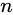 叫做这个多项式的次数
叫做这个多项式的次数
扩展:
若 非零,
,则、
1) 或
2) 或
,等号成立当且仅当
的首项系数
与
的首项系数
的乘积
不为零,特别地,若
为整环,则
也是整环。
现在定义 到
的映射
, 则显然
是环的单同态。由此
可以看成
的一个子环。若
是整环,则整环
的所有单位就是
的所有单位。
整环里的因子分解
唯一分解定理:一个整数可以惟一的写成若干素数的乘积
唯一分解
1、单位
整环 的一个元
 叫做
叫做 的一个单位,若
 有逆元
有逆元
一个整环中至少有两个单位,就是1和-1
性质:
(1)两个单位$alpha 和alpha '$的乘积$alpha alpha '$也是一个单位,单位$alpha$的逆元${alpha ^{{ m{ - }}1}}$也是一个单位
2、相伴元
元b叫做元a的相伴元,若b是a和一个单位 的乘积:$b = alpha a$
的乘积:$b = alpha a$
3、平凡因子
单位以及元a的相伴元b 叫做a的平凡因子,其余a的因子,叫做a的真因子
4、因子
整环的一个元a可以被另外一个元b整除,且有第三个元c,使得:${
m{c}} = ba$,叫a可以被b整除,b是a的因子,记$b|a$
5、素元
整环的一个元p叫做一个素元,满足:p既不是零元也不是单位,且p只有平凡因子
扩展:
(1)单位e同素元p的乘积ep也是一个素元
(2)整环中的一个不等于零的元a有真因子的充分必要条件是:a=bc,b,c都不是单位
(3)假定a≠0,且a有真因子b: a=bc 那么c也是a的真因子
6、唯一分解
一个整数环的一个元a在
的里有唯一分解,满足:
(1)$a = {p_1}{p_2}...{p_r}$(pi是的素元)
(2)若同时$a = {q_1}{q_2}...{q_s}$(qi是的素元)
那么 r=s (个数相同)
唯一分解环
一个整环叫做一个唯一分解环,若:
的每一个既不等于零又不等于单位的元都有唯一分解
一个整环满足以下性质,就是唯一分解环:
1、的每一个既不是零也不是单位的元a都有一个分解:$a = {p_1}{p_2}...{p_r}$(pi是
的素元)
2、的一个素元p若能整除ab,那么p能整除a或者b
则一定是一个唯一分解环
扩展:
1、一个唯一分解环中:若一个素元p能够整除ab,那么p能够整除a或者b
2、最大公因子
元c叫做元${a_1},{a_2},...,{a_n}$的公因子,若c同时能够整除${a_1},{a_2},...,{a_n}$
元 ${a_1},{a_2},...,{a_n}$的一个公因子d叫做${a_1},{a_2},...,{a_n}$的最大公因子,若d能够被${a_1},{a_2},...,{a_n}$的每一个公因子c整除
域
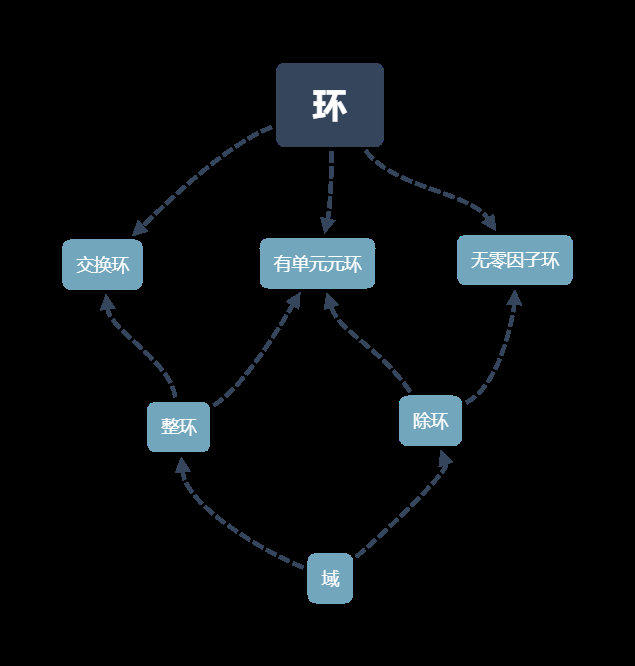
域定义
一个交换除环叫做一个域,一种特殊的环
参考
1、安全六三
2、近世代数基础(张禾瑞)
3、视频
4、简书