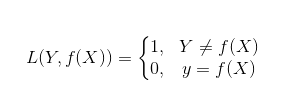损失函数用来估量预测值和真实值的不一致程度。损失函数越小,模型的鲁棒性就越好。损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子:
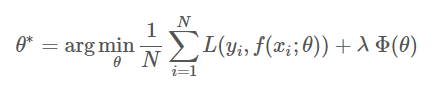
前面的均值函数表示的是经验风险函数,L代表的是损失函数,后面的ΦΦ是正则化项(regularizer)或者叫惩罚项(penalty term),它可以是L1,也可以是L2,或者其他的正则函数。
一、对数损失函数(逻辑回归)
在逻辑回归的推导中,它假设样本服从伯努利分布(0-1分布),然后求得满足该分布的似然函数,接着取对数求极值等等。而逻辑回归并没有求似然函数的极值,而是把极大化当做是一种思想,进而推导出它的经验风险函数为:最小化负的似然函数(即max F(y, f(x)) —> min -F(y, f(x)))。从损失函数的视角来看,它就成了log损失函数了。
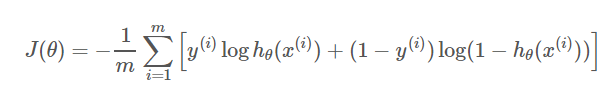
二、平方损失函数(最小二乘法)
最小二乘法是线性回归的一种,OLS将问题转化成了一个凸优化问题。在线性回归中,它假设样本和噪声都服从高斯分布(为什么假设成高斯分布呢?其实这里隐藏了一个小知识点,就是中心极限定理,可以参考【central limit theorem】),最后通过极大似然估计(MLE)可以推导出最小二乘式子。
最小二乘的基本原则是:最优拟合直线应该是使各点到回归直线的距离和最小的直线,即平方和最小。换言之,OLS是基于距离的,而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢(即Mean squared error, MSE),主要有以下几个原因:
- 简单,计算方便;
- 欧氏距离是一种很好的相似性度量标准;
- 在不同的表示域变换后特征性质不变。
平方损失(Square loss)的标准形式如下:
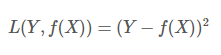
当样本个数为n时,此时的损失函数变为:
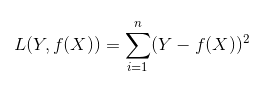
通常会使用均方差(MSE)作为一项衡量指标,公式如下:
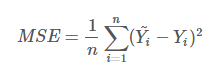
三、指数损失函数(Adaboost)
指数损失函数(exp-loss)的标准形式如下:
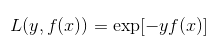
在给定n个样本的情况下,Adaboost的损失函数为:
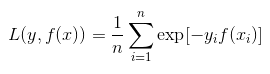
四、hinge损失函数(SVM)
hinge损失函数和SVM是息息相关的:
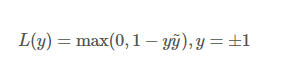
五、绝对值损失函数
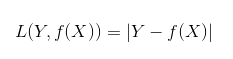
六、0-1损失函数