样条表示这章已经看完,最后的GLU曲面裁剪函数,打算按书中的示例实现一下,其中遇到了几个问题。
先介绍一下GLU曲面裁剪函数的使用方法。
1 裁剪函数是成对出现的: gluBeginTrim和gluEndTrim。它们必须出现并且可以多对存在于gluBeginSurface和gluEndSurface之间。
2 在裁剪函数中间,可以插入B样条分段线型裁剪曲线gluPwlCurve或者B样条一般裁剪曲线gluNurbsCurve或者是它们的混合。
3 必须要注意的是,每一组裁剪函数中间的裁剪曲线,必须是封闭的,不自交并且不与其他曲线相交的。
1 gluBeginSurface(surfName); 2 3 gluBeginTrim(surfName); 4 5 gluPwlCurve(...); 6 gluNurbsCurve(...); 7 .... 8 9 gluEndTrim(surfName); 10 11 gluEndSurface(surfName);
以下是示例程序:
1 先用GLU画出一个坐标范围是(-1.5, -1.5)到(1.5, 1.5)的B样条曲面(其实是个平面)
2 用一条逆时针裁剪曲线表示裁剪保留区域
3 用一条顺时针的组合封闭分段线型曲线和B样条曲线,标出要裁掉的区域

1 #include <GLUT/GLUT.h> 2 #include <iostream> 3 4 GLsizei winWidht = 500, winHeight = 500; 5 6 void init (void) 7 { 8 glClearColor(1.0, 1.0, 1.0, 0.0); 9 10 glMatrixMode(GL_PROJECTION); 11 glLoadIdentity(); 12 gluOrtho2D(-5, 5, -5, 5); 13 } 14 15 void xyCoords (void) 16 { 17 glBegin(GL_LINES); 18 glColor3f(1.0, 0.0, 0.0); // red x axis 19 glVertex2i(-10, 0); 20 glVertex2i(10, 0); 21 glColor3f(0.0, 1.0, 0.0); // green y aixs 22 glVertex2i(0, -10); 23 glVertex2i(0, 10); 24 glEnd(); 25 } 26 27 void errorCallback (void) 28 { 29 std::cout << "errorCallback" << std::endl; 30 } 31 32 void displayFcn1 (void) 33 { 34 glClear(GL_COLOR_BUFFER_BIT); 35 36 glColor3f(0.0, 0.0, 1.0); 37 38 GLfloat ctrlPts [4][4][3] = { 39 {{-3, -3, 0.0}, {-1, -3, 0.0}, {1, -3, 0.0}, {3, -3, 0.0}}, 40 {{-3, -1, 0.0}, {-1, -1, 0.0}, {1, -1, 0.0}, {3, -1, 0.0}}, 41 {{-3, 1, 0.0}, {-1, 1, 0.0}, {1, 1, 0.0}, {3, 1, 0.0}}, 42 {{-3, 3, 0.0}, {-1, 3, 0.0}, {1, 3, 0.0}, {3, 3, 0.0}} 43 }; 44 45 GLUnurbsObj *bezSurface; 46 GLfloat outerTrimPts [5][2] = {{0.0, 0.0}, {1.0, 0.0}, {1.0, 1.0}, {0.0, 1.0}, {0.0, 0.0}}; 47 GLfloat innerTrimPts1 [3][2] = {{0.5, 0.25}, {0.01, 0.02}, {0.2, 0.75}}; 48 GLfloat innerTrimPts2 [4][2] = {{0.2, 0.75}, {0.5, 0.99}, {0.75, 0.5}, {0.5, 0.25}}; 49 GLfloat surfKnots [8] = {0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0}; 50 GLfloat trimCurveKnots [8] = {0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0}; 51 bezSurface = gluNewNurbsRenderer(); 52 gluNurbsCallback(bezSurface, GLU_NURBS_ERROR, errorCallback); 53 54 gluBeginSurface(bezSurface); 55 // gluNurbsProperty(bezSurface, GLU_DISPLAY_MODE, GLU_OUTLINE_POLYGON); // 线框图划分三角形 56 // gluNurbsProperty(bezSurface, GLU_NURBS_MODE, GLU_NURBS_TESSELLATOR); // ???? 细分 不好用 57 58 // ???? 注意 sStride和tStride的顺序,如果颠倒了,对于后面的裁剪坐标,也是颠倒的 59 gluNurbsSurface(bezSurface, 8, surfKnots, 8, surfKnots, 3, 12, &ctrlPts[0][0][0], 4, 4, GL_MAP2_VERTEX_3); 60 61 // ???? 必须先提供一个单位正方形的逆时针区域,是确保所有的图案都能正常显示 62 // http://csweb.cs.wfu.edu/~torgerse/Kokua/Irix_6.5.21_doc_cd/usr/share/Insight/library/SGI_bookshelves/SGI_Developer/books/OpenGL_PG/sgi_html/ch13.html 63 // counterclockwise around the entire unit square of parametric space. This ensures that everything is drawn, provided it isn't removed by a clockwise trimming curve inside of it. 64 gluBeginTrim(bezSurface); 65 gluPwlCurve(bezSurface, 5, &outerTrimPts[0][0], 2, GLU_MAP1_TRIM_2); 66 gluEndTrim(bezSurface); 67 68 // 注意 1 裁剪曲线的坐标设置,必须按照顺时针,最后必须封闭 69 // ???? 注意 2 根据逆时针的坐标范围,整个裁剪区域被看做(0,0)到(1,1)的一个区域,裁剪曲线的坐标必须在0-1之间,并且不能等于0和1,否则会将所有区域都裁减掉 70 gluBeginTrim(bezSurface); 71 gluNurbsCurve(bezSurface, 8, trimCurveKnots, 2, &innerTrimPts2[0][0], 4, GLU_MAP1_TRIM_2); 72 gluPwlCurve(bezSurface, 3, &innerTrimPts1[0][0], 2, GLU_MAP1_TRIM_2); 73 gluEndTrim(bezSurface); 74 75 gluEndSurface(bezSurface); 76 77 xyCoords(); 78 79 glFlush(); 80 } 81 82 void winReshapeFcn (GLint newWidth, GLint newHeight) 83 { 84 glViewport(0, 0, newWidth, newHeight); 85 } 86 87 int main(int argc, char * argv[]) 88 { 89 glutInit(&argc, argv); 90 glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); 91 glutInitWindowSize(winWidht, winHeight); 92 glutInitWindowPosition(100, 100); 93 glutCreateWindow("OpenGL Bézier Curve Surface"); 94 95 init(); 96 glutDisplayFunc(displayFcn1); 97 glutReshapeFunc(winReshapeFcn); 98 glutMainLoop(); 99 100 return 0; 101 }
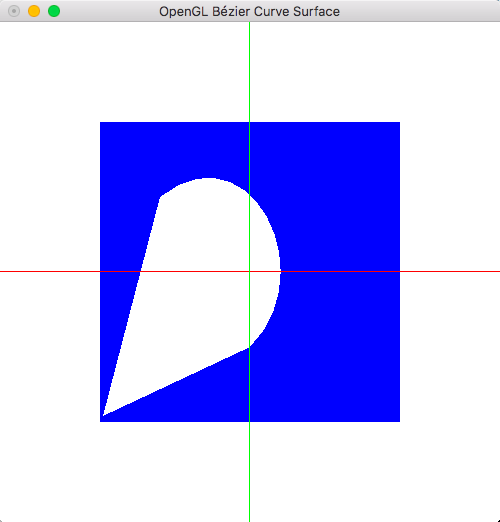
图0
其中,遇到的几个问题是:
1 逆时针裁剪曲线,我尝试过非矩形的情况,也尝试了范围不是(0,0)到(1,1)的范围,但最终的效果是:(0,0)到(1,1)的单位逆时针曲线就可以保留整个曲面,即使整个逆时针裁剪曲线再大,也只是全部显示曲面。当整个逆时针裁剪曲线小于(0,0)到(1,1)的区间时,才能裁剪保留曲面的一部分。
“counterclockwise around the entire unit square of parametric space. This ensures that everything is drawn, provided it isn't removed by a clockwise trimming curve inside of it.”
例如:曲面是(-1.5,-1.5)到(1.5,1.5)的3*3曲面,如果将第一个逆时针裁剪曲线规划为1*1的单位矩形,那么3*3的曲面将全部保留;假如将第一个裁剪曲线的坐标设置为: (0.2,0.0) (0.8,0.0) (1.0, 1.0) (0.0,1.0) (0.2, 0.0)即为一个倒梯形,那么保留下来的曲面将是区域(-0.9, -1.5) (0.9, -1.5) (1.5, 1.5) (-1.5, 1.5)这样的倒梯形。

图1
2 这时再添加顺时针裁剪曲线时,可用的坐标范围即是前面逆时针规定的范围,但不能超过或者等于边界坐标。一旦顺时针裁剪坐标点与逆时针的裁剪曲线边界重合,则会返回error。并且整个曲面都无法正确显示。
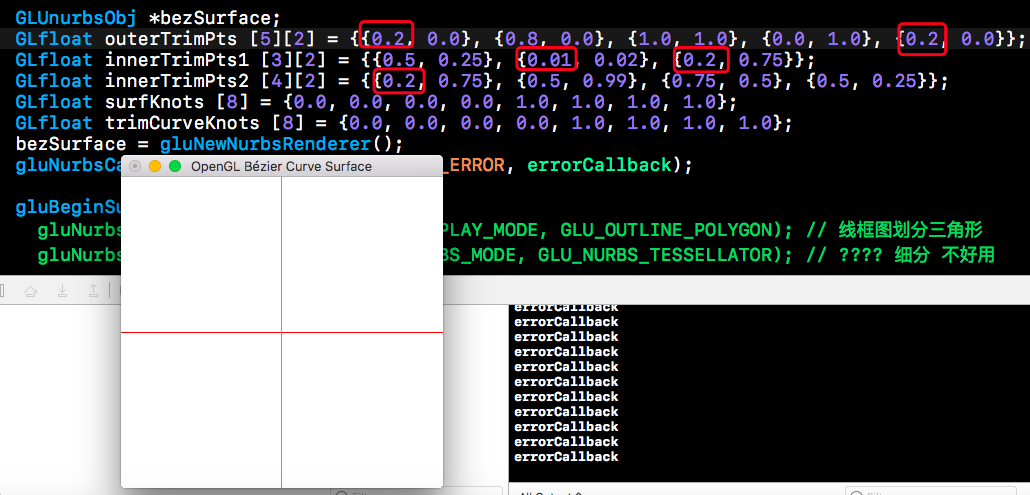
图2
3 如果添加顺时针裁剪曲线,之前必须要逆时针的裁剪区域,否则也会报错。
4 gluNurbsSurface函数,其中注意sStride和tStride的顺序。如果sStride=3,tStride=12,即为u方向连续控制点的坐标以行来读取ctrlPts内容,v方向连续控制点的坐标以列方向为读取方向。即u方向是对应裁剪区域的x轴,而v方向对应裁剪区域的y轴(不很确定是不是这个理解)。那么之后的裁剪坐标的第一个值与sStride方向的坐标对应,而第二个值与tStride方向的坐标对应。加入替换了tStride和sStride的值,那么裁剪掉的内容与原内容是相对轴y=x是对称的。
extern void gluNurbsSurface (GLUnurbs* nurb, GLint sKnotCount, GLfloat* sKnots, GLint tKnotCount, GLfloat* tKnots, GLint sStride, GLint tStride, GLfloat* control, GLint sOrder, GLint tOrder, GLenum type) OPENGL_DEPRECATED(10_0, 10_9);
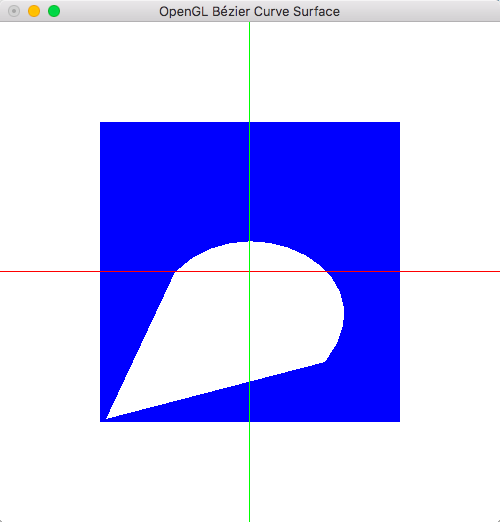
图3 sStride = 12, tStride = 3的才见情况
感觉很多内容理解的不是很透彻,样条曲线这章花了很多时间看,但还是一知半解。在这里列出本章还未解决的几个问题:
1 相邻曲线段的一阶几何连续性,表示一阶导数在两条相邻曲线段的交点处成比例,但不一定相等。这个比例是谁与谁的比例?
2 样条曲线可用于模拟动画路径,相机路径等,是用按代码实现的曲线路径做运动效率高还是美术在Unity中做好的animation效率更高?
3 周期性三次B样条在四个连续控制点上的边界条件P(0) = 1/6(p0 + 4p1 + p2), P(1) = 1/6(p1 + 4p2 +p3), P'(0) = 1/2(p2-p1), P'(1) = 1/2(p3-p1)是如何得到的?
4 样条表示之间的转换: P(u) = U•Mspline1•Mgeom1 = U•Mspline2•Mgeom2 = U•Mspline2•(M-1spline2•Mspline1)•Mgeom1,Ms1,s2 = M-1spline2•Mspline1。书上说这个Ms1,s2是从第一个样条表达式转变到第二个表达式的变换矩阵,即Mspline1 = Mspline2•Ms1,s2,这难道不是第二个样条表达式转变到第一个表达式的变换矩阵吗?
5 递归样条细分方法:取中间点切开原三次Bézier曲线(控制点是p0, p1, p2, p3),左右两段分别构造Bézier样条,获取新控制点的坐标,结果是:p1,0 = p0, p1,1 = 1/2(p0 + p1), p1,2 = 1/4(p0+2p1+p2), p1,3 = 1/8(p0+3p1+3p2+p3)。 在假设:3(p1,1-p1,0) = 1/2(P'(0)) = 1/2•3(p1-p0)的情况下可以推导出上述坐标,但这个假设为什么成立?是Bézier样条曲线的性质决定的吗?
