一.题目
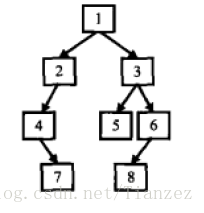
输入某二叉树的前序遍历和中序遍历结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{ 1, 2, 4, 7, 3, 5, 6, 8 }和中序遍历序列{ 4, 7, 2, 1, 5, 3, 8, 6 },则重建的二叉树如图所示:
二.思路
首先根据前序遍历序列找到根节点(序列第一个元素即为根节点),然后在中序遍历中找到根节点位置,然后递归确定左子树和右子树,即可完成二叉树的构建。
三.代码
struct BinaryTreeNode{ int m_nValue; BinaryTreeNode* m_pLeft; BinaryTreeNode* m_pRight; } BinaryTree* Construc(int* preorder,int* inorder,int length){ if(preorder == nullptr || inorder == nullptr || length <= 0) return nullptr; return ConstrucCore(preorder,preorder+length-1.inorder,inorder+length-1); } BinaryTreeNode* ConstrucCore(int* startPreorder,int* endPreorder,int* startInorder,int* endInorder){ //确定根节点 int rootValue = startPreorder[0]; BinaryTreeNode* root = new BinaryTreeNode(); root->m_nValue = rootValue; root->m_pLeft = root->m_pRight = nullptr; if(stratPreorder == endPreorder){ if(startInorder == endInorder) return root; else throw std::exception("Invalid input."); } //在中序遍历中找到根节点 int* rootInorder = startInorder; while(rootInorder <= endInorder && *rootInorder != rootValue) ++rootInorder; if(rootInorder == endInorder && *rootInorder != rootValue) throw std::exception("Invalid input."); int leftLength = rootInorder - startInorder; int* leftPreorderEnd = startPreorder + leftLength; //建立左子树 if(leftLength > 0) root->m_pLeft = ConstrucCore(startPreorder+1,leftPreorderEnd,startInorder,rootInorder-1); //建立右子树 if(leftLength < endPreorder - startPreorder) root->m_pRight = ConstrucCore(leftPreorderEnd+1,endPreorder,rootInorder+1,endInorder); return root; }
四.本题考点
- 考查应聘者对二叉树的前序遍历和中序遍历的理解程度。只有对二叉树的不同遍历算法有了深刻的理解,应聘者才有可能在遍历序列中划分出左右子树对应的子序列。
- 考查应聘者分析复杂问题的能力。我们把构建二叉树的大问题分解为构建左右子树的两个小问题。我们发现小问题和大问题在本质上是一致的,因此可以用递归的方式解决。