Problem Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
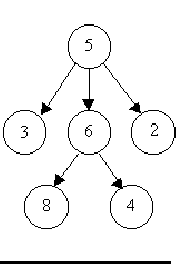
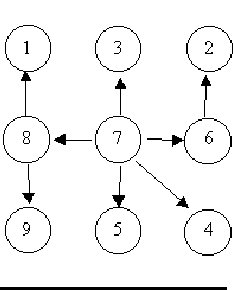
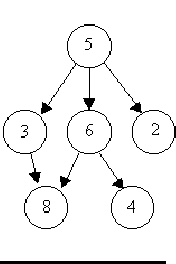
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
http://acm.hdu.edu.cn/showproblem.php?pid=1325

1 #include <iostream> 2 #include <stdio.h> 3 #include <map> 4 using namespace std; 5 6 map<int,int>my_map; 7 map<int,int>my_map2; 8 int f[111111]; 9 int s; 10 int cnt; 11 int sum; 12 13 void init() 14 { 15 int i; 16 for(i=1;i<=100000;i++) 17 { 18 f[i]=i; 19 } 20 my_map.clear(); 21 my_map2.clear(); 22 s=0; 23 cnt=0; 24 sum=0; 25 } 26 27 int find(int x) 28 { 29 if(x==f[x]) 30 { 31 return x; 32 } 33 int t=find(f[x]); 34 f[x]=t; 35 return t; 36 } 37 38 void Union(int a,int b) 39 { 40 f[b]=a; 41 } 42 43 int main() 44 { 45 int a,b; 46 bool flag=false; 47 init(); 48 int count=1; 49 while(~scanf("%d%d",&a,&b)) 50 { 51 if(a==0 && b==0) 52 { 53 if(flag) 54 { 55 printf("Case %d is not a tree.\n",count++); 56 flag=false; 57 } 58 else 59 { 60 if((sum==(cnt-1) && s==(cnt-1)) || (sum==0 && cnt==0)) 61 { 62 printf("Case %d is a tree.\n",count++); 63 } 64 else 65 { 66 printf("Case %d is not a tree.\n",count++); 67 } 68 } 69 init(); 70 continue; 71 } 72 if(a<0 && b<0) 73 { 74 break; 75 } 76 if(!my_map[a]) 77 { 78 my_map[a]++; 79 cnt++; 80 } 81 if(!my_map2[b]) 82 { 83 my_map2[b]++; 84 s++; 85 } 86 if(!my_map[b]) 87 { 88 my_map[b]++; 89 cnt++; 90 } 91 92 int x,y; 93 if(a==b) 94 continue; 95 x=find(a); 96 y=find(b); 97 if(x==y) 98 { 99 flag=true; 100 } 101 else 102 { 103 Union(x,y); 104 sum++; 105 } 106 } 107 return 0; 108 }
并查集题目;
值得注意几点:
1、判断是否出现环,使用并查集模板可以实现。
2、判断是否N个点有且仅有N-1条边。
3、题目要求除根节点外,所有的节点都必须有且仅有一条边指向该节点。
4、从根节点可以通过箭头指向访问到每一个节点,也就是第二条注意说的,必须是联通的。
