二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点:
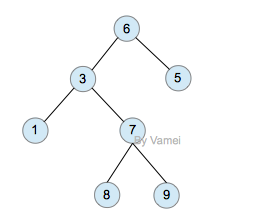
二叉树
由于二叉树的子节点数目确定,所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点,右子节点是右子树的根节点。
如果我们给二叉树加一个额外的条件,就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求:每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大。
(如果我们假设树中没有重复的元素,那么上述要求可以写成:每个节点比它左子树的任意节点大,而且比它右子树的任意节点小)
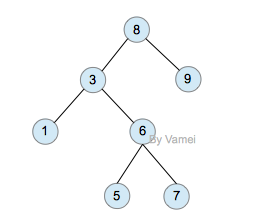
二叉搜索树,注意树中元素的大小
二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候,我们可以将x和根节点比较:
1. 如果x等于根节点,那么找到x,停止搜索 (终止条件)
2. 如果x小于根节点,那么搜索左子树
3. 如果x大于根节点,那么搜索右子树
二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n,最少为log(n)。
下面是用java实现的二叉搜索树,并有搜索,插入,删除,寻找最大最小节点的操作。
删除节点相对比较复杂。删除节点后,有时需要进行一定的调整,以恢复二叉搜索树的性质(每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大)。
- 叶节点可以直接删除。
- 删除非叶节点时,比如下图中的节点8,我们可以删除左子树中最大的元素(或者右树中最大的元素),用删除的节点来补充元素8产生的空缺。但该元素可能也不是叶节点,所以它所产生的空缺需要其他元素补充…… 直到最后删除一个叶节点。上述过程可以递归实现。
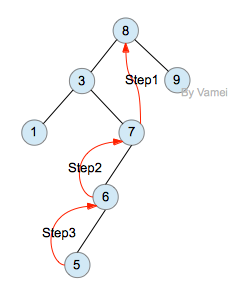
删除节点
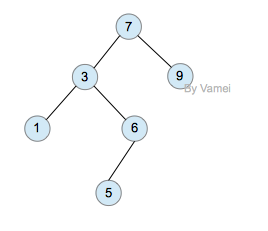
删除节点后的二叉搜索树
import java.util.ArrayList;
import java.util.List;
public class BinarySearchTree {
// 树的根结点
private TreeNode root = null;
// 遍历结点列表
private List<TreeNode> nodelist = new ArrayList<TreeNode>();
private class TreeNode {
private int key;
private TreeNode leftChild;
private TreeNode rightChild;
private TreeNode parent;
public TreeNode(int key, TreeNode leftChild, TreeNode rightChild,
TreeNode parent) {
this.key = key;
this.leftChild = leftChild;
this.rightChild = rightChild;
this.parent = parent;
}
public int getKey() {
return key;
}
public String toString() {
String leftkey = (leftChild == null ? "" : String
.valueOf(leftChild.key));
String rightkey = (rightChild == null ? "" : String
.valueOf(rightChild.key));
return "(" + leftkey + " , " + key + " , " + rightkey + ")";
}
}
/**
* isEmpty: 判断二叉查找树是否为空;若为空,返回 true ,否则返回 false .
*
*/
public boolean isEmpty() {
if (root == null) {
return true;
} else {
return false;
}
}
/**
* TreeEmpty: 对于某些二叉查找树操作(比如删除关键字)来说,若树为空,则抛出异常。
*/
public void TreeEmpty() throws Exception {
if (isEmpty()) {
throw new Exception("树为空!");
}
}
/**
* search: 在二叉查找树中查询给定关键字
*
* @param key
* 给定关键字
* @return 匹配给定关键字的树结点
*/
public TreeNode search(int key) {
TreeNode pNode = root;
while (pNode != null && pNode.key != key) {
if (key < pNode.key) {
pNode = pNode.leftChild;
} else {
pNode = pNode.rightChild;
}
}
return pNode;
}
/**
* minElemNode: 获取二叉查找树中的最小关键字结点
*
* @return 二叉查找树的最小关键字结点
* @throws Exception
* 若树为空,则抛出异常
*/
public TreeNode minElemNode(TreeNode node) throws Exception {
if (node == null) {
throw new Exception("树为空!");
}
TreeNode pNode = node;
while (pNode.leftChild != null) {
pNode = pNode.leftChild;
}
return pNode;
}
/**
* maxElemNode: 获取二叉查找树中的最大关键字结点
*
* @return 二叉查找树的最大关键字结点
* @throws Exception
* 若树为空,则抛出异常
*/
public TreeNode maxElemNode(TreeNode node) throws Exception {
if (node == null) {
throw new Exception("树为空!");
}
TreeNode pNode = node;
while (pNode.rightChild != null) {
pNode = pNode.rightChild;
}
return pNode;
}
/**
* successor: 获取给定结点在中序遍历顺序下的后继结点
*
* @param node
* 给定树中的结点
* @return 若该结点存在中序遍历顺序下的后继结点,则返回其后继结点;否则返回 null
* @throws Exception
*/
public TreeNode successor(TreeNode node) throws Exception {
if (node == null) {
return null;
}
// 若该结点的右子树不为空,则其后继结点就是右子树中的最小关键字结点
if (node.rightChild != null) {
return minElemNode(node.rightChild);
}
// 若该结点右子树为空
TreeNode parentNode = node.parent;
while (parentNode != null && node == parentNode.rightChild) {
node = parentNode;
parentNode = parentNode.parent;
}
return parentNode;
}
/**
* precessor: 获取给定结点在中序遍历顺序下的前趋结点
*
* @param node
* 给定树中的结点
* @return 若该结点存在中序遍历顺序下的前趋结点,则返回其前趋结点;否则返回 null
* @throws Exception
*/
public TreeNode precessor(TreeNode node) throws Exception {
if (node == null) {
return null;
}
// 若该结点的左子树不为空,则其前趋结点就是左子树中的最大关键字结点
if (node.leftChild != null) {
return maxElemNode(node.leftChild);
}
// 若该结点左子树为空
TreeNode parentNode = node.parent;
while (parentNode != null && node == parentNode.leftChild) {
node = parentNode;
parentNode = parentNode.parent;
}
return parentNode;
}
/**
* insert: 将给定关键字插入到二叉查找树中
*
* @param key
* 给定关键字
*/
public void insert(int key) {
TreeNode parentNode = null;
TreeNode newNode = new TreeNode(key, null, null, null);
TreeNode pNode = root;
if (root == null) {
root = newNode;
return;
}
while (pNode != null) {
parentNode = pNode;
if (key < pNode.key) {
pNode = pNode.leftChild;
} else if (key > pNode.key) {
pNode = pNode.rightChild;
} else {
// 树中已存在匹配给定关键字的结点,则什么都不做直接返回
return;
}
}
if (key < parentNode.key) {
parentNode.leftChild = newNode;
newNode.parent = parentNode;
} else {
parentNode.rightChild = newNode;
newNode.parent = parentNode;
}
}
/**
* insert: 从二叉查找树中删除匹配给定关键字相应的树结点
*
* @param key
* 给定关键字
*/
public void delete(int key) throws Exception {
TreeNode pNode = search(key);
if (pNode == null) {
throw new Exception("树中不存在要删除的关键字!");
}
delete(pNode);
}
/**
* delete: 从二叉查找树中删除给定的结点.
*
* @param pNode
* 要删除的结点
*
* 前置条件: 给定结点在二叉查找树中已经存在
* @throws Exception
*/
private void delete(TreeNode pNode) throws Exception {
if (pNode == null) {
return;
}
if (pNode.leftChild == null && pNode.rightChild == null) { // 该结点既无左孩子结点,也无右孩子结点
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = null;
} else {
parentNode.rightChild = null;
}
return;
}
if (pNode.leftChild == null && pNode.rightChild != null) { // 该结点左孩子结点为空,右孩子结点非空
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = pNode.rightChild;
pNode.rightChild.parent = parentNode;
} else {
parentNode.rightChild = pNode.rightChild;
pNode.rightChild.parent = parentNode;
}
return;
}
if (pNode.leftChild != null && pNode.rightChild == null) { // 该结点左孩子结点非空,右孩子结点为空
TreeNode parentNode = pNode.parent;
if (pNode == parentNode.leftChild) {
parentNode.leftChild = pNode.leftChild;
pNode.rightChild.parent = parentNode;
} else {
parentNode.rightChild = pNode.leftChild;
pNode.rightChild.parent = parentNode;
}
return;
}
// 该结点左右孩子结点均非空,则删除该结点的后继结点,并用该后继结点取代该结点
TreeNode successorNode = successor(pNode);
delete(successorNode);
pNode.key = successorNode.key;
}
/**
* inOrderTraverseList: 获得二叉查找树的中序遍历结点列表
*
* @return 二叉查找树的中序遍历结点列表
*/
public List<TreeNode> inOrderTraverseList() {
if (nodelist != null) {
nodelist.clear();
}
inOrderTraverse(root);
return nodelist;
}
/**
* inOrderTraverse: 对给定二叉查找树进行中序遍历
*
* @param root
* 给定二叉查找树的根结点
*/
private void inOrderTraverse(TreeNode root) {
if (root != null) {
inOrderTraverse(root.leftChild);
nodelist.add(root);
inOrderTraverse(root.rightChild);
}
}
/**
* toStringOfOrderList: 获取二叉查找树中关键字的有序列表
*
* @return 二叉查找树中关键字的有序列表
*/
public String toStringOfOrderList() {
StringBuilder sbBuilder = new StringBuilder(" [ ");
for (TreeNode p : inOrderTraverseList()) {
sbBuilder.append(p.key);
sbBuilder.append(" ");
}
sbBuilder.append("]");
return sbBuilder.toString();
}
/**
* 获取该二叉查找树的字符串表示
*/
public String toString() {
StringBuilder sbBuilder = new StringBuilder(" [ ");
for (TreeNode p : inOrderTraverseList()) {
sbBuilder.append(p);
sbBuilder.append(" ");
}
sbBuilder.append("]");
return sbBuilder.toString();
}
public TreeNode getRoot() {
return root;
}
public static void testNode(BinarySearchTree bst, TreeNode pNode)
throws Exception {
System.out.println("本结点: " + pNode);
System.out.println("前趋结点: " + bst.precessor(pNode));
System.out.println("后继结点: " + bst.successor(pNode));
}
public static void testTraverse(BinarySearchTree bst) {
System.out.println("二叉树遍历:" + bst);
System.out.println("二叉查找树转换为有序列表: " + bst.toStringOfOrderList());
}
public static void main(String[] args) {
try {
BinarySearchTree bst = new BinarySearchTree();
System.out.println("查找树是否为空? " + (bst.isEmpty() ? "是" : "否"));
int[] keys = new int[] { 15, 6, 18, 3, 7, 13, 20, 2, 9, 4 };
for (int key : keys) {
bst.insert(key);
}
System.out.println("查找树是否为空? " + (bst.isEmpty() ? "是" : "否"));
TreeNode minkeyNode = bst.minElemNode(bst.getRoot());
System.out.println("最小关键字: " + minkeyNode.getKey());
testNode(bst, minkeyNode);
TreeNode maxKeyNode = bst.maxElemNode(bst.getRoot());
System.out.println("最大关键字: " + maxKeyNode.getKey());
testNode(bst, maxKeyNode);
System.out.println("根结点关键字: " + bst.getRoot().getKey());
testNode(bst, bst.getRoot());
testTraverse(bst);
System.out.println("****************************** ");
testTraverse(bst);
} catch (Exception e) {
System.out.println(e.getMessage());
e.printStackTrace();
}
}
}