DNN

　　 

 

DNN

一、感知机

我们介绍过感知机的模型，它是一个有若干输入和一个输出的模型，如下图:

 

 

输出:

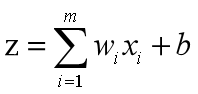
激活函数：

 

从而得到我们想要的输出结果1或者-1。

这个模型只能用于二元分类，且无法学习比较复杂的非线性模型，因此在工业界无法使用。

 

二、DNN

2.1 DNN介绍

 

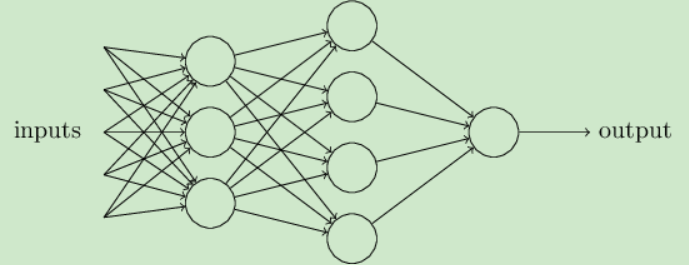
DNN是深度神经网络，其实就是一个多层感知机，DNN相对于感知机的区别：

• 加入了隐藏层
• 输出层的神经元不止一个
• 扩展了激活函数，如sigmod,tanx,softmax,ReLU

2.2 DNN前向算法

前向传播实际上就是利用上一层的输出计算下层的输出。

表示第l-1层的第k个神经元指向第l层的第j个神经元的权重。

 

前向传播算法

假设第l-1层共有m个神经元，则对于第l层的第j个神经元的输出，我们有：

从上面可以看出，使用代数法一个个的表示输出比较复杂，而如果使用矩阵法则比较的简洁。假设第l-1层共有m个神经元，而第l层共有n个神经元，则第l层的线性系数W组成了一个n*m的矩阵, 第l层的偏倚b组成了一个n*1的向量b₁,第l-1层的的输出a组成了一个m*1的向量a^l-1，第l层的的未激活前线性输出z组成了一个n*1的向量z^l ，第l层的的输出a组成了一个n*a的向量a^l。则用矩阵法表示，第l层的输出为：

2.3  DNN反向算法

2.3.1 DNN反向传播算法思路

在进行DNN反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问：训练样本计算出的输出是怎么得来的？这个输出是随机选择一系列W,b,用我们上一节的前向传播算法计算出来的。即通过一系列的计算：。计算到输出层第L层对应的aL即为前向传播算法计算出来的输出。

输出层损失函数：

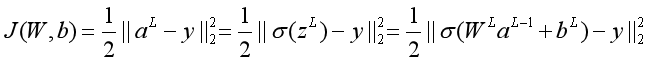
求解输出层对W,b的梯度：

现在求解任意一层对W,b的梯度：

记：

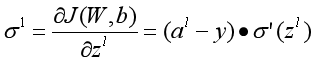
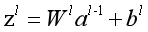
则：

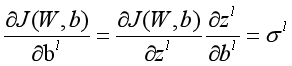
现在只需求出即可

因为：

所以：

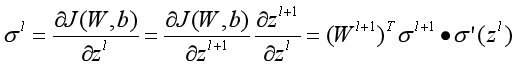
2.3.2 DNN反向传播算法过程总结

现在我们总结下DNN反向传播算法的过程。由于梯度下降法有批量（Batch），小批量(mini-Batch)，随机三个变种，为了简化描述，这里我们以最基本的批量梯度下降法为例来描述反向传播算法。实际上在业界使用最多的是mini-Batch的梯度下降法。不过区别仅仅在于迭代时训练样本的选择而已。

输入: 总层数L，以及各隐藏层与输出层的神经元个数，激活函数，损失函数，迭代步长α,最大迭代次数MAX与停止迭代阈值ϵ，输入的m个训练样本

输出：各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b

算法如下：

1）初始化各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b的值为一个随机值。

2）for iter to 1 to MAX：

　　2-1) for i =1 to m：

　　　　a) 将DNN输入设置为x₁

　　　　b) for l=2 to L，进行前向传播算法计算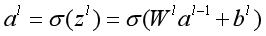

　　　　c) 通过损失函数计算输出层的

　　　　d) for l= L-1 to 2, 进行反向传播算法计算

 　　　

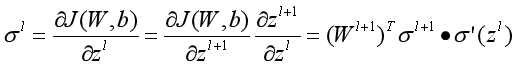
　　2-2) for l= 2 to L，更新第l层的W^l,b^l:

 　　　

　　　 　

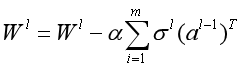
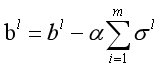
　　2-3) 如果所有W，b的变化值都小于停止迭代阈值ϵ，则跳出迭代循环到步骤3）。

3）输出各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b。

参考资料

1） Neural Networks and Deep Learning by By Michael Nielsen

2） Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville

3） UFLDL Tutorial