本文通过多项式曲线拟合的问题来解释L2正则化的数学含义，既为何选择w*较小的模型。详细内容如下：
1.数据生成
有一组数据，按照的函数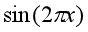
生成，同事有一写随机噪声。
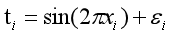
2. 模型
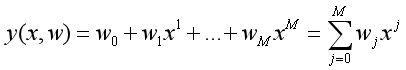
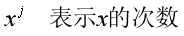
3. 误差函数
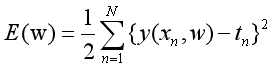
E(w)是w的二次函数，故而存在最小值（当取w*时有最小值），当M取不同的值的时候，可以得到不同的模型，而这些模型有不同的泛化能力，如下图所示。
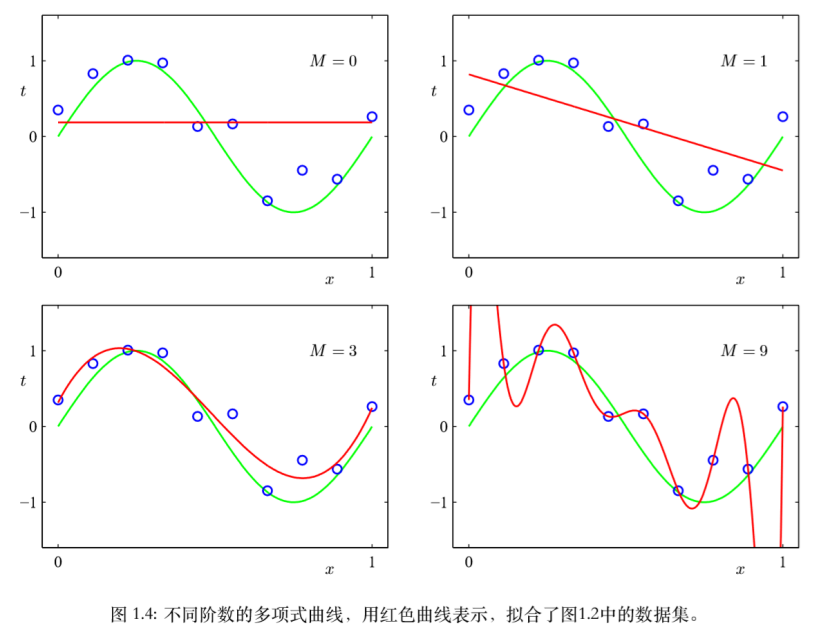
选择阶数M也是一个问题，这个问题叫模型选择。当M=0,1时，模型过于简单，多项式对数据的拟合效果较差，很难表示模型
。当M=3时，多项式很好的拟合了函数
，M=9时，E(w*) = 0，但是且过拟合了。目标是通过对新数据的预测，使的测试集上E(w*)尽可能的小。
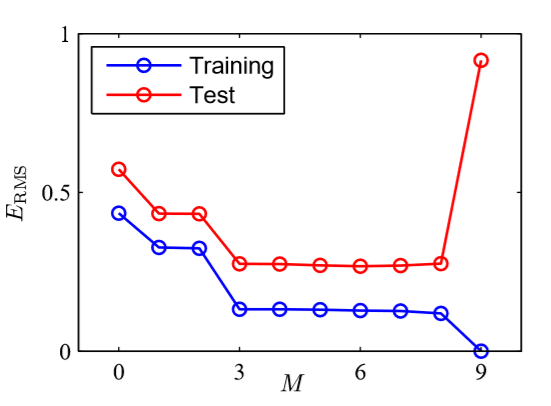
当M取不同的值时，训练误差与测试误差如下图所示，由下图可值，当M=3,4,5,6,7,8时，模型具有很好的泛化能力。
当M取不同的值时，不同阶数的系数如下图：
由上图可知，随着M的增加，w*剧烈的增大了。当M=9时，w*取了很大的值，并且此时，训练误差与测试误差有很大的差距，说明模型过拟合了。当M=9时，让w取相当大的正数或是相当大的负数，多项式可以精确的与数据匹配，即：更大的M值，更灵活的多项式被过分的调参，使得多项式被调成了与目标值的随机噪声相符合，既模型过于复杂。
考察模型的行为随着训练集规模的变化情况，当数据集的规模变大的时候，过拟合的问题变得不那么严重。如下图：
对于M=9的多项式，M=15(左图)，M=100(右图)通过最小化平方和误差函数得到的解，显示，训练集的增大可以减小过拟合的问题。
4. L2正则化
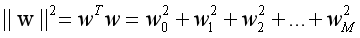
w0 通常从正则化中省略， 因为包含w0 会使得结果依赖于目标变量原点的选择。w0 也可以包含在正则化中，但是必须有自己的正则化系数。
5. L2正则化的含义之总结
L2正则化的含义，选择具有较小的值的w*,因为w*过大，则表明模型被过分的调参，过分的拟合了训练集，甚至拟合了训练集中的随机噪声，因此导致模型的过拟合。