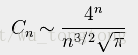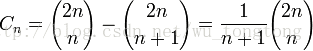卡特兰数

卡特兰数

关于卡特兰数

• 卡特兰数是一种经典的组合数，经常出现在各种计算中，其前几项为 :

1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

计算公式

• 常用计算公式：

[C_n=frac 1{n+1} binom {2n}{n}=frac {(2n)!}{(n+1)!n!} ]

• 有趣的另类递推式：

[C_n=C_{n-1} imes (4 imes n-2)/(n+1) ]

某些性质

• 据说(C_n)的另一种形式为$$C_n= binom {2n}{n}- binom{2n}{n-1}$$
• 所以，(C_n)是一个自然数，这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。卡特兰数满足以下递推关系$$C_0=1 quad and quad C_{n+1}=frac {2(2n+1)}{n+2}C_n$$
  也满足$$C_0=1 quad and quad C_{n+1}=sum_{i=0}^nC_iC_{i-1},ngeq 0$$
  这提供了一个更快速的方法来计算卡塔兰数。
  卡塔兰数的渐近增长为
  
  它的含义是左式除以右式的商趋向于1当n→∞（这可以用n!的斯特灵公式来证明。）
• 所有的奇卡塔兰数Cn都满足(n = 2^k − 1)。
• 所有其他的卡塔兰数都是偶数。

应用貌似hin广泛

• 从网上找一个经典问题：给出一个n，要求一个长度为2n的01序列，使得序列的任意前缀中1的个数不少于0的个数，以下为长度为6的序列:

[111000 101100 101010 110010 110100 ]

有好多情况

• 证明：

  • 令1表示进栈，0表示出栈，则可转化为求一个2n位，含n个1，n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数$$ binom {2n}{n}$$ 显然含n个1，n个0的2n位二进制数共有个，下面考虑不满足要求的数目。
    考虑一个含n个1，n个0的2n位二进制数，扫描到第(2m+1)位上时有(m+1)个0和m个1（容易证明一定存在这样的情况），
    则后面的01排列中必有(n-m)个1和(n-m-1)个0
    将2m+2及其以后的部分0变成1，1变成0，则对应一个(n+1)个0和)n-1)个1的二进制数
    反之亦然（相似的思路证明两者一一对应）
    从而
    
    将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数

  • (C_n)表示有n+1个叶子的二叉树的个数
    

  • (C_n)所有不同构的含n个分枝结点的满二叉树的个数（一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树）
                

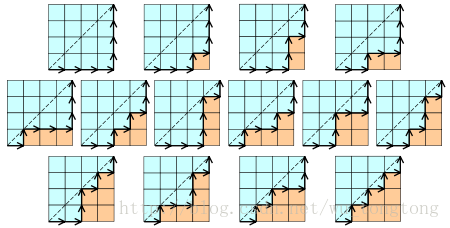
  • (C_n)表示所有在n × n格点中不越过对角线的单调路径的个数
    一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右
    计算这种路径的个数等价于计算Dyck word的个数：X代表“向右”，Y代表“向上”
    

  • Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数
    下图中为n = 4的情况：
    

  • Cn表示对{1, …, n}依序进出栈的置换个数
    一个置换w是依序进出栈的当S(w) = (1, …, n),
    其中S(w)递归定义如下：令w = unv，其中n为w的最大元素，u和v为更短的数列
    再令S(w) =S(u)S(v)n，其中S为所有含一个元素的数列的单位元。

  • Cn表示集合{1, …, n}的不交叉划分的个数. 其中每个段落的长度为2

  • Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数
    下图为 n = 4的情况: