算法的复杂度--[转]

一、算法的时间复杂度

1、概述

  算法的时间复杂度使用大O表示法，如O(1)、O(n)、O(logn)、O(n²)、O(n³)、O(2ⁿ)、O(n!)、O(√n)等，分别可以称为常数阶、线性阶、对数阶、平方阶、立方阶、指数阶、阶乘阶、平方根阶。

  推导大O阶可以遵循以下规则：
   ①. 用常数1来取代运行时间中所有加法常数。
   ②. 修改后的运行次数函数中，只保留最高阶项。
   ③. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。

2、常见时间复杂度

  ①、常数阶

  如下算法的运行的次数的函数为f(n)=3，根据推导大O阶的规则1，我们需要将常数3改为1，则这个算法的时间复杂度为O(1)，即常数阶。

void test()
{
    int sum = 0, x = 100; //执行一次  
    sum = (1 + x)*x / 2; //执行一次  
    System.out.println(sum); //执行一次 
}

  当算法的执行时间不随着输入大小n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数，所以其算法的时间复杂度是常数阶，即O(1)。

void func()
{
    int x = 90, y = 100;
    while (y > 0)
    {
        if (y >= 0)
        {
            x = x - 10;
            y--;
        }
    }
}

  ②、线性阶

  线性阶的代表有一重循环，随着输入n的增大，算法执行时间线性增长。比如下面的算法，在循环体中的代码执行了n次，因此时间复杂度为O(n)。

void func(int n)
{
    for (int i = 0; i<n; i++)
    {
        //时间复杂度为O(1)的算法
        ...
    }
}

  以下是求阶乘算法，可以看到n没增加1就多执行一次递归，所以其时间复杂度是线性的O(n)。

long long Fact(unsigned int n)
{
    if (n == 0)
        return 1;
    return n * Fact(n - 1);
}

   ③、对数阶

  如下代码，number初始值为1，并以每次乘2的变化越来越接近n，假设循环执行的次数为x，则由2^x = n可以得出x = log₂n，所以这个算法的时间复杂度为O(logn)，类似的二分法查找算法的时间复杂度也是O(logn)。

void func(int n)
{
    int number = 1;
    while (number < n) 
    {
        number = number * 2;
        //时间复杂度为O(1)的算法
        ...
    }
}

  ④、平方阶

  如下两层的嵌套循环的时间复杂度即为O(n²)：

for (int i = 0; i < n; i++)
{
    for (int j = 0; j < n; j++)
    {
        //时间复杂度为O(1)的算法
        ...
    }
}

  又如下面的冒泡排序算法，内循环中代码执行的次数为：n²/2 - n/2，推导大O阶的规则的第二条：只保留最高阶，因此保留n²/2，再根据第三条去掉和这个项的常数，即去掉1/2，所以冒泡算法的时间复杂度为O(n²)。

void BubbleSort(int ary[], unsigned int n)
{
    for (unsigned int i = 1; i < n; i++)
    {
        for (unsigned int j = i; j < n; j++)
        {
            if (ary[j] < ary[i - 1])
            {
                int temp = ary[i - 1];
                ary[i - 1] = ary[j];
                ary[j] = temp;
            }
        }
    }
}

  ⑤、立方阶

  如下所示的三层嵌套循环的时间复杂度为O(n³)：

for (int i = 0; i < n; i++)
{
    for (int j = 0; j < n; j++)
    {
        for (int k = 0; k < n; k++)
        {
            //时间复杂度为O(1)的算法
            ...
        }
    }
}

  3、时间复杂度与效率

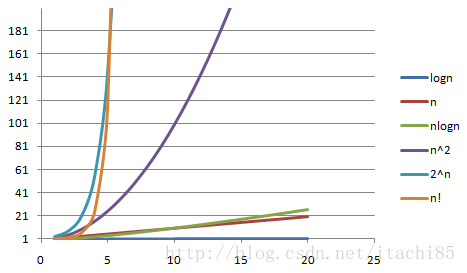
  O(logn)、O(n)、O(nlogn )随着n的增加，复杂度提升不大，因此这些复杂度属于效率高的算法，而O(2ⁿ)和O(n!)当n增加到50时，复杂度就突破十位数了，这种效率极差的复杂度最好不要出现在程序中。

  常用的时间复杂度按照耗费的时间从小到大依次是：O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!)，下面是一个更加直观的图： 

  

  二、算法的空间复杂度

  算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。

  类似时间复杂度，若算法执行时所需要的存储空间相对于输入n而言是一个常数，则算法的空间复杂度为O(1)。如下算法要分配的空间有n，j，i，k，即f(n) = 4，4为常数，所以空间复杂度是O(1)。

void func(int n)
{
    int j = 100;
    for (int i = 0; i < n; i++)
    {
        int k = i * k;
    }
}

  若一个算法是递归算法，由于递归需要压栈，所以其分配的空间为一次调用所分配的临时存储空间的大小乘以被调用的次数，所以递归算法的空间复杂度为1 + 递归调用的次数。比如下面的二分法查找算法的递归方式的空间复杂度为O(logn)：

 

int HalfFindValue(int ary[], const int& value, int low, int high)
{
    if (low > high) //未找到
        return -1;

    int mid = (low + high) / 2;
    if (ary[mid] == value)
        return mid;
    else if (ary[mid] > value)
        return HalfFindValue(ary, value, low, mid - 1);
    else
        return HalfFindValue(ary, value, mid + 1, high);
}

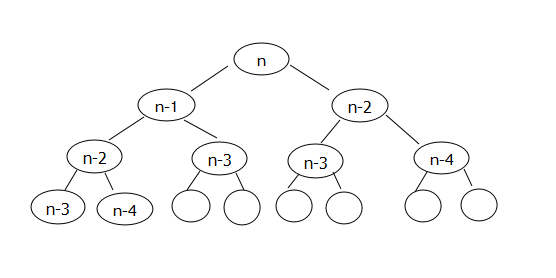
  对于斐波那契数列，如果按照下面普通的递归算法，根据图示，递归进入的次数与二叉树的结点个数相同，二叉树的深度为n，假设为满二叉树的话其结点个数为2ⁿ - 1，故其时间复杂度为O(2ⁿ)。而其空间复杂度可以看出与二叉树的深度相关，所以为O(n)。

  

long long Fib(int n)
{
    if (n <= 1)
        return 1;
    else
        return Fib(n - 1) + Fib(n - 2);
}

  由上可知，对于斐波那契数列使用递归算法求解的话其时间复杂度是效率极低的，它做了很多重复性的操作，可以使用下列的for循环代替它，使时间复杂度降低为O(n)：

long long Fibonacci(unsigned n)
{
    if (n <= 1)
        return 1;

    long long llOne = 0;
    long long llTwo = 1;
    long long llFib = 0;
    for (unsigned int i = 2; i <= n; ++i)
    {
        llFib = llOne + llTwo;
        llOne = llTwo;
        llTwo = llFib;
    }

    return llFib;
}

 

 以上转载和参考自：CSDN刘望舒的专栏：算法（一）时间复杂度，地址：https://blog.csdn.net/itachi85/article/details/54882603。