[Atcoder] AtCoder Beginner Contest 236 G Good Vertices

题意：

给一个有向图，每条边按照顺序一条一条往里面加。问对于每个点$i$，最早在第几条边加入的时候，存在一条$1$到$i$，长度为$L$的路径。不存在输出$-1$。

$n \le 100, m \le n^2$

$L \le 10^9$

解答：

$L\le 10^9$比较容易想到矩阵运算。

一个比较naive的想法是：对于每条边加入后，求邻接矩阵的$L$次幂，这样就知道哪些点可以从1号点经过$L$条边到达，暴力算就行，时间复杂度为$O(n^5logL)$。

然而看着正解，发现虽然是矩阵快速幂，但是和我上面这个想法差距有点大。

我们把原问题转化为：一开始加入所有边，但是第$i$条边的边权是$i$，那么对于每个点的答案就是求从$1$号点，到$i$号点，经过$L$条边的路径中最大边权最小是多少。

我们设$dp[i][u]$表示经过$i$条边到达$u$号节点，经过路径中最大边权最小是多少。

显然可以得到以下这个转移$dp[i][v] = min_{(u,v)\in g}{max{f[i - 1][u], g[u][v]}}$

我们可以用矩乘优化这个操作，我们设min为+，max为×。

那么

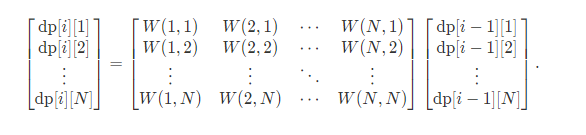
（图来自官网）

我们只要设$dp[0][1] = 0, dp[0][i] = inf$。这样答案就是后矩乘后的第一列。

代码很好写，但是为什么把加法和乘法定义成min,max，从而适用矩阵，官方题解中给出了解释。

一个运算可以使用矩阵优化，必须要他的乘法满足交换幺半群，加法满足幺半群。

并且乘法对加法有左右分配率。

幺半群就是存在e使得(A + e) = A的，满足结合律的代数系统。

交换幺半群是满足交换律的幺半群。

而分配率这个很容易搞。

想要记住这个结论，可以画3个二阶矩阵乘起来的展开式，分别对12,23加括号得到的式子，看看必须满足什么性质。

代码：

//
// Created by onglu on 2022/3/22.
//

#include <bits/stdc++.h>

#define all(a) a.begin(),a.end()
#define rall(a) a.rbegin(),a.rend()
#define endl '\n'
#define lson (rt << 1)
#define rson (rt << 1 | 1)
#define Mid ((l + r) / 2)
//#define int long long
using namespace std;
const int N = 2e6 + 1009;
//const int N = 2e5 + 1009;
//const int N = 5009;
//const int N = 309
int n, m;
int l;
struct mat {
    int n;
    int g[109][109];
};
mat operator*(const mat &a, const mat &b) {
    mat c;
    int n = a.n;
    c.n = a.n;
    for(int i = 1; i <= n; i++) {
        memset(c.g[i], 0x3f, sizeof(int) * (c.n + 5));
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            for(int k = 1; k <= n; k++) {
                c.g[i][j] = min(c.g[i][j], max(a.g[i][k], b.g[k][j]));
            }
        }
    }
    return c;
}
mat Pow(mat &a, int p) {
    mat ans;
    int f = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            ans.g[i][j] = 0x3f3f3f3f;
        }
        ans.g[i][i] = 0;
    }
    for( ; p; p = p >> 1, a = a * a) {
        if(p & 1) {
            ans = a * ans;
        }
    }
    return ans;
}
void work() {
    mat a;
    cin >> n >> m >> l;
    a.n = n;
    memset(a.g, 0x3f, sizeof(a.g));

    for(int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        a.g[y][x] = min(a.g[y][x], i);
    }
    a = Pow(a, l);
    for(int i = 1; i <= n; i++) {
        if(a.g[i][1] == 0x3f3f3f3f) {
            cout << -1 << " " ;
        } else {
            cout << a.g[i][1] << " ";
        }
    }
    cout << endl;
}

signed main() {
#ifdef LOCAL
    freopen("C:\\Users\\onglu\\CLionProjects\\acm\\data.in", "r", stdin);
    freopen("C:\\Users\\onglu\\CLionProjects\\acm\\data.out", "w", stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    int Case = 1;
//  cin >> Case;
    while (Case--) work();
    return 0;
}