讨论的是函数为一元的单值函数

1.黄金分割法

期望按照比例压缩查找区间,逼近极小点:
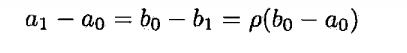


按照这类比例压缩,不断取值比较左右点大小,缩小区间范围,直到逼近。
2.斐波那契数列:和黄金分割类似,只是比例按照斐波那契数列的规则压缩区间
3.二分法:和黄金分割类似,只是比例按0.5二分压缩。
4.牛顿法
1)泰勒展开,构造对 f(x) 的近似 q(x)

2)迭代形式:转为求q(x)的极小点/导数为0

3)求解函数:可以逼近导数为0,也可以之间求解为个f '(x)=g(x)=0的函数等式

5.割线法
取两点,构造对牛顿法的近似,避免的二阶导可能不存在的情况

几何解释:

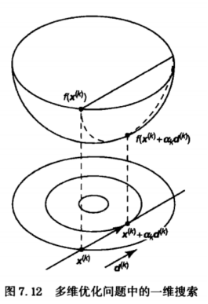
6.多元中的一元优化
一般迭代形式:由初始点x(k),步长ak,搜索方向d(x),迭代到x(k+1);对于ak:可由上面的黄金分割、二分等一维搜索方法找到最佳步长;方向d一般是梯度等方向。
![]()