第四章 特征值与特征向量

§4.1  特征值与特征向量

§4.1.1特征值与特征向量的概念及其计算

定义1.  设A是数域P上的一个n阶矩阵，l是一个未知量，

     

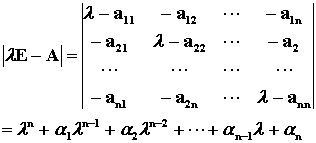
称为A的特征多项式，记 ¦(l)=| lE-A|，是一个P上的关于 l

的n次多项式，E是单位矩阵。

¦(l)=| lE-A|=lⁿ+a₁l^n-1+…+a_n= 0是一个n次代数方程，称为A的特征方程。 特征方程 ¦(l)=| lE-A|=0的根 (如：l₀) 称为A的特征根(或特征值)。 n次代数方程在复数域内有且仅有n 个根，而在实数域内不一定有根，因此特征根的多少和有无，不仅与A有关，与数域P也有关。

以A的特征值 l₀代入 (lE-A)X=0，得方程组 (l₀E-A)X=q，是一个齐次方程组，称为A的关于l₀的特征方程组。因为 |l₀E-A|=0，(l₀E-A)X=0 必存在非零解X⁽⁰⁾ ，X⁽⁰⁾ 称为A的属于 l₀的特征向量。所有l₀的特征向量全体构成了l₀的特征向量空间。

 

 

一. 特征值与特征向量的求法

    对于矩阵A，由AX=l₀X，l₀EX=AX，得：

         [l₀E-A]X=q  即齐次线性方程组

    

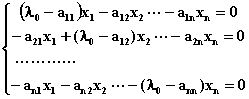
有非零解的充分必要条件是：

 

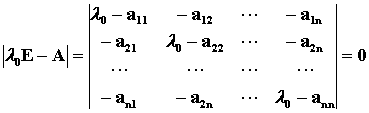
即说明特征根  是特征多项式 |l₀E-A| =0的根，由代数基本定理

 

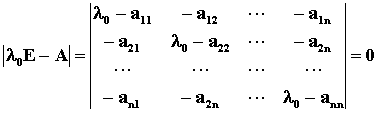
有n个复根 l₁, l₂,…, l_n，为A的n个特征根。

当特征根 l_i (I=1,2,…,n)求出后，(l_iE-A)X=q 是齐次方程，l_i均会使 |l_iE-A|=0，(l_iE-A)X=0 必存在非零解，且有无穷个解向量，(l_iE-A)X=0 的基础解系以及基础解系的线性组合都是A的特征向量。

例1. 求矩阵  的特征值与特征向量。

解：由特征方程

 

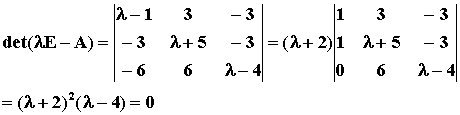
解得A有2重特征值 l₁=l₂=-2，有单特征值 l₃=4

对于特征值 l₁=l₂=-2，解方程组 (-2E-A)x=0

 

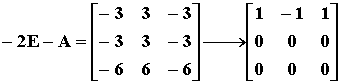
得同解方程组 x₁-x₂+x₃=0

解为x₁=x₂-x₃ (x₂,x₃为自由未知量)

分别令自由未知量 

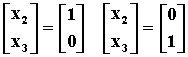
得基础解系 

所以A的对应于特征值 l₁=l₂=-2的全部特征向量为

x=k₁x₁+k₂x₂    (k₁,k₂不全为零)

可见，特征值 l=-2的特征向量空间是二维的。注意，特征值在重根时，特征向量空间的维数£特征根的重数。

对于特征值 l₃=4，方程组  (4E-A)x=0

 

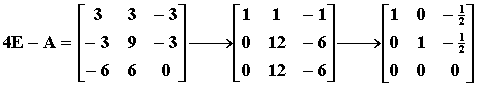
得同解方程组为 

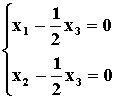
通解为 

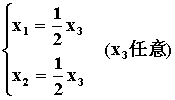
令自由未知量 x₃=2 得基础解系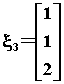  

所以A的对于特征值 l₃=4 得全部特征向量为 x= k₃ x₃

 

例2.       求矩阵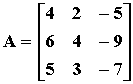  

的特征值与特征向量

解：由特征方程

 

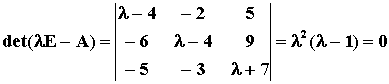
解得A有单特征值 l₁=1，有2重特征值 l₂=l₃=0

对于 l₁=1，解方程组 (E-A) x = 0

 

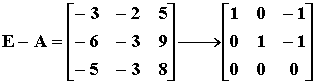
得同解方程组为 

同解为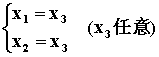 

令自由未知量 x₃=1，得基础解系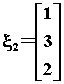 

所以A的对应于特征值 l₁=1的全部特征向量为 x=k₁x₁  (k₁¹0)

对于特征值 l₂=l₃=0，解方程组  (0E-A)=0

 

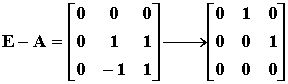
得同解方程组为 

通解为 

令自由未知量 x₃=1，得基础解系 

此处，二重根 l=0 的特征向量空间是一维的，特征向量空间的维数<特征根的重数，这种情况下，矩阵A是亏损的。

所以A的对应于特征值 l₂=l₃=0 得全部特征向量为 x=k₂x₃ 

 

例3．   矩阵  的特征值与特征向量

解：由特征方程

解得A的特征值为  l₁=1, l₂=i, l₃=-i

      对于特征值 l₁=1，解方程组 (E-A)=0 ，由

      

得通解为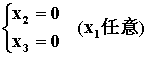

令自由未知量 x₁=1，得基础解系 x₁=(1,0,0)^T，所以A的对应于特征值 l₁=1得全部特征向量为 x=k₁x₁

      对于特征值 l₂=i，解方程组 (iE-A)=0

 

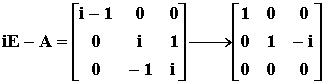
得同解方程组为

 

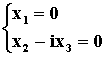
通解为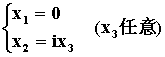

令自由未知量 x₃=1，得基础解系 x₂=(0,i,1)^T，所以A对应于特征值l₂=1的全部特征向量为 x=k₂x₂  (k₂¹0)。

      对于特征值 l₃=-i，解方程组 (-E-A)x=0，由

      

得同解方程组为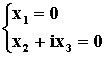

通解为

 

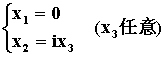
令自由未知量 x₃=1，，得基础解系 x₃=(0,-i,1)^T，所以A的对应于 l₃=-i的全部特征向量为 x=k₃x₃ 。特征根为复数时，特征向量的分量也有复数出现。

特征向量只能属于一个特征值。而特征值 l_i的特征向量却有无穷多个，他们都是齐次线性方程组 (l_iE-A)x=0 的非0解。其中，方程组(l_iE-A)x=0的基础解系就是属于特征值l_i的线性无关的特征向量。

 

性质1.  n阶方阵A=(a_ij)的所有特征根为l₁，l₂，…, l_n(包括重根)，则

   

证第二个式子：

由伟达定理，l₁l₂…l_n=(-1)ⁿa_n

又 |lE-A|=lⁿ+a₁l^{n -1}+…+a_n-1l₁+a_n 中用 l=0 代入二边，得：

|-A|=a_n， 而 |A|=(-1)ⁿa_n= l₁l₂…l_n，

 

性质2. 若 l 是可逆阵A的一个特征根，x为对应的特征向量，则

 是A^-1的一个特征根，x仍为对应的特征向量。

  证：

可见  是A^-1的一个特征根。

其中 l¹0，这是因为0不会为可逆阵的特征根，不然，若l_i=0,

|A|= l₁l₂…l_n=0，A奇异，与A可逆矛盾。

 

性质3. 若 l 是方阵A的一个特征根，x为对应的特征向量，则

l^m是A^m的一个特征根，x仍为对应的特征向量。

证：1) Ax=lx，二边左乘A，得：A²x=Alx=lAx=llx=l²x，

可见 l² 是 A² 的特征根；

    2) 若 l^m 是 A^m 的一个特征根，A^mx= l^mx，

   二边左乘A，得：A^m+1x=AA^mx=Al^mx=l^mAx=l^mlx=l^m+1x，

   得l^m+1是A^m+1的特征根

  用归纳法证明了l^m 是 A^m 的一个特征根。

 

性质4. 设 l₁，l₂，…, l_m是方阵A的互不相同的特征值。x_j是属于l_i 的特征向量( i=1,2,…,m)，则 x₁,x₂,…,x_m线性无关，即不相同特征值的特征向量线性无关 。

性质4给出了属于不相同特征值的特征向量之间的关系，因而是一个很重要的结论。

    性质4可推广为：设 l₁，l₂，…, l_m为方阵A的互不相同的特征值，x₁₁,x₁₂,…,x_1,k1是属于l₁的线性无关特征向量，……，x_m1,x_m2,…,x_m,k1是属于l_m 的线性无关特征向量。则向量组 x₁₁,x₁₂,…,x_1,k1,…, x_m1,x_m2,…,x_m,k1也是线性无关的。即对于互不相同特征值，取他们各自的线性无关的特征向量，则把这些特征向量合在一起的向量组仍是线性无关的。