$ color{#0066ff}{ 题目描述 }$
Welcome to SAO ( Strange and Abnormal Online)。这是一个 VR MMORPG, 含有 n 个关卡。但是,挑战不同关卡的顺序是一个很大的问题。
有 n – 1 个对于挑战关卡的限制,诸如第 i 个关卡必须在第 j 个关卡前挑战, 或者完成了第 k 个关卡才能挑战第 l 个关卡。并且,如果不考虑限制的方向性, 那么在这 n – 1 个限制的情况下,任何两个关卡都存在某种程度的关联性。即, 我们不能把所有关卡分成两个非空且不相交的子集,使得这两个子集之间没有任 何限制。
(color{#0066ff}{输入格式})
第一行,一个整数 T,表示数据组数。
对于每组数据,第一行一个整数 n,表示关卡数。接下来 n – 1 行,每行为 “i sign j”,其中 0 ≤ i, j ≤ n – 1 且 i ≠ j,sign 为“<”或者“>”,表示第 i 个关卡 必须在第 j 个关卡前/后完成。
(color{#0066ff}{输出格式})
对于每个数据,输出一行一个整数,为攻克关卡的顺序方案个数,mod 1,000,000,007 输出。
(color{#0066ff}{输入样例})
2
5
0 < 2
1 < 2
2 < 3
2 < 4
4
0 < 1
0 < 2
0 < 3
(color{#0066ff}{输出样例})
4
6
(color{#0066ff}{数据范围与提示})
对于 20%的数据有 n ≤ 10。
对于 40%的数据有 n ≤ 100。
对于另外 20%的数据有,保证数据中 sign 只会是<,并且 i < j。
对于 100%的数据有 T ≤ 5,1 ≤ n ≤ 1000。
(color{#0066ff}{题解})
题意就是给你个树形图,然后让你求拓扑序的数量
可以把它当做一棵树考虑, 然后再考虑边的限制
按照一般套路,我们会设(f[i])为以i为根子树的拓扑序的方案数, 然而这样我们并不能获得这个序列的形态,
而我们需要这些东西,具体来说,在DP的时候,我们需要具体知道点在拓扑序中的位置
比如x的孩子y,现在要让y与x合并,也就是说,把y的序列一个一个加进x,最终合并为长度(siz[x] +siz[y])的序列
但是还要保证x与y的位置关系,所以我们需要知道位置
于是加一维(f[i][j])表示以i为根子树,i在拓扑序中排在j的位置的子树方案数
难点其实在转移,即合并(f[x][p_1]和f[y][p_2]合并到f[x][p_3]),假设(p_1< p_2),x当前在(p_1),合并之后在(p_3),y当前在(p_2),合并之后再(p_4),如下图
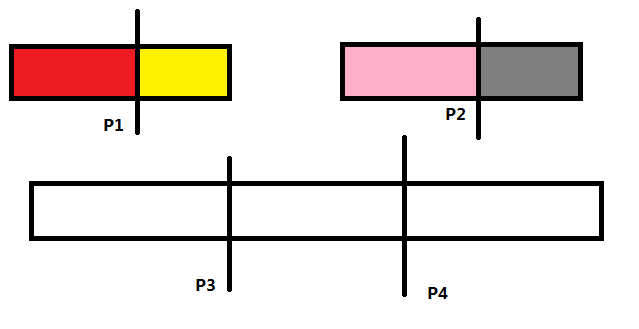
因为我们是把y的序列一个 一个往x的序列里插,所以红色部分肯定在(p_3)左边,黄色部分肯定在(p_3)右边
然后,灰色部分,肯定是在(p_4(p_4>p_3))右边的,但是粉色部分可以在(p_3)左边!
所以我们找一下(p_3)的范围,如果粉色全在(p_3)右边,那么就是(p_1),如果全在(p_3)左边,就是(p_1+p_2-1)
因此,(p_1le p3le p_1+p_2-1)
然后肯定是要组合一下的
(p_3)前面有红色部分,于是(C_{p_3-1}^{p_1-1})
(p_3)后面有黄色部分,于是(C_{siz[x]+siz[y]-p_3}^{siz[x]-p_1})
于是(f[x][p3]+=C_{p3−1}^{p1−1}C_{sizx+sizy−p3}^{sizx−p1}f[x][p1]f[y][p2])
注意f的值被更新了,DP的时候会乱,要开一个数组记一下原来的DP值
枚举时,我们可以这样
for(int p1 = 1; p1 <= siz[x]; p1++)
for(int p2 = 1; p2 <= siz[y]; p2++)
for(int p3 = p1; p3 <= p1 + p2 - 1; p3++)
DP转移
显然复杂度不太对。。
观察一下DP式子,发现只有一项有(p_2)!!!所以上一波前缀和,就行了
这个时候显然要把循环的第二行和第三行换个位置,就用上面(p_3)范围的式子,就能推出(p_2)的范围
for(int p1 = 1; p1 <= siz[x]; p1++)
for(int p3 = p1; p3 <= p1 + siz[y] - 1; p3++)
for(int p2 = p3 - p1 + 1; p2 <= siz[y]; p2++)
DP转移
这个是(p_1<p_2)的情况,反过来其实同理,推一下就行了,DP式子其实一样的,就是范围不一样
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
char getch() {
char ch = getchar();
while(ch != '<' && ch != '>') ch = getchar();
return ch;
}
const int mod = 1e9 + 7;
const int maxn = 2050;
struct node {
int to, dis;
node *nxt;
node(int to = 0, int dis = 0, node *nxt = NULL): to(to), dis(dis), nxt(nxt) {}
};
node *head[maxn];
int C[maxn][maxn], f[maxn][maxn], n, siz[maxn], g[maxn];
void predoit() {
for(int i = 0; i <= 1000; i++) {
C[i][0] = 1;
for(int j = 1; j <= i; j++)
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}
}
void add(int from, int to, int dis) { head[from] = new node(to, dis, head[from]); }
void init() {
for(int i = 1; i <= n; i++) {
head[i] = NULL;
for(int j = 0; j <= n; j++)
f[i][j] = 0;
}
}
void dp1(int x, int y) {
for(int i = 1; i <= n; i++) g[i] = f[x][i], f[x][i] = 0;
for(int p1 = 1; p1 <= siz[x]; p1++)
for(int p3 = p1; p3 <= p1 + siz[y] - 1; p3++)
(f[x][p3] += 1LL * C[p3 - 1][p1 - 1] * C[siz[x] + siz[y] - p3][siz[x] - p1] % mod
* g[p1] % mod * (f[y][siz[y]] - f[y][p3 - p1] + mod) % mod) %= mod;
}
void dp2(int x, int y) {
for(int i = 0; i <= n; i++) g[i] = f[x][i], f[x][i] = 0;
for(int p1 = 1; p1 <= siz[x]; p1++)
for(int p3 = p1 + 1; p3 <= p1 + siz[y]; p3++)
(f[x][p3] += 1LL * C[p3 - 1][p1 - 1] * C[siz[x] + siz[y] - p3][siz[x] - p1] % mod
* g[p1] % mod * f[y][p3 - p1] % mod) %= mod;
}
void dfs(int x, int fa) {
siz[x] = f[x][1] = 1;
for(node *i = head[x]; i; i = i->nxt) {
if(i->to == fa) continue;
dfs(i->to, x);
if(i->dis) dp1(x, i->to);
else dp2(x, i->to);
siz[x] += siz[i->to];
}
for(int i = 1; i <= siz[x]; i++) (f[x][i] += f[x][i - 1]) %= mod;
}
int main() {
predoit();
for(int T = in(); T --> 0;) {
n = in();
char p; int x, y; init();
for(int i = 1; i < n; i++) {
x = in() + 1, p = getch(), y = in() + 1;
add(x, y, p == '<'), add(y, x, p == '>');
}
dfs(1, 0);
printf("%d
", f[1][n]);
}
return 0;
}