并查集

转载于：https://zhuanlan.zhihu.com/p/213807228

并查集是什么

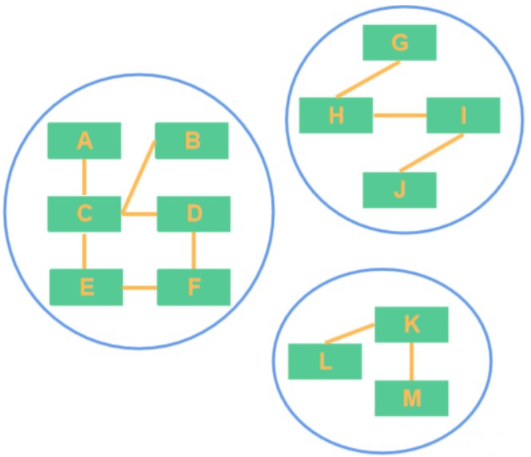
并查集，是一种判断“远房亲戚”的算法。

打个比方：你身边的某个“朋友”，很有可能就是你父亲的母亲的姑妈的大姨的哥哥的表妹的孙子的女儿的父亲的孙子。如果给定这么一张“家谱”（无向图），如何判断两个顶点是不是“亲戚”呢？用人话说，就是判断一个图中两个点是否联通（两个顶点相互联通则为亲戚）。

并查集是专门用来解决这样的问题的，和搜索不同，并查集在构建图的时候同时就标记出了哪个“人”属于哪个“团伙”（一团伙中的点两两联通）。

 

 并查集的操作

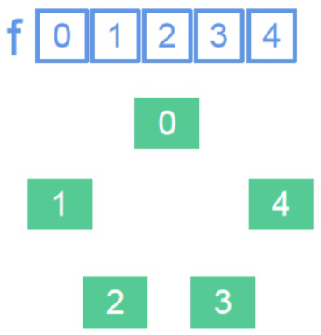
1. 初始化

并查集的思想是通过标记确定该顶点所在的组。

所以对于一个n个点，m条边的图，我们需要新建一个长度为n的数组f（可以理解为father），f[n]代表点n的团伙“代表人”，当两个点所在团伙“代表人”相同，则这两个点所在团伙相同。

而在最开始，每个顶点间都是互相不连通的，所以每个顶点单独属于一个团伙，每个顶点理所应当成为自己团伙的“代表人”，所以我们把f[n]的初始值赋为n。

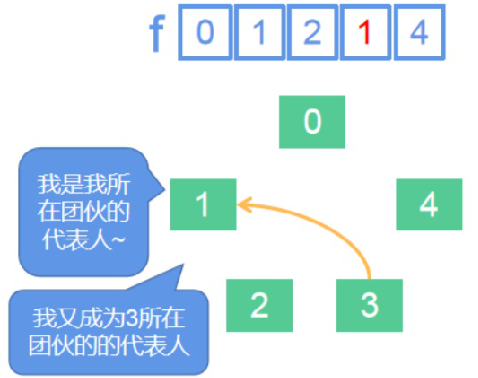
2. 合并团伙

我们以连接3和1这两个点做例子：

在连接点3和点1时，3和1形成了一个团伙，而3和1的团伙代表人f[3]和f[1]就应该统一，具体是让3做代表人还是让1做代表人随便，我们让1做代表人。f[3] = 1，这条语句可以理解为让1所在团伙的代表人同时成为3所在团伙的代表人。

 

(箭头只是体现了f数组中“团伙成员”和“代表人”的关系，其实这个图是无向图)

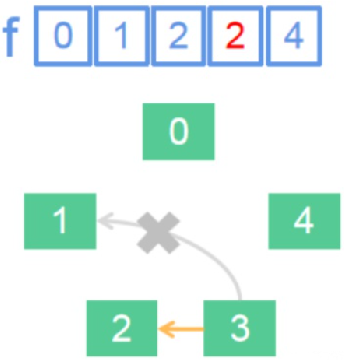
可是，像f[a] = b这样合并真的对吗？请读者考虑这样一种情况。

刚刚我们合并了3和1，现在我们需要合并3和2。如果按照f[a] = b这样合并，那么，f[3]就被赋值为了2。这样，f[3]原本的值1就被覆盖了，也就是说，1和3的团伙就被硬生生地“拆散”      了。  

 

下面我们换一个例子：合并3和4。此时我们不应该令f[3] =4，应该让f[3的团伙代表人] = (4的团伙代表人)，如下图。

 

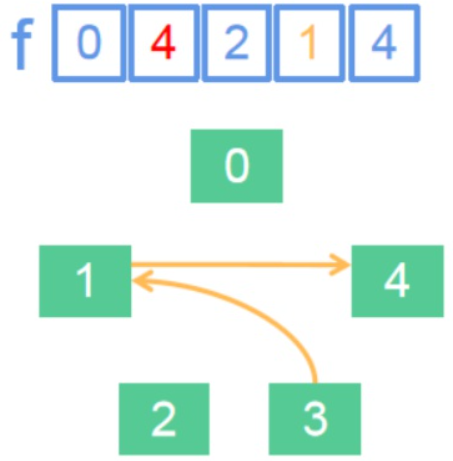
 这样，合并两个团伙的工作就完成了。总结起来就一句话：f[a的团伙代表人] = (b的团伙代表人)。

3. 查找团伙代表人

 紧接着，又一个问题浮出水面：根据上面的公式f[a的团伙代表人] = (b的团伙代表人)，可是a、b的团伙代表人怎么求？是f[a]吗？不不不，这里的情况变得复杂了。大家再次考虑一种特殊情况。

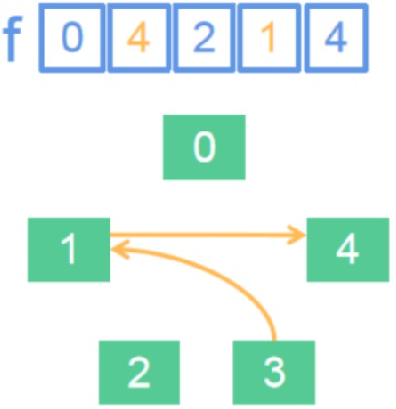
在这种情况下，3的团伙代表人是谁？1还是4？正确答案是4。因为，一个团伙中每一个点都直接或间接地“指向”这个团伙的代表人。（1,3,4）这个团伙中，1直接地指向4，3间接地指向4，所以4才是这个团伙里的代表人。

那么，点x的团伙代表人怎么求呢？我们会发现另一个特征，任何一个团伙的代表人a，都有f[a] = a。很好理解，团伙代表人也是团伙的一个成员，团伙代表人所在团伙的代表人就是它自己。

而对于其他点a，f[a]均不等于a。并且如果一个顶点a有f[a] ≠ a，那么这个点一定不是团伙的代表人，因为f[a]不会间接地或直接地指向a（并查集保证不会存在环）。

根据这一特性，我们可以判断点a是否为某个团伙的代表人。

在例子中，我们想要知道1是否为团伙代表人，就可以看f[1]是否等于1，很明显，f[1] = 4，所以1不是该团伙的代表人，我们要继续“追本溯源”，对5进行判断。这个过程就是一种递归的寻找过程。

知道了这个特性，我们就可以写出相应的C++代码（这里还给出了循环版的代码，根据情况使用）：

int getFather(int x) {
    return f[x] == x ? x : getFather(f[x]);
}

int getFather(int x) {
    while (f[x] != x)
        x = f[x];
    return x;
}

这是一个递归函数，如果f[x] = x，说明这个点已经是该团伙的代表人，直接返回就好了，如果它不是该团伙的代表人，那么就返回自己指向的点的团伙代表人。

在求getFather(3)时，f[3] != 3，返回getFather(f[3])也就是getFather(1)；

在求getFather(1)时，f[1] != 1，返回getFather(f[1])也就是getFather(4)；

在求getFather(4)时，f[4] == 4，返回4。递归结束。最后计算出3的团伙代表人是4。

4. 查询顶点是否在同一团伙

并查集的最后一种操作叫做查询，就是查询两个点是否连通（在同一团伙）。

前面已经讲了，当两个点所在团伙“代表人”相同，则这两个点所在团伙相同。判断两个点a、b在同一团伙的方法就是：

getFather(a) == getFather(b)

 5. 完整代码

const int N = 100; // 节点数量
int f[N];

int init() {
    // 初始化
    for (int i=0; i<N; i++)
        f[i] = i;
}

int getFather(int x) {
    // 查询所在团伙代表人
    return f[x]==x ? x : getFather(f[x]);
}

int merge(int a, int b) {
    // 合并操作
    f[getFather(a)] = getFather(b);
}

bool query(int a, int b) {
    // 查询操作
    return getFather(a) == getFather(b);
}

int main() {
    init();
    merge(3, 1); // 3和1是亲戚
    merge(1, 4); // 1和4是亲戚
    cout << getFather(3) << endl; // 输出3的团伙代表人+换行
    cout << query(3, 1) << endl; // 输出3和1是否是亲戚+换行
}

并查集巧妙吧！我们既没有构建图，也没有构建边，自始至终只用到了f数组，又优化了时间。

不要小瞧并查集代码短，在很多时候并查集都会派上用场，比如著名的克鲁斯卡尔算法，就是通过并查集判断两个顶点是否相连的。更重要的是体会并查集的思想，用这种思想来优化代码。

王道的讲解：