一、树与二叉树的性质
1、 答案:A

解析:D选项中,第 i 个结点的左孩子不一定存在。
2、答案:C
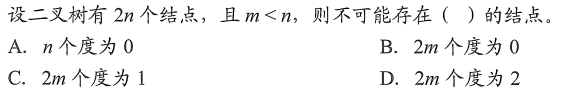
解析:
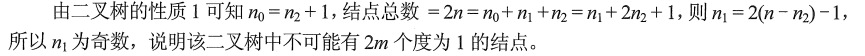
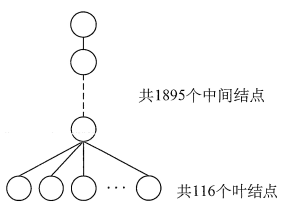
3、答案:D

解析:

二、二叉树的遍历和线索二叉树
1、若有一个叶子结点是二叉树中某个子树的中序遍历结果序列的最后一个结点,则它一定是该子树的前序遍历结果序列的最后一个结点。
2、答案:D

解析:C的反例
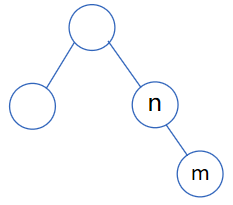
3、答案:C

解析: 因为后序遍历,无论是在左子树还是右子树,在返回的路上,都必然会经过祖先节点,所以,不管是不是递归的方法,都可以找得到这条路径。只要从栈中提出n,则栈里面剩下的就是从根节点到n的路径节点。
举例:(原文链接:https://blog.csdn.net/liuchuo/article/details/88413073)
首先需要理解的是,前中后序遍历都是通过递归的方式,将后来需要用到的结点保存在栈中,比如下面这颗树:
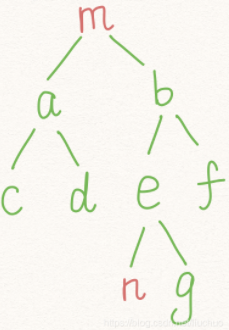
“如果是前序遍历,根左右,过程是:根节点m入栈并输出,访问m的左孩子a,a入栈并输出,访问a的左孩子c,c入栈并输出,c没有左孩子,无元素入栈,c没有右孩子,无元素入栈,c出栈,此时栈顶元素为a,访问a元素的右孩子d,d入栈并输出,d没有左孩子,无元素入栈,d没有右孩子,无元素入栈,d出栈,a左右子树都访问完了所以出栈,现在栈顶元素是m,m已经没有作用了所以出栈,访问m的右孩子b,m的右孩子b入栈并输出,接着访问b的左孩子e,e入栈并输出……
如果中序遍历,左根右,过程是:根节点m入栈,访问m的左孩子,所以m的左孩子a入栈,访问a的左孩子,所以a的左孩子c入栈,c没有左孩子,c现在输出并出栈,c没有右孩子所以没有元素入栈,现在栈顶元素是a,a输出并出栈,a的右孩子d入栈,此时d没有左孩子所以没有元素入栈,d输出并出栈,d没有右孩子所以没有元素入栈,现在栈顶元素是m,m输出,此时m已经没有作用了所以出栈,m的右孩子b入栈,访问b的左孩子,所以b的左孩子e入栈……
所以在前序和中序的过程中,如果n在m的右子树部分,遍历过程中找到了n,但是m已经不在栈中,因为栈中只会保留等会需要用到的e和b结点,而m已经完成了访问根结点和m的左子树的任务,已经被出栈,所以无法追溯n如何走到m。
但是后序遍历就不一样啦,后序的顺序是左右根,所以只要m的左右子树还没遍历完成,m就不能出栈,在遍历m的左右子树过程中,无论在m的左边还是右边找到了n,都可以直接返回然后根据栈中的路径让n找到回到m的路,这样就能找到m到n的路径~
所以一旦n在m的右子树,且离的较远,m就会在前序和中序的过程中因为已经完成了访问左、访问根的任务,而被栈遗忘,让找到了n的时候也不知怎么回到m……而只有后序会让作为祖先(子树的根)的m永远被铭记直到n找到m为止…”
4、答案:C

解析:因为前序和后序无法确定唯一的一颗二叉树,所以这种题的思路可以是用前序和答案每个选项的中序,画出二叉树,然后看此二叉树的后序符不符合题目要求。
5、答案:C

解析:

6、答案:C

解析:
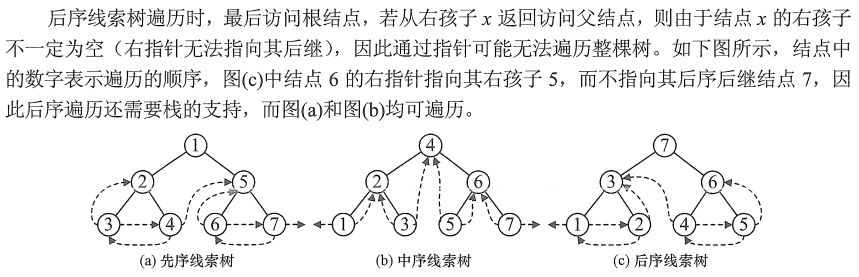
7、答案:B

解析:一棵二叉树的构建可以看作是一次入栈—出栈的过程。 (原文链接:https://www.cnblogs.com/Irvingcode/p/13356201.html)
对一个结点来说:
a. 当它在栈中时,往后入栈的元素都是它的左子树
b. 出栈之后,往后入栈的元素都是它的右子树
用递归的思想,这一次完整的将所有结点入栈—出栈的过程就能构造一棵唯一的二叉树。
举例说明:
(a入栈,b入栈,b出栈,c入栈,c出栈,a出栈,d入栈,d出栈)
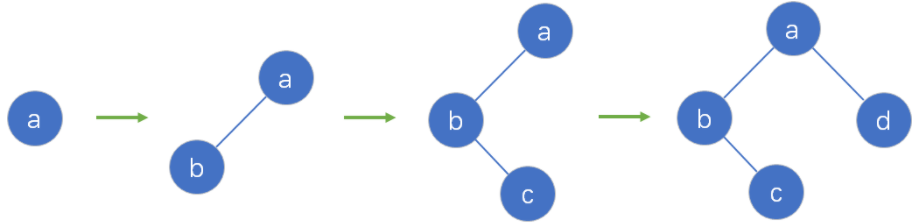
出栈顺序:b-c-a-d
出栈顺序 = 此二叉树的中序遍历
而前序+中序可以唯一确定一棵二叉树
所以,有多少种出栈的顺序,就有对应多少颗不同的二叉树了

三、树、森林
1、答案:D

解析:

2、答案:C

解析:

3、答案:D

解析:

4、答案:C

解析:

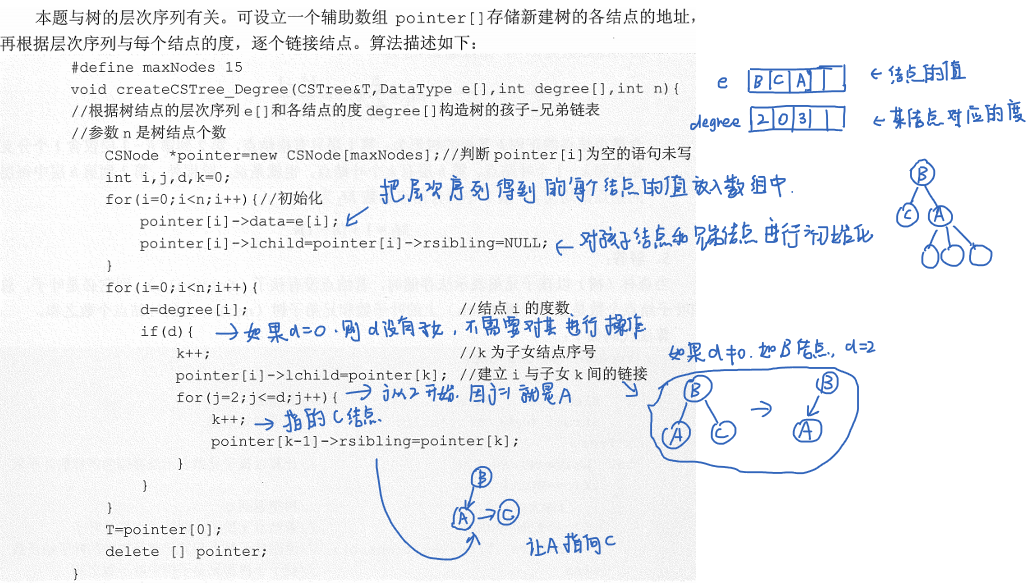
5、已知一棵树的层次序列及每个结点的度,编写算法构造此树的孩子-兄弟链表。
解析: