聚类分析
聚类分析和判别分析有相似的作用,都是起到分类的作用。但是,判别分析是已知分 类然后总结出判别规则,是一种有指导的学习;而聚类分析则是有了一批样本,不知道它们 的分类,甚至连分成几类也不知道,希望用某种方法把观测进行合理的分类,使得同一类的 观测比较接近,不同类的观测相差较多,这是无指导的学习。
所以,聚类分析依赖于对观测间的接近程度(距离)或相似程度的理解,定义不同的距离 量度和相似性量度就可以产生不同的聚类结果。
SAS/STAT中提供了谱系聚类、快速聚类、变量聚类等聚类过程。
谱系聚类方法介绍
谱系聚类是一种逐次合并类的方法,最后得到一个聚类的二叉树聚类图。其想法是, 对于 ![]() 个观测,先计算其两两的距离得到一个距离 矩阵,然后把离得最近的两个观测合并为一类,于是我们现在只剩了
个观测,先计算其两两的距离得到一个距离 矩阵,然后把离得最近的两个观测合并为一类,于是我们现在只剩了 ![]() 个类(每个单独的未合并的观测作为一个类 )。计算这
个类(每个单独的未合并的观测作为一个类 )。计算这 ![]() 个类两两之间的距离,找到离得最近的两个 类将其合并,就只剩下了
个类两两之间的距离,找到离得最近的两个 类将其合并,就只剩下了 ![]() 个类……直到剩下两个类,把它们合并为一 个类为止。当然,真的合并成一个类就失去了聚类的意义,所以上面的聚类过程应该在某个 类水平数(即未合并的类数)停下来,最终的类就取这些未合并的类。决定聚类个数是一个 很复杂的问题。
个类……直到剩下两个类,把它们合并为一 个类为止。当然,真的合并成一个类就失去了聚类的意义,所以上面的聚类过程应该在某个 类水平数(即未合并的类数)停下来,最终的类就取这些未合并的类。决定聚类个数是一个 很复杂的问题。
设观测个数为 ![]() ,变量个数为
,变量个数为 ![]() ,
, ![]() 为在某一聚类水平上的类的个数,
为在某一聚类水平上的类的个数, ![]() 为第
为第 ![]() 个观测,
个观测, ![]() 是当前(水平
是当前(水平 ![]() )的第
)的第 ![]() 类,
类, ![]() 为
为 ![]() 中的观测个数,
中的观测个数, ![]() 为均值向量,
为均值向量, ![]() 为类
为类 ![]() 中的均值向量(中心),
中的均值向量(中心), ![]() 为欧氏长度,
为欧氏长度,  为总离差平方和,
为总离差平方和, 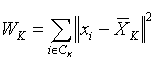 为类
为类 ![]() 的类内离差平方和,
的类内离差平方和, ![]() 为聚类水平
为聚类水平 ![]() 对应的各类的类内离差平方和的总和。假设 某一步聚类把类
对应的各类的类内离差平方和的总和。假设 某一步聚类把类 ![]() 和类
和类 ![]() 合并为下一水平的类
合并为下一水平的类![]() ,则定义
,则定义 ![]() 为合并导致的类内离差平方和的增量。用
为合并导致的类内离差平方和的增量。用 ![]() 代表两个观测之间的距离或非相似性测度,
代表两个观测之间的距离或非相似性测度, ![]() 为第
为第 ![]() 水平的类
水平的类 ![]() 和类
和类 ![]() 之间的距离或非相似性测度。
之间的距离或非相似性测度。
进行谱系聚类时,类间距离可以直接计算,也可以从上一聚类水平的距离递推得到。观测 间的距离可以用欧氏距离或欧氏距离的平方,如果用其它距离或非相似性测度得到了一个观 测间的距离矩阵也可以作为谱系聚类方法的输入。
根据类间距离的计算方法的不同,有多种不同的聚类方法。其中几种介绍如下:
一、类平均法(METHOD=AVERAGE)
测量两类每对观测间的平均距离,即
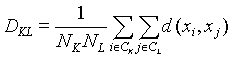
在 ![]() 时若类
时若类 ![]() 和类
和类 ![]() 合并为下一水平的类
合并为下一水平的类 ![]() 类,则类
类,则类 ![]() 和类
和类 ![]() 的距离的递推公式为
的距离的递推公式为
![]()
二、重心法(METHOD=CENTROID)
重心法测量两个类的重心(均值)之间的(平方)欧氏距离。即
![]()
当观测间距离为平方欧氏距离时有递推公式
![]()
三、最长距离法(METHOD=COMPLETE)
计算两类观测间最远一对的距离,即
![]()
递推公式为 ![]() 。
。
四、最短距离法(METHOD=SINGLE)
计算两类观测间最近一对的距离,即
![]()
递推公式为 ![]() 。
。
五、密度估计法(METHOD=DENSITY)
密度估计法按非参数密度来定义两点间的距离 ![]() 。如果两个点
。如果两个点 ![]() 和
和 ![]() 是近邻(两点距离小于某指定常数或
是近邻(两点距离小于某指定常数或 ![]() 在距离
在距离 ![]() 最近的若干点内)则距离是两点密度估计的 倒数的平均,否则距离为正无穷。密度估计有最近邻估计(K=)、均匀核估计(R=)和Wong 混合法(HYBRID)。
最近的若干点内)则距离是两点密度估计的 倒数的平均,否则距离为正无穷。密度估计有最近邻估计(K=)、均匀核估计(R=)和Wong 混合法(HYBRID)。
六、Ward最小方差法(或称Ward离差平方和法,METHOD=WARD)
![]()
当观测间距离为 ![]() 时递推公式为
时递推公式为
![]()
Ward方法并类时总是使得并类导致的类内离差平方和增量最小。
其它的聚类方法还有EML法、可变类平均法(FLEXIBLE)、McQuitty相似分析法(MCQUITTY )、中间距离法(MEDIAN)、两阶段密度估计法(TWOSTAGE)等。
谱系聚类类数的确定
谱系聚类最终得到一个聚类树,可以把所有观测聚为一类。到底应该把观测分为几类 是一个比较困难的问题,因为分类问题本身就是没有一定标准的,关于这一点《实用多元统 计分析》(王学仁、王松桂,上海科技出版社)第十章给出了一个很好的例子,即扑克牌的 分类。我们可以把扑克牌按花色分类,按大小点分类,按桥牌的高花色低花色分类,等等。
决定类数的一些方法来自统计的方差分析的思想,我们在这里作一些介绍。
一、 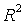 统计量
统计量
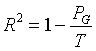
其中 ![]() 为分类数为
为分类数为 ![]() 个类时的总类内离差平方和,
个类时的总类内离差平方和, ![]() 为所有变量的总离差平方和。
为所有变量的总离差平方和。 ![]() 越大,说明分为
越大,说明分为 ![]() 个类时每个类内的离差平方和都比较小,也 就是分为
个类时每个类内的离差平方和都比较小,也 就是分为 ![]() 个类是合适的。但是,显然分类越多,每个 类越小,
个类是合适的。但是,显然分类越多,每个 类越小, ![]() 越大,所以我们只能取
越大,所以我们只能取 ![]() 使得
使得 ![]() 足够大,但
足够大,但 ![]() 本身比较小,而且
本身比较小,而且 ![]() 不再大幅度增加。
不再大幅度增加。
二、半偏相关
在把类 ![]() 和类
和类 ![]() 合并为下一水平的类
合并为下一水平的类 ![]() 时,定义半偏相关
时,定义半偏相关
半偏 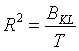
其中 ![]() 为合并类引起的类内离差平方和的增量,半 偏相关越大,说明这两个类越不应该合并,所以如果由
为合并类引起的类内离差平方和的增量,半 偏相关越大,说明这两个类越不应该合并,所以如果由 ![]() 类合并为
类合并为 ![]() 类时如果半偏相关很大就应该取
类时如果半偏相关很大就应该取 ![]() 类。
类。
三、双峰性系数
![]()
其中 ![]() 是偏度,
是偏度, ![]() 是峰度。大于0.555的
是峰度。大于0.555的 ![]() 值(这时为均匀分布)可能指示有双峰或多 峰边缘分布。最大值1.0(二值分布)从仅取两值的总体得到。
值(这时为均匀分布)可能指示有双峰或多 峰边缘分布。最大值1.0(二值分布)从仅取两值的总体得到。
四、伪F统计量

伪F统计量评价分为 ![]() 个类的效果。如果分为
个类的效果。如果分为 ![]() 个类合理,则类内离差平方和(分母)应该 较小,类间平方和(分子)相对较大。所以应该取伪F统计量较大而类数较小的聚类水平。
个类合理,则类内离差平方和(分母)应该 较小,类间平方和(分子)相对较大。所以应该取伪F统计量较大而类数较小的聚类水平。
五、伪  统计量
统计量
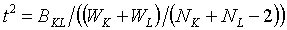
用此统计量评价合并类 ![]() 和类
和类 ![]() 的效果,该值大说明不应合并这两个类,所 以应该取合并前的水平。
的效果,该值大说明不应合并这两个类,所 以应该取合并前的水平。
用CLUSTER过程和TREE过程进行谱系聚类
一、CLUSTER过程用法
CLUSTER过程的一般格式为:
PROC CLUSTER DATA=输入数据集 METHOD=聚类方法 选项;
VAR 聚类用变量; COPY 复制变量; RUN;
其中的VAR语句指定用来聚类的变量。COPY语句把指定的变量复制到OUTTREE=的数据集中。 PROC CLUSTER语句的主要选项有:
- METHOD=选项,这是必须指定的,此选项决定我们要用的聚类方法,主要由类间距离定义 决定。方法有AVERAGE、CENTROID、COMPLETE、SINGLE、DENSITY、WARD、EML、FLEXIBLE、MCQUITTY 、MEDIAN、TWOSTAGE等,其中DENSITY、TWOSTAGE等方法还要额外指定密度估计方法(K=、R= 或HYBRID)。
- 输入DATA=数据集,可以是原始观测数据集,也可以是距离矩阵数据集。
- OUTTREE=输出谱系聚类树数据集,把谱系聚类树输出到一个数据集,可以用TREE过程绘 图并实际分类。
- STANDARD选项,把变量标准化为均值0,标准差1。
- PSEUDO选项和CCC选项。PSEUDO选项要求计算伪F和伪
 统计量,CCC选项要求计算
统计量,CCC选项要求计算 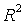 、半偏
、半偏 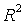
和CCC统计量。其中CCC统计量也是一种考察聚类效果的统计量,CCC较大的聚类水平是较好的 。
二、TREE过程用法
TREE过程可以把CLUSTER过程产生的OUTTREE=数据集作为输入,画出谱系聚类的树图,并 按照用户指定的聚类水平(类数)产生分类结果数据集。一般格式如下:
PROC TREE DATA=输入聚类结果数据集 OUT=输出数据集 GRAPHICS NCLUSTER=类数 选项; COPY 复制变量; RUN;
其中COPY语句把输入数据集中的变量复制到输出数据集(实际上这些变量也必须在CLUSTER 过程中用COPY语句复制到OUTTREE=数据集)。PROC TREE语句的重要选项有:
- DATA=数据集,指定从CLUSTER过程生成的OUTTREE=数据集作为输入。
- OUT=数据集,指定包含最后分类结果(每一个观测属于哪一类,用一个CLUSTER变量区 分)的输出数据集。
- NCLUSTERS=选项,由用户指定最后把样本观测分为多少个类。
- GRAPHICS,这是指定画谱系聚类的树图时使用高分辨率图形(要求有SAS/GRAPH模块)。
- HORIZONTAL,画树图时横向画。
三、例子
我们以多元分析中一个经典的数据作为例子,这是Fisher分析过的鸢尾花数据,有三 种不同鸢尾花(Setosa、Versicolor、Virginica),种类信息存入了变量SPECIES,并对每 一种测量了50棵植株的花瓣长(PETALLEN)、花瓣宽(PETALWID)、花萼长(SEPALLEN)、 花萼宽(SEPALWID)。这个数据已知分类,并不属于聚类分析的研究范围。这里我们为了示 例,假装不知道样本的分类情况(既不知道类数也不知道每一个观测属于的类别),让SAS取 进行聚类分析,如果得到的类数和分类结果符合真实的植物分类,我们就可以知道聚类分析 产生了好的结果。
这里我们假定数据已输入SASUSER.IRIS中(见系统帮助菜单的“Sample Programs | SAS/STAT | Documentation Example 3 from Proc Cluster”)。为了进行谱系聚类并产生帮助确定 类数的统计量,使用如下过程:
proc cluster data=sasuser.iris method=ward outtree=otree pseudo ccc; var petallen petalwid sepallen sepalwid; copy species; run;
可以显示如下的聚类过程(节略):
T
Pseudo Pseudo i
NCL -Clusters Joined- FREQ SPRSQ RSQ ERSQ CCC F t**2 e
149 OB16 OB76 2 0.000000 1.0000 . . . .
148 OB2 OB58 2 0.000007 1.0000 . . 1854.1 . T
147 OB96 OB107 2 0.000007 1.0000 . . 1400.1 . T
146 OB89 OB113 2 0.000007 1.0000 . . 1253.1 . T
145 OB65 OB126 2 0.000007 1.0000 . . 1182.9 . T
……………………………………
25 CL50 OB57 7 0.000634 0.9824 0.973335 6.446 291.0 5.6
24 CL78 CL62 7 0.000742 0.9817 0.972254 6.430 293.5 9.8
23 CL68 CL38 9 0.000805 0.9809 0.971101 6.404 296.0 6.9
22 CL30 OB137 6 0.000896 0.9800 0.969868 6.352 298.3 5.1
21 CL70 CL33 4 0.000976 0.9790 0.968545 6.290 300.7 3.2
20 CL36 OB25 10 0.001087 0.9779 0.967119 6.206 302.9 9.8
19 CL40 CL22 19 0.001141 0.9768 0.965579 6.146 306.1 7.7
18 CL25 CL39 10 0.001249 0.9755 0.963906 6.082 309.5 6.2
17 CL29 CL45 16 0.001351 0.9742 0.962081 6.026 313.5 8.2
16 CL34 CL32 15 0.001462 0.9727 0.960079 5.984 318.4 9.0
15 CL24 CL28 15 0.001641 0.9711 0.957871 5.929 323.7 9.8
14 CL21 CL53 7 0.001873 0.9692 0.955418 5.850 329.2 5.1
13 CL18 CL48 15 0.002271 0.9669 0.952670 5.690 333.8 8.9
12 CL16 CL23 24 0.002274 0.9647 0.949541 4.632 342.4 9.6
11 CL14 CL43 12 0.002500 0.9622 0.945886 4.675 353.3 5.8
10 CL26 CL20 22 0.002694 0.9595 0.941547 4.811 368.1 12.9
9 CL27 CL17 31 0.003060 0.9564 0.936296 5.018 386.6 17.8
8 CL35 CL15 23 0.003095 0.9533 0.929791 5.443 414.1 13.8
7 CL10 CL47 26 0.005811 0.9475 0.921496 5.426 430.1 19.1
6 CL8 CL13 38 0.006042 0.9414 0.910514 5.806 463.1 16.3
5 CL9 CL19 50 0.010532 0.9309 0.895232 5.817 488.5 43.2
4 CL12 CL11 36 0.017245 0.9137 0.872331 3.987 515.1 41.0
3 CL6 CL7 64 0.030051 0.8836 0.826664 4.329 558.1 57.2
2 CL4 CL3 100 0.111026 0.7726 0.696871 3.833 502.8 115.6
1 CL5 CL2 150 0.772595 0.0000 0.000000 0.000 . 502.8
伪F图形
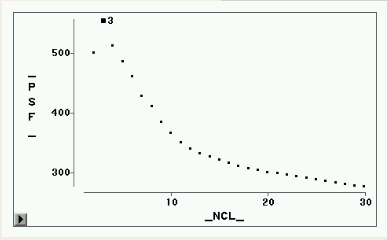
CCC图形
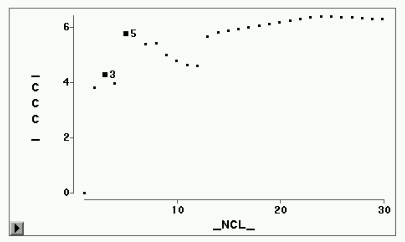
伪![]() 图形
图形
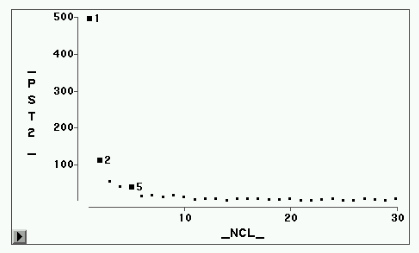
半偏![]() 图形
图形
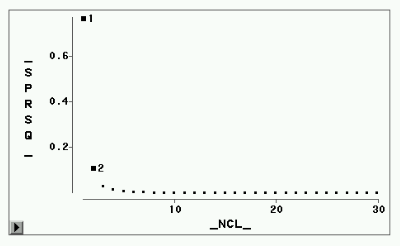
这个输出列出了把150个观测每次合并两类,共合并149次的过程。NCL列指定了聚类水平G (即这一步存在的单独的类数)。“-Clusters Joined-”为两列,指明这一步合并了哪两个 类。其中OBxxx表示哪一个原始观测,而CLxxx表示在哪一个聚类水平上产生的类。 比如,NCL为149时合并的是OB16和OB76,即16 号观测和76号观测,NCL为1(最后一次合并)合并的是CL5和CL2,即类水平为5时得到的类和 类水平为2时得到的类,CL5又是由CL9和CL19合并得到的,CL2是由CL4和CL3合并得到的,等 等。FREQ表示这次合并得到的类有多少个观测。SPRSQ是半偏 ![]() ,RSQ是
,RSQ是 ![]() ,ERSQ是在均匀零假设下的
,ERSQ是在均匀零假设下的 ![]() 的近似期望值,CCC为CCC统计量,Pseudo F 为伪F统计量,Pseudo t**2为伪
的近似期望值,CCC为CCC统计量,Pseudo F 为伪F统计量,Pseudo t**2为伪 ![]() 统计量,Norm RMS Dist是正规化的的两类 元素间距离的均方根,Tie指示距离最小的候选类对是否有多对。
统计量,Norm RMS Dist是正规化的的两类 元素间距离的均方根,Tie指示距离最小的候选类对是否有多对。
因为我们假装不知道数据的实际分类情况,所以我们必须找到一个合理的分类个数。 为此,考察CCC、伪F、伪 ![]() 和半偏
和半偏 ![]() 统计量。我们打开INSIGHT界面,调入上面 产生的OTREE数据集,绘制各统计量的图形。因为类水平太大时的信息没有多少用处,所以我 们对OTREE数据集取其类水平不超过30的观测,即:
统计量。我们打开INSIGHT界面,调入上面 产生的OTREE数据集,绘制各统计量的图形。因为类水平太大时的信息没有多少用处,所以我 们对OTREE数据集取其类水平不超过30的观测,即:
data ot; set otree; where _ncl_ <= 30; run;
各统计量的图形见图2-图5。CCC统计量建议取5类或3类(局部最大值),伪F建议3类( 局部最大值),伪 ![]() 建议3类(局部最大值处是不应合并的,即 局部最大值处的类数加1),半偏
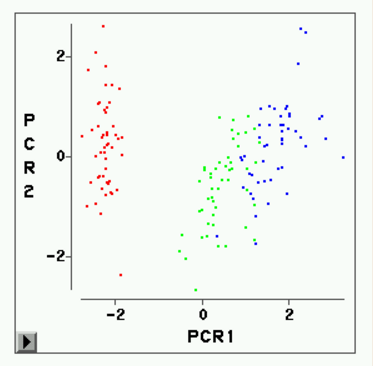
建议3类(局部最大值处是不应合并的,即 局部最大值处的类数加1),半偏 ![]() 建议3类。由这些指标看比较一致的是3类, 其次是5类。为了看为什么不能明显地分为三类,我们对四个变量求主分量,画出前两个主分 量的散点图(见图6)。可以看出Setosa(红色)与其它两类分得很开,而Versicolor(绿色 )与Virginica(蓝色)则不易分开。
建议3类。由这些指标看比较一致的是3类, 其次是5类。为了看为什么不能明显地分为三类,我们对四个变量求主分量,画出前两个主分 量的散点图(见图6)。可以看出Setosa(红色)与其它两类分得很开,而Versicolor(绿色 )与Virginica(蓝色)则不易分开。
因为我们知道要分成3类,所以我们用如下的TREE过程绘制树图并产生分类结果数据 集:
proc tree data=otree graphics horizontal nclusters=3 out=oclust; copy species; run;
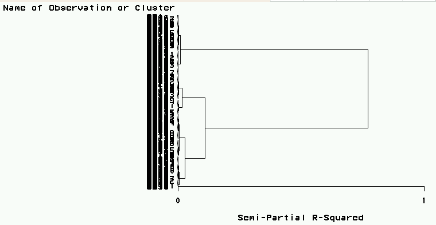
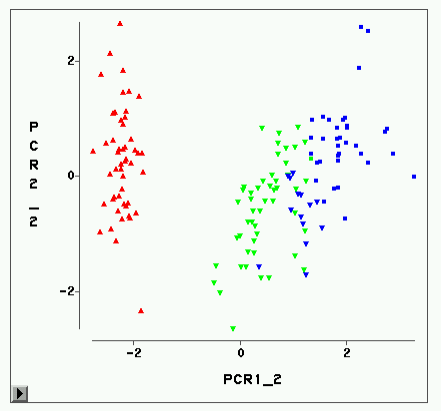
树图见图7,因为观测过多所以图显得杂乱。从图中也可以看出,分为两类可以分得很开 ,而分成三类时距离则不够远。如果上面的TREE过程去掉输出数据集要求,可以用包含最后 的聚类过程的OT数据集来作为输入。这个TREE过程用NCLUSTERS=3指定了分成3个类,结果数 据集OCLUST中有一个CLUSTER变量代表生成的分类。我们把这个数据集调入INSIGHT中用不同 颜色代表SPECIES(实际种类),用不同符号代表不同聚类过程分类,作前两个主分量散点图 (见图8)。可以看出,有Virsicolor和Virginica两类互相都有分错为对方的。
为了统计分类结果,可以用FREQ过程作表:
proc freq data=oclust;
tables species*cluster /
nopct norow nocol;
run;
得
SPECIES(Species) CLUSTER
Frequency | 1| 2| 3| Total
-----------+--------+--------+--------+
Setosa | 0 | 0 | 50 | 50
-----------+--------+--------+--------+
Versicolor | 49 | 1 | 0 | 50
-----------+--------+--------+--------+
Virginica | 15 | 35 | 0 | 50
-----------+--------+--------+--------+
Total 64 36 50 150
可见Virginica被分错的较多。
读者可以自己试用其它的类间距离来聚类,可以得到不同的结果。
(写的太好,摘抄于此, 原文链接“http://www.math.pku.edu.cn/teachers/lidf/docs/statsoft/html/sas-5/cluster.html”)