UVA10054-The Necklace（无向图欧拉回路——套圈算法）

Problem UVA10054-The Necklace

Time Limit: 3000 mSec

Problem Description

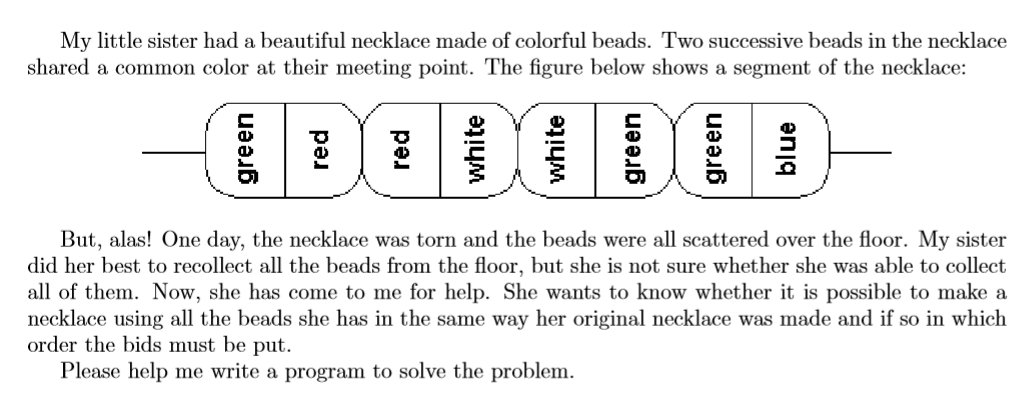
Input

The input contains T test cases. The first line of the input contains the integer T. The first line of each test case contains an integer N (5 ≤ N ≤ 1000) giving the number of beads my sister was able to collect. Each of the next N lines contains two integers describing the colors of a bead. Colors are represented by integers ranging from 1 to 50.

Output

For each test case in the input first output the test case number as shown in the sample output. Then if you apprehend that some beads may be lost just print the sentence “some beads may be lost” on a line by itself. Otherwise, print N lines with a single bead description on each line. Each bead description consists of two integers giving the colors of its two ends. For 1 ≤ i ≤ N1, the second integer on line i must be the same as the first integer on line i + 1. Additionally, the second integer on line N must be equal to the first integer on line 1. Since there are many solutions, any one of them is acceptable. Print a blank line between two successive test cases.

 

Sample Input

2 5 1 2 2 3 3 4 4 5 5 6 5 2 1 2 2 3 4 3 1 2 4

Sample Output

Case #1
some beads may be lost

 

Case #2 

2 1
1 3
3 4
4 2
2 2

 

题解：比较经典的欧拉回路的题目，将颜色看作节点，珠子相当于连接两个颜色的边，由于珠子可以翻转，因此是无向图。

　　　无向图欧拉回路存在的充要条件：连通并且所有点的度数均为偶数。

　　　此题数据直接保证了连通，检查连通性很容易，并查集即可。为了输出一条欧拉回路，采用套圈算法，从任意一个节点出发dfs，走不下去了就回溯，回溯过程　　　　　　　　            中逆向输出节点即可。

 

#include <bits/stdc++.h>

using namespace std;

#define REP(i, n) for (int i = 1; i <= (n); i++)
#define sqr(x) ((x) * (x))

const int maxn = 50 + 10;
const int maxm = 30 + 10;
const int maxs = 10000 + 10;

typedef long long LL;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;

const LL unit = 1LL;
const int INF = 0x3f3f3f3f;
const LL mod = 1000000007;
const double eps = 1e-14;
const double inf = 1e15;
const double pi = acos(-1.0);

int n, iCase;
int deg[maxn], gra[maxn][maxn];

void dfs(int u)
{
    for (int i = 1; i <= 50; i++)
    {
        if (gra[u][i])
        {
            gra[u][i]--;
            gra[i][u]--;
            dfs(i);
            cout << i << " " << u << endl;
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    int T;
    cin >> T;
    while (T--)
    {
        cin >> n;
        cout << "Case #" << ++iCase << endl;
        memset(deg, 0, sizeof(deg));
        memset(gra, 0, sizeof(gra));
        int u, v;
        for (int i = 0; i < n; i++)
        {
            cin >> u >> v;
            gra[u][v]++, gra[v][u]++;
            deg[u]++, deg[v]++;
        }
        bool ok = true;
        for (int i = 1; i <= 50; i++)
        {
            if (deg[i] % 2)
            {
                ok = false;
                break;
            }
        }
        if (!ok)
        {
            cout << "some beads may be lost" << endl;
        }
        else
        {
            dfs(v);
        }
        if (T)
            cout << endl;
    }
    return 0;
}