0、什么是numpy
NumPy是Python中科学计算的基础包。它是一个Python库,提供多维数组对象,各种派生对象(如掩码数组和矩阵),以及用于数组快速操作的各种API,有包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变换、基本线性代数,基本统计运算和随机模拟等等。
NumPy数组 和 原生Python Array(数组)之间有几个重要的区别:
- NumPy 数组在创建时具有固定的大小,与Python的原生数组对象(可以动态增长)不同。更改ndarray的大小将创建一个新数组并删除原来的数组。
- NumPy 数组中的元素都需要具有相同的数据类型,因此在内存中的大小相同。 例外情况:Python的原生数组里包含了NumPy的对象的时候,这种情况下就允许不同大小元素的数组。
- NumPy 数组有助于对大量数据进行高级数学和其他类型的操作。通常,这些操作的执行效率更高,比使用Python原生数组的代码更少。
- 越来越多的基于Python的科学和数学软件包使用NumPy数组; 虽然这些工具通常都支持Python的原生数组作为参数,但它们在处理之前会还是会将输入的数组转换为NumPy的数组,而且也通常输出为NumPy数组。换句话说,为了高效地使用当今科学/数学基于Python的工具(大部分的科学计算工具),你只知道如何使用Python的原生数组类型是不够的 - 还需要知道如何使用 NumPy 数组。
1、为什么要用numpy
1、numpy的高效性
首先,我们尝试一下用python做两个列表的相加

但是当我们希望两个列表的元素逐个相加时,a+b只是对它们进行了一个连接操作,所以这样是不行的,如果我想将它们加在一起,必须写一个for循环,如下所示:

假如你用普通列表,而不希望用numpy包时,这样写是没有问题的,但是在计算方面,它的速度有点慢。下面展示一下这个方法的速度:

每次循环大概是9ms的时间,对于计算机来说,其速度是很慢的。
接下来我们将numpy引入,看看速度和简洁方面有多大的提升

我们可以看到,与python相比,其运行速度相差了一个数量级。 因为python的列表包含的是一堆地址,包含的是自己和相邻元素的地址,你需要全程自己安排每个细节。而numpy是将所有元素组织到一起,存放到一个数据结构中,这些元素在内存中是相邻的,他们都有着相同的类型,因此numpy能对这些数字进行非常快速的运算,因为它不需要进行类型检察,不需要申请获取这些元素。
2、numpy的简洁易读性
这次我不再将数据定义为列表,而是直接将其定义为数组,我们直接进行a+b运算来查看一下结果

通过结果我们可以看到结果的内容前面加了一个array前缀,这是用来与python来进行区分的。同时我们可以看到其进行的操作是直接将数组类的列表对应元素逐个相加。这种点对点的操作,对于几乎所有的操作符都是成立的。

2、numpy的数组
1、查看numpy数组属性
接下来我们介绍一下numpy的数组

前面已经讲过了,前缀array表示数组是基于numpy的.
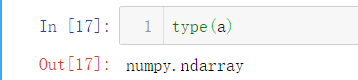
查看类型,这里的nd表示n个维度

查看元素类型,需要说明的是,numpy数组中的每个元素类型是相同的。

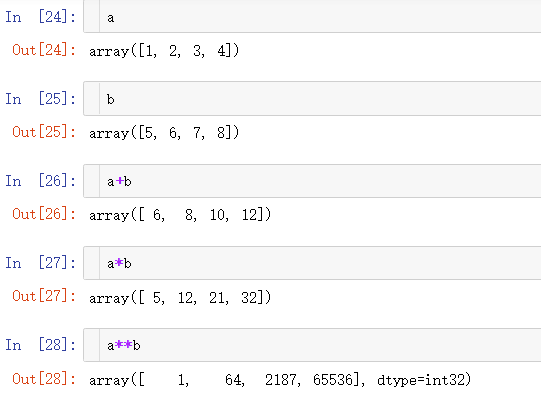
查看数组维度属性。

查看数组的维度。返回的是一个整数元组,指示了一个数组在各个维度的大小。对于一个n行m列的矩阵来说,它的shape是(n,m)。shape的元组长度因此是轴的数量,即ndim,基本上,元组的结果会输出包含和维度数相同个数的元素。
值得一提的是,在type中,元组的意思有人认为是(),其实不然,元组实际上是由()内的逗号决定的,以下为一个示例:

其中括号的存在是为了使其在视觉上更容易作为一个整体组合在一起。
2、numpy数组运算操作
前面已经进行了数组a,b的加减乘除的操作。
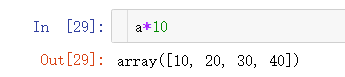
我们可以让数组乘上一个整数,numpy会自动进行广播操作。
在其底层实际上有一个for循环操作,当我们不需要手写for操作,这也是numpy速度快的原因之一。
numpy内部还内置了一些函数,

等等,这些函数是numpy内置的函数,由C完成,执行速度非常快。其类型为ufunc.
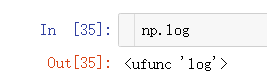
你可以通过打印函数来查看函数本身是基于python还是基于numpy的。

3、修改numpy元素
与数组类似,我们能够修改numpy给定位置的元素。

但是值得注意的是,当原始数组类型为整型时,加入想要修改或填充为一个浮点数,浮点数会被截断。

如果你确实希望将类型转换为浮点型,你可以通过numpy数据类型转换函数astype()进行类型转换

4、numpy高维数组
对于一个高维数组,其创建形式如下所示:

他们在内存中是连续存储的变量表示在数组中的一行。c.size表示的是数组的总大小。
同样的,我们可以类似与数组的方式对二维数组进行操作,不过numpy 不同于pyhton的列表操作.中把所有位置放在同一个括号中。

如果使用未指定索引,numpy会给出未指定维度的所有元素

5、切片操作
切片操作是一种获取数组中子集的方法。切片提供了一个下限表示开始位置,上限表示结束位置,还有一个可选的步长操作。

与python操作不同,上限数是不包含在内的,其显然不是和python的操作完全相同的。
同理,可以对二维数组进行类似的操作。

值得注意的是,对一个数组做切片操作并不是重新创建一个新的区域,而是给一个相同内存缓冲区域的视图。它并不复制数据,只是指向了内存的同一个位置。



假如你确实想复制一个数组,则需使用copy函数的方法进行复制。

6、花式索引
花式索引即按照条件进行索引,而不要求完全相同的步长大小。

对于取区间,直接使用a>30 and a<60是会报错了的。这里需要用到按位与或非的操作符。

同样的,对于两个数组也可以进行同样的花式索引得到条件量。

如果你想知道所有符合条件的位置在哪里,可以使用nozero进行查看。

同样值得注意的是,与切片不同,做花式索引,将会得到一个副本。
7、计算规则
对于numpy而言,运算规则如下所示:
- 首先,计算时,numpy做的第一件事就是检查它们的形状是否匹配。即广播规则。
- 所有的运算规则(+-*/exp,log,.....)都是按照元素逐个运算的。值得注意的是,numpy中*默认数组中按元素乘,矩阵乘积可以用@运算或者dot函数执行。
- 所有的缩减操作,比如求平均,求和等都是应用于某个数组的,除非指出所谓的轴。

- 如果数组中存在者缺损值,例如nan,它会传播。

但是,numpy提供了函数可以对nan进行缺损。
