1、灰度变换的基本概念
灰度变换指对图像的单个像素进行操作,主要以对比度和阈值处理为目的。其变换形式如下:
s=T(r)
其中,T是灰度变换函数;r是变换前的灰度;s是变换后的像素。
图像灰度变换的有以下作用:
- 改善图像的质量,使图像能够显示更多的细节,提高图像的对比度(对比度拉伸)
- 有选择的突出图像感兴趣的特征或者抑制图像中不需要的特征
- 可以有效的改变图像的直方图分布,使像素的分布更为均匀
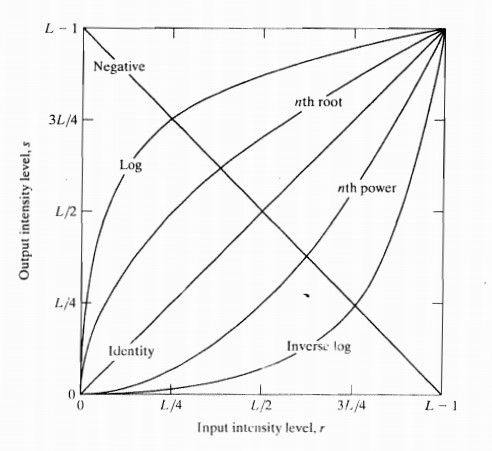
2常用的灰度变换说明
- 线性函数 (图像反转)
- 对数函数:对数和反对数变换
- Gamma变换:n次幂和n次开方变换
- 分段线性变换
3、线性变换
其中,a为直线的斜率,b为在y轴的截距。选择不同的a,b值会有不同的效果:
- a>1,增加图像的对比度
- a<1,减小图像的对比度
- a=0,b!=0,图像变亮或变暗
- a<0且b=0,图像的亮区域变暗,暗区域变亮
- a=-1,b=255,图像亮度反转
OpenCV的实现如下:
灰度图实现:
for (int i = 0; i < srcImg.rows; i++)
{
uchar *srcData = srcImg.ptr<uchar>(i);
for (int j = 0; j < srcImg.cols; j++)
{
dstImg.at<uchar>(i, j) = srcData[j] * k + b;
}
}
彩色图的实现只需拓展到三通道即可:
for (int i = 0; i < RowsNum; i++)
{
for (int j = 0; j < ColsNum; j++)
{
//c为遍历图像的三个通道
for (int c = 0; c < 3; c++)
{
//使用at操作符,防止越界
dstImg.at<Vec3b>(i, j)[c] = saturate_cast<uchar>
(k* (srcImg.at<Vec3b>(i, j)[c]) + b);
}
}
}
示例:
#include "stdafx.h"
#include <iostream>
#include <opencv2corecore.hpp>
#include <opencv2highguihighgui.hpp>
#include <opencv2imgprocimgproc.hpp>
using namespace std;
using namespace cv;
int main()
{
Mat srcImg = imread("rice.png",0);
if (!srcImg.data)
{
cout << "读入图片失败" << endl;
return -1;
}
double k, b;
cout << "请输入k和b值:";
cin >> k >> b;
int RowsNum = srcImg.rows;
int ColsNum = srcImg.cols;
Mat dstImg(srcImg.size(), srcImg.type());
//进行遍历图像像素,对每个像素进行相应的线性变换
for (int i = 0; i < srcImg.rows; i++)
{
uchar *srcData = srcImg.ptr<uchar>(i);
for (int j = 0; j < srcImg.cols; j++)
{
dstImg.at<uchar>(i, j) = srcData[j] * k + b;
}
}
imshow("原图", srcImg);
imshow("线性变换后的图像", dstImg);
waitKey();
return 0;
}
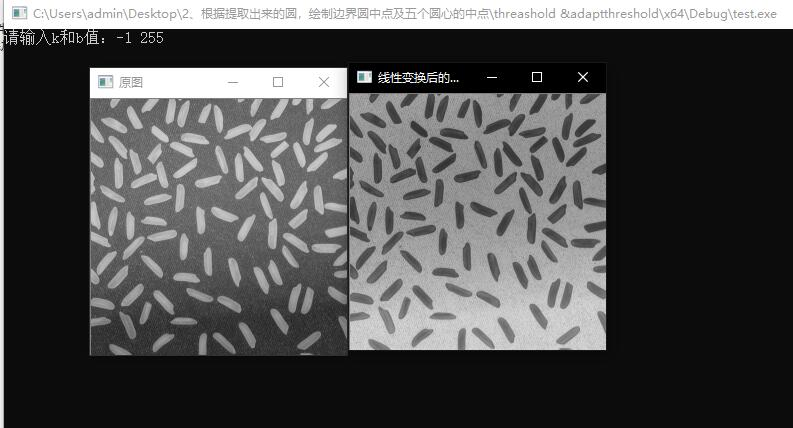
程序运行结果如下:
4、对数变换
对数变换的通用公式是:
s=log(1+r)/b
其中,b是一个常数,用来控制曲线的弯曲程度,其中,b越小越靠近y轴,b越大越靠近x轴。表达式中的r是原始图像中的像素值,s是变换后的像素值,可以分析出,当函数自变量较低时,曲线的斜率很大,而自变量较高时,曲线的斜率变得很小。 正是因为对数变
换具有这种压缩数据的性质,使得它能够实现图像灰度拓展和压缩的功能。即对数变换可以拓展低灰度值而压缩高灰度级值,让图像的灰度分布更加符合人眼的视觉特征。
假设r≥0,根据上图中的对数函数的曲线可以看出:对数变换,将源图像中范围较窄的低灰度值映射到范围较宽的灰度区间,同时将范围较宽的高灰度值区间映射为较窄的灰度区间,从而扩展了暗像的值,压缩了高灰度的值,能够对图像中低灰度细节进行增
强。;从函数曲线也可以看出,反对数函数的曲线和对数的曲线是对称的,在应用到图像变换其结果是相反的,反对数变换的作用是压缩灰度值较低的区间,扩展高灰度值的区间。
通过OpenCV实现程序有三种,这里就不一一列举了,在示例中给出:
示例:
#include "stdafx.h"
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <iostream>
using namespace cv;
// 对数变换方法1
cv::Mat logTransform1(cv::Mat srcImage, int c)
{
// 输入图像判断
if (srcImage.empty())
std::cout << "No data!" << std::endl;
cv::Mat resultImage =
cv::Mat::zeros(srcImage.size(), srcImage.type());
// 计算 1 + r
cv::add(srcImage, cv::Scalar(1.0), srcImage);
// 转换为32位浮点数
srcImage.convertTo(srcImage, CV_32F);
// 计算 log(1 + r)
log(srcImage, resultImage);
resultImage = c * resultImage;
// 归一化处理
cv::normalize(resultImage, resultImage,
0, 255, cv::NORM_MINMAX);
cv::convertScaleAbs(resultImage, resultImage);
return resultImage;
}
// 对数变换方法2
cv::Mat logTransform2(Mat srcImage, float c)
{
// 输入图像判断
if (srcImage.empty())
std::cout << "No data!" << std::endl;
cv::Mat resultImage =
cv::Mat::zeros(srcImage.size(), srcImage.type());
double gray = 0;
// 图像遍历分别计算每个像素点的对数变换
for (int i = 0; i < srcImage.rows; i++) {
for (int j = 0; j < srcImage.cols; j++) {
gray = (double)srcImage.at<uchar>(i, j);
gray = c * log((double)(1 + gray));
resultImage.at<uchar>(i, j) = saturate_cast<uchar>(gray);
}
}
// 归一化处理
cv::normalize(resultImage, resultImage,
0, 255, cv::NORM_MINMAX);
cv::convertScaleAbs(resultImage, resultImage);
return resultImage;
}
// 对数变换方法3
cv::Mat logTransform3(Mat srcImage, float c)
{
// 输入图像判断
if (srcImage.empty())
std::cout << "No data!" << std::endl;
cv::Mat resultImage =
cv::Mat::zeros(srcImage.size(), srcImage.type());
srcImage.convertTo(resultImage, CV_32F);
resultImage = resultImage + 1;
cv::log(resultImage, resultImage);
resultImage = c * resultImage;
cv::normalize(resultImage, resultImage, 0, 255, cv::NORM_MINMAX);
cv::convertScaleAbs(resultImage, resultImage);
return resultImage;
}
int main()
{
// 读取灰度图像及验证
cv::Mat srcImage = cv::imread("111.jpg", 0);
if (!srcImage.data)
return -1;
// 验证三种不同方式的对数变换速度
cv::imshow("srcImage", srcImage);
float c = 2;
cv::Mat resultImage;
double tTime;
tTime = (double)getTickCount();
const int nTimes = 10;
for (int i = 0; i < nTimes; i++)
{
resultImage = logTransform3(srcImage, c);
}
tTime = 1000 * ((double)getTickCount() - tTime) /
getTickFrequency();
tTime /= nTimes;
std::cout << "第三种方法耗时:" << tTime << std::endl;
cv::imshow("resultImage", resultImage);
cv::waitKey(0);
return 0;
}
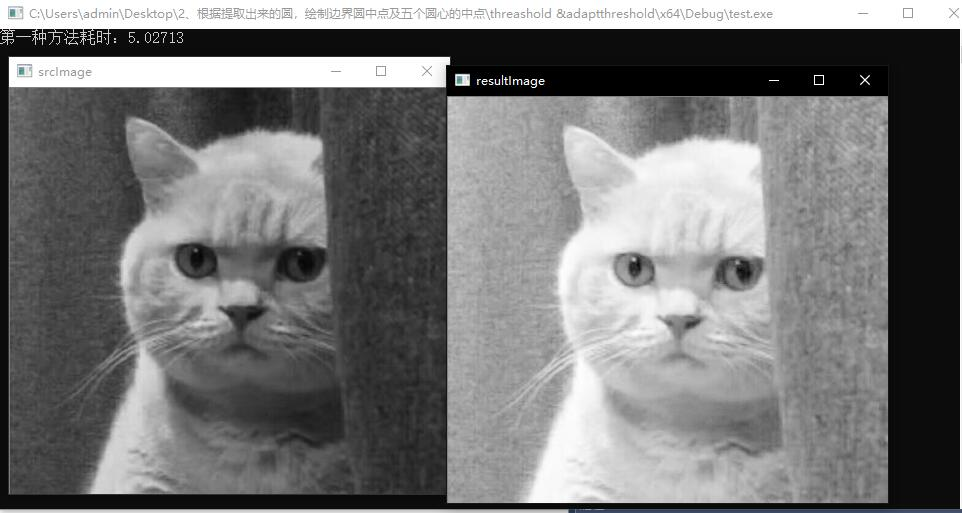
三种方法运行效果分别如下:

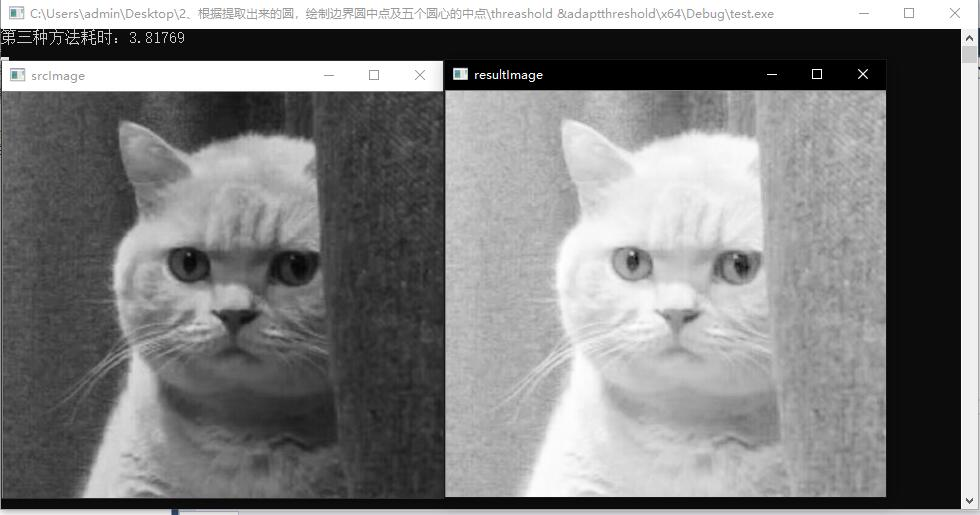
5、伽马变换
基于幂次变换的Gamma校正是图像处理中一种非常重要的非线性变换,它与对数变换相反,它是对输入图像的灰度值进行指数变换,进而校正亮度上的偏差。通常Gamma校正长应用于拓展暗调的细节。伽马变换的公式为:
s=crγ
其中c和 γ为正常数.,伽马变换的效果与对数变换有点类似,当 γ >1时将较窄范围的低灰度值映射为较宽范围的灰度值,同时将较宽范围的高灰度值映射为较窄范围的灰度值;当 γ <1时,情况相反,与反对数变换类似。其函数曲线如下:
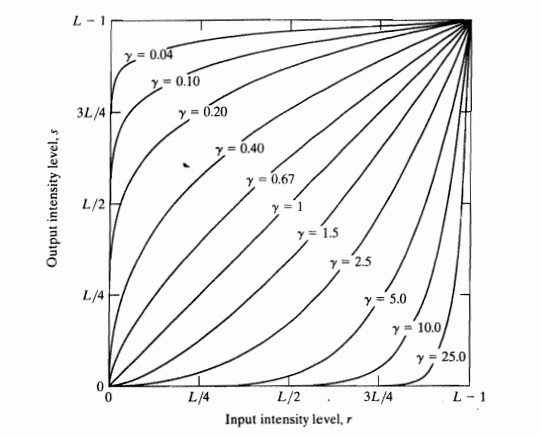
当γ<1时,图像的高光部分被扩展而暗调备份被压缩,γ的值越小,对图像低灰度值的扩展越明显;当γ>1时,图像的高光部分被压缩而暗调部分被扩展,γ的值越大,对图像高灰度值部分的扩展越明显。这样就能够显示更多的图像的低灰度或者高灰度细节。
- 当γ<1时,低灰度区域动态范围扩大,进而图像对比度增强,高灰度值区域动态范围减小,图像对比度降低,图像整体灰度值增大,此时与图像的对数变换类似。
- γ>1时,低灰度区域的动态范围减小进而对比度降低,高灰度区域动态范围扩大,图像的对比度提升,图像的整体灰度值变小,Gamma校正主要应用在图像增强。
总之,r<1的幂函数的作用是提高图像暗区域中的对比度,而降低亮区域的对比度;r>1的幂函数的作用是提高图像中亮区域的对比度,降低图像中按区域的对比度。所以Gamma变换主要用于图像的校正,对于灰度级整体偏暗的图像,可以使用r<1的幂函数增大动态范围。对于灰度级整体偏亮的图像,可以使用r>1的幂函数增大灰度动态范围。
基于OpenCV的实现:
Mat GammaTrans(Mat &srcImag, float parameter)
{
//建立查表文件LUT
unsigned char LUT[256];
for (int i = 0; i < 256; i++)
{
//Gamma变换定义
LUT[i] = saturate_cast<uchar>(pow((float)(i / 255.0), parameter)*255.0f);
}
Mat dstImage = srcImag.clone();
//输入图像为单通道时,直接进行Gamma变换
if (srcImag.channels() == 1)
{
MatIterator_<uchar>iterator = dstImage.begin<uchar>();
MatIterator_<uchar>iteratorEnd = dstImage.end<uchar>();
for (; iterator != iteratorEnd; iterator++)
*iterator = LUT[(*iterator)];
}
else
{
//输入通道为3通道时,需要对每个通道分别进行变换
MatIterator_<Vec3b>iterator = dstImage.begin<Vec3b>();
MatIterator_<Vec3b>iteratorEnd = dstImage.end<Vec3b>();
//通过查表进行转换
for (; iterator!=iteratorEnd; iterator++)
{
(*iterator)[0] = LUT[((*iterator)[0])];
(*iterator)[1] = LUT[((*iterator)[1])];
(*iterator)[2] = LUT[((*iterator)[2])];
}
}
return dstImage;
}
示例:
#include "stdafx.h"
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/imgproc/types_c.h>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/highgui/highgui_c.h>
#include <iostream>
using namespace cv;
using namespace std;
void MyGammaCorrection(Mat& src, Mat& dst, float fGamma)
{
// build look up table
unsigned char lut[256];
for (int i = 0; i < 256; i++)
{
lut[i] = saturate_cast<uchar>(pow((float)(i / 255.0), fGamma) * 255.0f);
}
dst = src.clone();
const int channels = dst.channels();
switch (channels)
{
case 1: //灰度图的情况
{
MatIterator_<uchar> it, end;
for (it = dst.begin<uchar>(), end = dst.end<uchar>(); it != end; it++)
//*it = pow((float)(((*it))/255.0), fGamma) * 255.0;
*it = lut[(*it)];
break;
}
case 3: //彩色图的情况
{
MatIterator_<Vec3b> it, end;
for (it = dst.begin<Vec3b>(), end = dst.end<Vec3b>(); it != end; it++)
{
//(*it)[0] = pow((float)(((*it)[0])/255.0), fGamma) * 255.0;
//(*it)[1] = pow((float)(((*it)[1])/255.0), fGamma) * 255.0;
//(*it)[2] = pow((float)(((*it)[2])/255.0), fGamma) * 255.0;
(*it)[0] = lut[((*it)[0])];
(*it)[1] = lut[((*it)[1])];
(*it)[2] = lut[((*it)[2])];
}
break;
}
}
}
int main()
{
Mat image = imread("111.jpg");
if (image.empty())
{
cout << "Error: Could not load image" << endl;
return 0;
}
Mat dst;
float fGamma = 1 / 2.2;
MyGammaCorrection(image, dst, fGamma);
imshow("Source Image", image);
imshow("Dst", dst);
waitKey();
return 0;
}
程序运行结果如下:
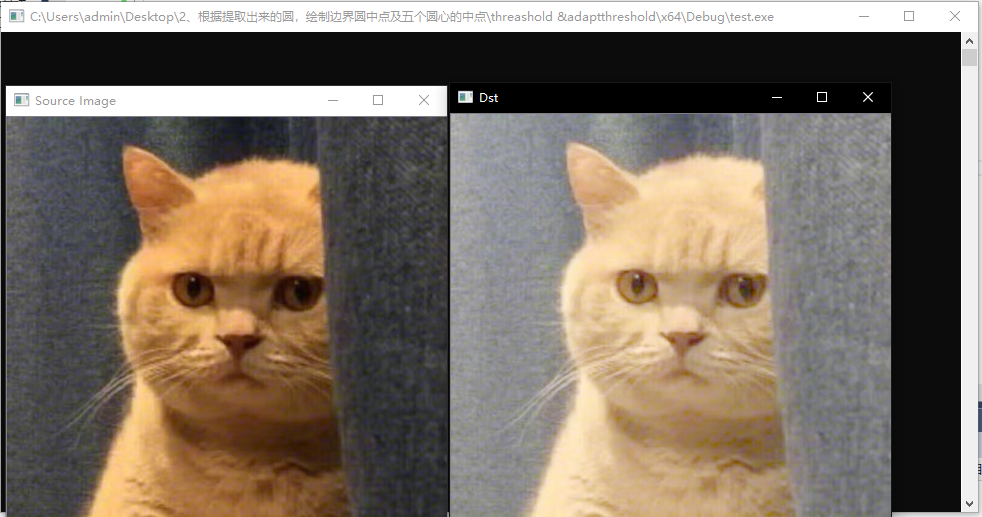
6 分段线性变换
6.1、对比度拉伸技术
图像的对比度拉伸是通过扩展图像灰度级动态范围来实现的,它可以扩展对应的全部灰度范围。图像的低对比度一般是由于图像图像成像亮度不够、成像元器件参数限制或设置不当造成的。提高图像的对比度可以增强图像各个区域的对比效果,对图像中感兴趣的区域进行增强,而对图像中不感兴趣的区域进行相应的抑制作用。对比度拉伸是图像增强中的重要的技术之一。这里设点(x1,y1)与(x2,y2)是分段线性函数中折点位置坐标。常见的三段式分段线性变换函数的公式如下:
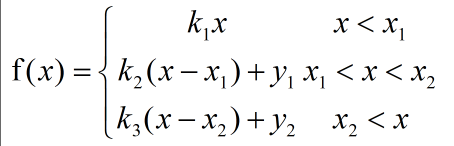
其中

其图像如下:
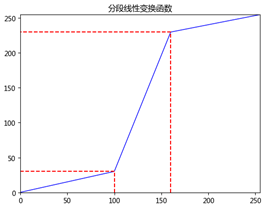
需要注意的是,分段线性一般要求函数是单调递增的,目的是防止图像中的灰度级不满足一一映射。
示例:
#include "stdafx.h"
#include <iostream>
#include <opencv2corecore.hpp>
#include <opencv2highguihighgui.hpp>
#include <opencv2imgprocimgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("111.jpg", 0);
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return -1;
}
imshow("原始图片", srcImage);
Mat dstImage(srcImage);
int rowsNum = dstImage.rows;
int colsNum = dstImage.cols;
//图像连续性判断
if (dstImage.isContinuous())
{
colsNum = colsNum * rowsNum;
rowsNum = 1;
}
//图像指针操作
uchar *pDataMat;
int pixMax = 0, pixMin = 255;
//计算图像像素的最大值和最小值
for (int j = 0; j < rowsNum; j++)
{
pDataMat = dstImage.ptr<uchar>(j);
for (int i = 0; i < colsNum; i++)
{
if (pDataMat[i] > pixMax)
pixMax = pDataMat[i];
if (pDataMat[i] < pixMin)
pixMin = pDataMat[i];
}
}
//进行对比度拉伸
for (int j = 0; j < rowsNum; j++)
{
pDataMat = dstImage.ptr<uchar>(j);
for (int i = 0; i < colsNum; i++)
{
pDataMat[i] = (pDataMat[i] - pixMin) * 255 / (pixMax - pixMin);
}
}
imshow("对比度拉伸后的图像", dstImage);
waitKey();
return 0;
}
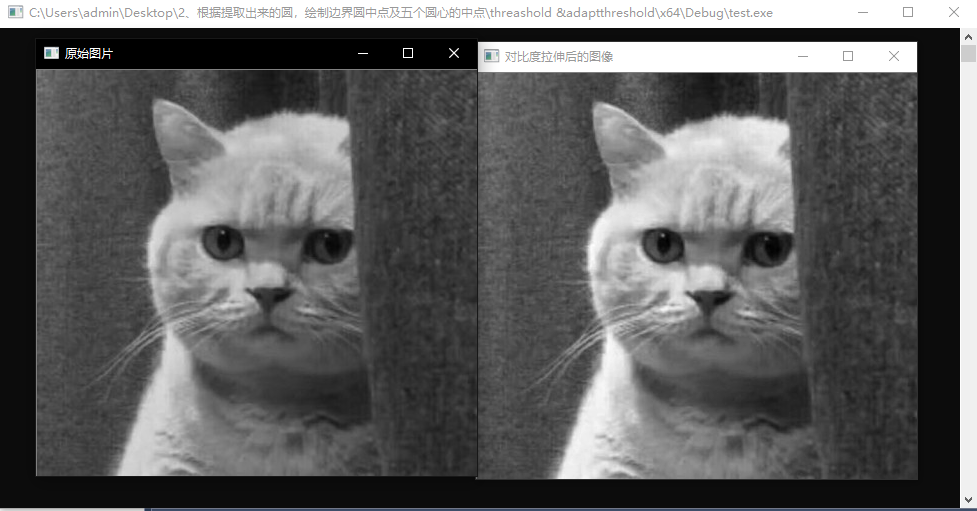
6.2、 灰度级分层
灰度级分层的处理可以突出特定灰度范围的亮度,可以应用于增强某些特征。
- 将感兴趣范围内的所有灰度值显示位一个值(如白色),而将其他灰度值显示为另外一个值(如黑色)。如下图左图所示,最后将产生一副二值图像
- 仅仅改变感兴趣范围的灰度值,使其显示为一个值,如下图右图所示。(这种方法一般用的少,这里就不详细介绍了)
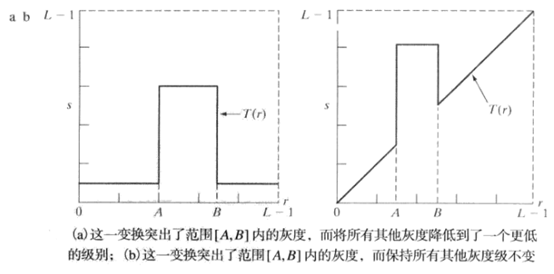
下面使用OpenCV对灰度级分层进行一个实现
示例:
#include "stdafx.h"
#include <iostream>
#include <opencv2corecore.hpp>
#include <opencv2highguihighgui.hpp>
#include <opencv2imgprocimgproc.hpp>
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("111.jpg", 0);
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return 0;
}
imshow("原图像", srcImage);
Mat dstImage = srcImage.clone();
int rowsNum = dstImage.rows;
int colsNum = dstImage.cols;
//图像连续性判断
if (dstImage.isContinuous())
{
colsNum *= rowsNum;
rowsNum = 1;
}
//图像指针操作
uchar *pDataMat;
int controlMin = 50;
int controlMax = 150;
//计算图像的灰度级分层
for (int j = 0; j < rowsNum; j++)
{
pDataMat = dstImage.ptr<uchar>(j);
for (int i = 0; i < colsNum; i++)
{
//第一种方法,二值映射
if (pDataMat[i] > controlMin)
pDataMat[i] = 255;
else
pDataMat[i] = 0;
//第二种方法:区域映射
//if (pDataMat[i] > controlMax && pDataMat[j] < controlMin)
// pDataMat[i] = controlMax;
}
}
imshow("灰度分层后的图像", dstImage);
waitKey();
return 0;
}
运行结果如下所示:
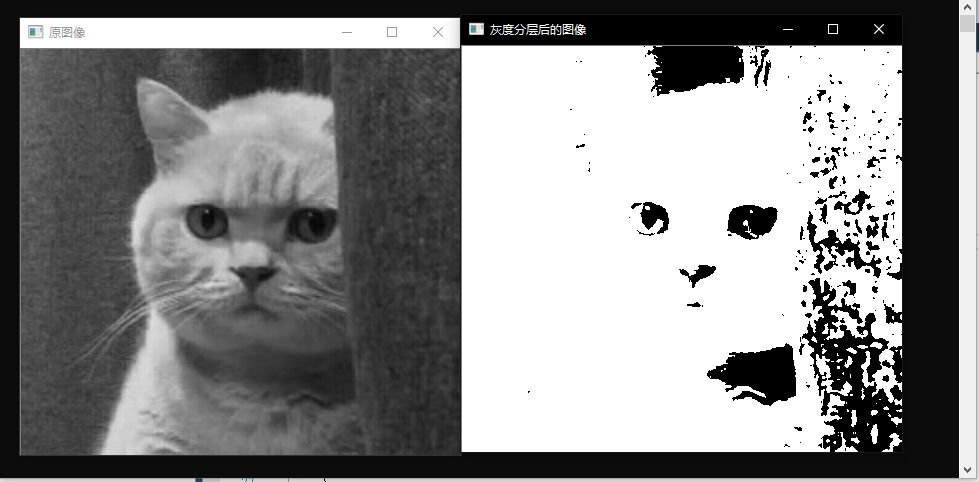
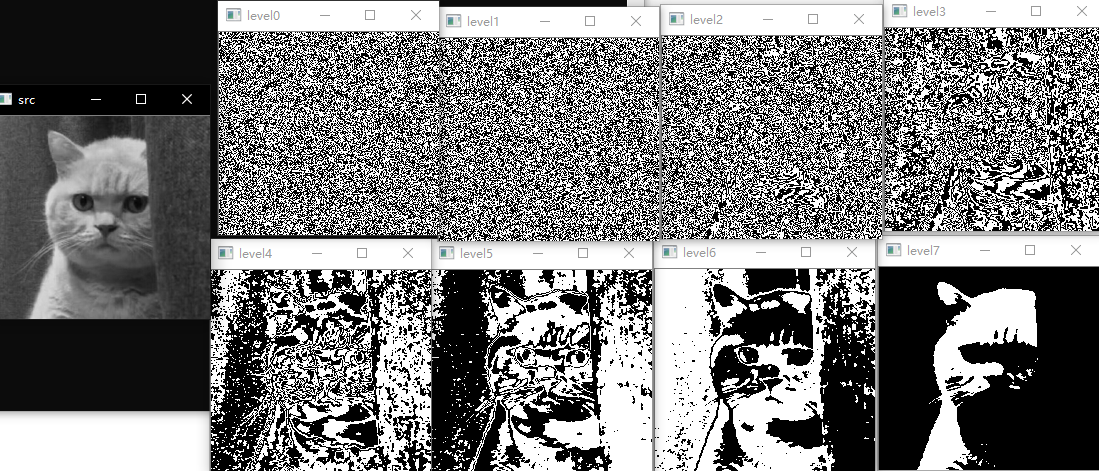
6.2、比特平面分层
像素是由比特组成的竖直。例如,在256级灰度图像中,每个像素的灰度是由8bit组成,替代突出灰度级范围,我们可以突出比特来突出整个图像的外观。一副8比特灰度图可考虑分层1到8个比特平面。很容易理解的是,4个高阶比特平面,特别是最后两个比特平面,包含了在视觉上很重要的大多数数据。而低阶比特平面则在图像上贡献了更精细的灰度细节。

示例:
#include "stdafx.h"
#include<opencv2/highgui/highgui.hpp>
#include<opencv2/imgproc/imgproc.hpp>
#include<iostream>
using namespace std;
using namespace cv;
int b[8];
void binary(int num)
{
for (int i = 0; i < 8; i++)
b[i] = 0;
int i = 0;
while (num != 0)
{
b[i] = num % 2;
num = num / 2;
i++;
}
}
int main()
{
Mat srcImage = imread("111.jpg", 0);
resize(srcImage, srcImage, cv::Size(), 0.5, 0.5);
Mat d[8];
for (int k = 0; k < 8; k++)
d[k].create(srcImage.size(), CV_8UC1);
int rowNumber = srcImage.rows, colNumber = srcImage.cols;
for (int i = 0; i < rowNumber; i++)
for (int j = 0; j < colNumber; j++) {
int num = srcImage.at<uchar>(i, j);
binary(num);
for (int k = 0; k < 8; k++)
d[k].at<uchar>(i, j) = b[k] * 255;
}
imshow("src", srcImage);
for (int k = 0; k < 8; k++) {
imshow("level" + std::to_string(k), d[k]);
}
waitKey(0);
return 0;
}