懵逼乌斯反演果然名不虚传,自闭了两天的我打算学习一下这一块比较实用的数论内容。
(注:1.为了区分狄尼克雷卷积与乘法,本篇文章中乘号全部省略,卷积全部用" * "表示。2.用gcd(a,b)表示a和b的最大公约数。3.用lcm(a,b)表示a和b的最小公倍数。4.用C(n,m)表示在n个数中选择m个数的方案数。5." ^ "在本篇文章中表示乘方而不是异或。)
知识点:
一、数论函数:
定义:定义域为正整数,(陪域为复数)的函数。
二、积性函数
1.定义:满足f(ab)=f(a)f(b)(gcd(a,b)=1)的数论函数。
*完全积性函数定义:满足f(ab)=f(a)f(b)的数论函数。
2.常见积性函数:(1)欧拉函数φ(n)(2)莫比乌斯函数μ(n)(3)除数函数dk(n)表示n的所有正因子k次幂和
3.积性函数性质:
(1)设n=∏pici ,则f(n)=∏f(pici),由定义显然。因此大多数积性函数可以线性筛预处理。
(2)若f(n),g(n)均为积性函数,h(n)=f(n)g(n),h(n)=f(n)/g(n)也为积性函数。
证明:h(a)h(b)=f(a)g(a)f(b)g(b)=f(a)f(b)g(a)g(b)=f(ab)g(ab)=h(ab),满足定义,得证。
(3)欧拉函数φ(n)的性质:(φ*1)(n)=n。
证明:
(φ*1)(n)=∑d|n φ(d)1(n/d)=∑d|n φ(d),
分解质因数得n=∏(i:1~k)pici ,
由于欧拉函数为积性函数,∑d|n φ(d)=∏(i:1~k)(∑(j:0~ci)φ(pij)),(将式子拆开显然)
由φ(1)=1得 ∑d|n φ(d)=∏(i:1~k)(∑(j:1~ci)φ(pij)+1)
由φ(pe)=(p-1)pe-1 =pe -pe-1 ,可得∑d|n φ(d)=∏(i:1~k)(∑(j:1~ci)(pij - pij-1)+1)
将∑内的式子拆开得,∑d|n φ(d)=∏pici =n。
三、狄尼克雷卷积
1.定义:两个数论函数的狄尼克雷卷积 (f*g)(n)=∑d|n f(d)g(n/d)。
2.性质:
(1)满足交换律。
感性证明:每一个数的因子都是两两对应的,所以无论是什么顺序,都会将所有的f(d)和g(n/d)的乘积都加一遍。
(2)满足结合律。
证明如图:

(3)满足分配律。
证明:设k(n)=g(n)+h(n),f*(g+h)(n)=(f*k)(n)=∑d|n f(n)k(n/d)=∑d|n f(n)(g(n/d)+h(n/d))=∑d|n f(n)g(n/d)+∑d|n f(n)h(n/d)=(f*g)(n)+(f*h)(n),得证。
(4)积性函数的卷积还是积性函数。
证明如图:
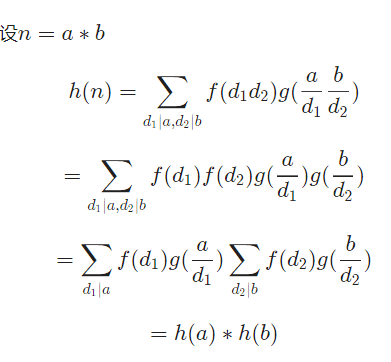
3.单位元:e(n),e(1)=1,e(n)=0(n!=1)。(单位元:若对于任意的数论函数f(n),都有(f*e)(n)=f(n),则e(n)称为单位元。)
证明:(f*e)(n)=∑d|n f(d)e(n/d),当且仅当d==n时,e(n/d=1)=1,因此只会在d==n时对答案有贡献,贡献为f(n),因此(f*e)(n)=f(n),得证。
四、莫比乌斯函数
(1)定义:μ(1)=1;当n含平方因子时,μ(n)=0;否则μ(n)=(-1)^k,k为n的本质不同的质因子个数。
(2)定义狄尼克雷卷积的单位元为e(n),e(n)=∑d|n μ(d)。
e(n)=∑d|n μ(d),
将n分解质因数得:n=∏(i:1~k)pici ,令n'=∏(i:1~k)pi ,由μ的定义可知,μ(n)的大小只与n本质不同的质因子有关,得:
e(n)=∑d|n' μ(d),
枚举d为i个质因子的乘积,在k个质因子中选择i的方案数为C(k,i),得:
e(n) = ∑(i:0~k) C(k,i)μ(i)
= ∑(i:0~k) C(k,i)(-1)^i
= ∑(i:0~k) C(k,i)(-1)^i 1^(k-i)
根据二项式定理,原式=((-1)+1)^k,当k==0即n==1时e(n)=1,否则e(n)=0。
五、莫比乌斯反演
设f(n),g(n)为两个数论函数,
如果有f(n)=(g*1)(n),
那么有g(n)=(f*μ)(n)。
证明:
将一式带入二式得,g(n)=(f*μ)(n)=(g*1*μ)(n),
根据卷积的结合律得,g(n)=(g*(μ*1))(n),
(μ*1)(n)=∑d|n μ(d)=e(n),
带入上式得,g(n)=(g*e)(n)=g(n),成立。
六、线性筛
前文已经提到,绝大多数积性函数可以用线性筛筛出来,下面附上线性筛筛素数,欧拉函数,莫比乌斯函数的代码:
int n,prime[N],num=0,phi[N],miu[N];
bool notprime[N];
void get()
{
notprime[1]=1;
phi[1]=1;
miu[1]=1;
for(int i=2;i<=n;i++)
{
if(!notprime[i]){
prime[++num]=i;
phi[i]=i-1;
//φ(p)=p-1
miu[i]=-1;
//质数本质不同的质因子只有自己,因此μ(p)=(-1)^1=-1
}
for(int j=1;j<=num;j++)
{
if(i*prime[j]>n)break;
notprime[i*prime[j]]=1;
//每个素数只会被自己的最小质因子筛一次
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
miu[i*prime[j]]=0;
//i*prime[j]含有平方因子prime[j]^2,因此μ(i*prime[j])=0
break;//确保每个数只会被最小质因子筛一次
}
else {
phi[i*prime[j]]=phi[i]*phi[prime[j]];
miu[i*prime[j]]=miu[i]*miu[prime[j]];
//μ(n),φ(n)均满足积性函数性质
}
}
}
}
七、杜教筛
1.作用:O(n^(2/3))地求数论函数的前缀和。
2.推导:
设f(n)为一数论函数,
我们要求S(n)=∑(i:1~n)f(i),
我们找到另一个积性数论函数g(n),则
∑(i:1~n) (f*g)(n)=∑(i:1~n)∑d|i g(d)f(i/d)
把d提出来得,∑(i:1~n) (f*g)(n)=∑(d:1~n)g(d)∑d|i f(i/d)
=∑(i:1~n)g(i)∑(j:1~(n/i))f(j)=∑(i:1~n)g(i)S(n/d)
根据前缀和思想,g(1)S(n)=∑(i:1~n)g(i)S(n/i)-∑(i:2~n)g(i)S(n/i)
=∑(i:1~n)(g*f)(i)-∑(i:2~n)g(i)S(n/i)
未完