题目
A题意:给出两个数a、b,两种操作a+=b , b+=a , 问最少几次操作使得max(a,b) > n.
解法:假定a>b,一直进行,a为a+b的和,b为原来的a,这样形成的是裴波纳妾数列。
void solve(){
int a , b , n , cnt = 0;
cin >> a >> b >> n;
if(a < b)swap(a , b);
while(a <= n){
int t = a ;
a += b ;
b = t ;
cnt++;
}
cout << cnt << endl;
}
B题意:要求求最短的字符串包含最少k个codeforces子序列。
解法:按codeforces相对顺序依次增加直到大于k个子序列。子序列个数等于(n_1*n_2*...n_{10})(n_i为各字母数量)
int a[11];
char s[12] = "0codeforces";
void solve(){
int k ;
cin >> k ;
rep(i , 1 , 10){
a[i] = 1 ;
}
int sum = 1 ;
while(sum < k){
rep(i , 1 , 10){
sum /= a[i];
a[i]++;
sum *= a[i];
if(sum >= k) break;
}
}
rep(i , 1 , 10){
while(a[i]--){
cout << s[i] ;
}
}
cout << endl;
}
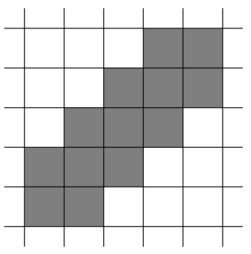
C题意:在一个白色方格坐标中,选择黑色方格,要满足三个条件:1、所有黑色方格联通,2、每个黑色方格只能有偶数个黑色方格作相邻,3、只有k个黑色方格与四个黑色方格相邻。输出满足条件的所有黑色方格的坐标。
解法:构造
void solve(){
int n ;
cin >> n ;
vector<pii>v;
v.pb(mp(0 , 0)) , v.pb(mp(1 , 0));
v.pb(mp(0 , 1)) , v.pb(mp(1 , 1));
rep(i , 1 , n){
v.pb(mp(i+1 , i));
v.pb(mp(i , i+1));
v.pb(mp(i+1 , i+1));
}
cout << size(v) << endl;
for(auto i : v){
cout << i.fi << " " << i.se << endl;
}
}
D题意:n个非负整数,可以选任意两个数进行任意次操作:(设a_i = x , a_j = y,那么 a_i = x&y , a_j = x|y),问操作完后所有数平方和最大为多少。
解法:可以直到,这种操作就是在对两个数二进制下1的重组,比如100,001 , 重组最大为101,000.
1的总数不变,统计1的数量,贪心构造尽可能使一个数大。
int cnt[29];
void solve(){
int n ;
cin >> n ;
rep(i , 1 , n){
int x ;
cin >> x;
rep(j , 0 , 20){
if(x&(1<<j)){
cnt[j]++;
}
}
}
int ans = 0 ;
rep(i , 1 , n){
int cur = 0 ;
rep(j , 0 , 20){
if(cnt[j]){
cur += (1<<j);
cnt[j]--;
}
}
ans += cur*cur ;
}
cout << ans << endl;
}